Существование плоскости, параллельной данной плоскости

ПАРАЛЛЕЛЬНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Параллельные прямые в пространстве

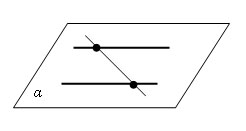
Две прямые в пространстве называются параллельными, если они лежат в одной плоскости и не пересекаются.

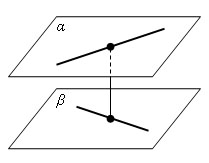
Прямые, которые не пересекаются и не лежат в одной плоскости, называются скрещивающимися.

Параллельные прямые в пространстве. Свойства Теорема Через точку вне данной прямой можно провести прямую, параллельную этой прямой, и притом только одну. 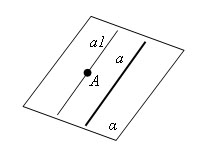Доказательство Пусть a – данная прямая и A – точка, не лежащая на этой прямой. Проведем через прямую a и точку A плоскость α. Проведем через точку A в плоскости α прямую a1, параллельную a. Докажем, что прямая a1, параллельная a, единственна. Допустим, что существует другая прямая a2, проходящая через точку A и параллельная прямой a. Через прямые a и a2 можно провести плоскость α2. Плоскость α2 проходит через прямую a и точку A; следовательно, по теореме о точке и прямой в пространстве она совпадает с α. Теперь по аксиоме параллельных прямые a1 и a2 совпадают. Теорема доказана.

Признак параллельности прямых в пространстве

Теорема

Две прямые, параллельные третьей прямой, параллельны.

Доказательство

Пусть прямые b и с параллельны прямой a. Нужно доказать, что прямые b и с параллельны.
Случай, когда прямые a, b, с лежат в одной плоскости рассмотрен а разделе параллельные прямые.
Пусть прямые не лежат в одной плоскости и β - плоскость, в которой лежат прямые a и b, а γ - плоскость, в которой лежат прямые a и с. Плоскости β и γ различны. Отметим на прямой b какую-нибудь точку B и проведем плоскость γ1 через прямую с и точку B. Она пересечет плоскость β по прямой b1.
Прямой b1 не пересекает плоскость γ. Действительно, точка пересечения должна принадлежать прямой a, так как прямая b1 лежит в плоскости β. С другой стороны, она должна лежать и на прямой с, так как прямая b1 лежит в плоскости γ1. Но прямые a и с как параллельные не пересекаются.
Так как прямая b1 лежит в плоскости β и не пересекает прямую a, то она параллельна a, а значит, совпадает с b по аксиоме параллельных. Значит, прямая b, совпадая с прямой b1, лежит в одной плоскости с прямой с (в плоскости γ1) и не пересекает ее и прямые b и с параллельны. Теорема доказана.

Признак параллельности прямой и плоскости Теорема Если прямая, не принадлежащая плоскости, параллельна какой-нибудь прямой в этой плоскости, то она параллельна и самой плоскости. Доказательство Пусть α - плоскость, a – не лежащая в ней прямая и a1 – прямая в плоскости α, параллельная прямой a. Проведем плоскость α1 через прямые a и a1. Плоскости α и α1 пересекаются по прямой a1. Если бы прямая a пересекала плоскость α, то точка пересечения принадлежала бы прямой a1. Но это невозможно, так как прямые a и a1 параллельны. Следовательно, прямая a не пересекает плоскостью α, а значит, параллельна плоскости α. Теорема доказана.

Признак параллельности плоскостей Две плоскости называются параллельными, если они не пересекаются. Теорема Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны. Доказательство Пусть α и β - данные плоскости, a1 и a2 – прямые в плоскости α, пересекающиеся в точке A, b1 и b2 – соответственно параллельные им прямые в плоскости β. Предположим, что плоскости α и β не параллельны, а значит пересекаются по некоторой прямой с. По теореме о признаке параллельности прямой и плоскости прямые a1 и a2, как параллельные прямые b1 и b2, параллельны плоскости β, и поэтому они не пересекают лежащую в этой плоскости прямую с. Таким образом, в плоскости α через точку A проходят прямые a1 и a2, параллельные прямой с. Это невозможно по аксиоме параллельных. Что противоречит предположению. Теорема доказана.

Существование плоскости, параллельной данной плоскости

Теорема

Через точку вне данной плоскости можно провести плоскость, параллельную данной, и притом только одну.

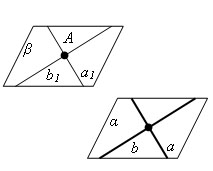
Доказательство

Проведем в данной плоскости α какие-нибудь две пересекающиеся прямые a и b. Через данную точку A проведем параллельные им прямые a1 и b1. Плоскость β, проходящая через прямые a1 и b1, по теореме о признаке параллельности плоскостей параллельна плоскости α.

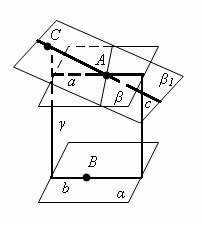
Предположим, что через точку A проходит другая плоскость β1, тоже параллельная плоскости α. Отметим на плоскости β1 какую-нибудь точку С, не лежащую в плоскости β. Проведем плоскость γ через точки A, С и какую-нибудь точку B плоскости α. Эта плоскость пересечет плоскости α, β и β1 по прямым b, a и с. Прямые a и с не пересекают прямую b, так как не пересекают плоскость α. Следовательно, они параллельны прямой b. Но в плоскости γ через точку A может проходить только одна прямая, параллельная прямой b. что противоречит предположению. Теорема доказана.

Свойства параллельных плоскостей Теорема Если две параллельные плоскости пересекаются третьей, то прямые пересечения параллельны. Доказательство Согласно определению параллельные прямые – это прямые, которые лежат в одной плоскости и не пересекаются. Прямые лежат в одной плоскости – секущей плоскости. Они не пересекаются, так как не пересекаются содержащие их параллельные плоскости. Следовательно, прямые параллельны. Теорема доказана.

Свойства параллельных плоскостей, равенство отрезков Теорема Отрезки параллельных прямых, заключенные между двумя параллельными плоскостями, равны.. Доказательство Пусть α1 и α2 – параллельные плоскости, a и b – пересекающие их параллельные прямые, A1, A2 и B1, B2 – точки пересечения прямых с плоскостями. Проведем через прямые a и b плоскость. Она пересекает плоскости α1 и α2 по параллельным прямым A1B1 и A2B2. Четырехугольник A1B1B2A2 – параллелограмм, так как у него противолежащие стороны параллельны. А у параллелограмма противолежащие стороны равны. Значит, A1A2 = B1B2. Теорема доказана.