Лекция №2
Длина вектора и способы ее вычисления в ортонормированном базисе. Скалярное произведение векторов и его свойства. Понятие об ориентации плоскости и пространства. Угол между векторами и способы его вычисления.
Цели: ввести понятие ортонормированного базиса, скалярного произведения двух векторов; рассмотреть длину вектора в ортонормированном базисе; определить способы нахождения угла между векторами в произвольном базисе и в ортонормированном базисе; рассмотреть геометрический и физический смысл скалярного произведения.
План лекции:
1. Понятие ортонормированного базиса.
2. Длина вектора в ортонормированном базисе.
3. Понятие угла между векторами и способы его нахождения.
4. Понятие скалярного произведения двух векторов и его свойства.
5. Скалярное произведение в ортонормированном базисе.
6. Геометрический и физический смысл скалярного произведения.
Примерное содержание лекции.
При решении задач, связанных с вычислением длин отрезков (векторов) или величин углов удобнее рассматривать так называемые ортонормированные базисы.
Определение 2.1. Базис 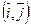 называется ортонормированным, если его векторы удовлетворяют двум условиям:
называется ортонормированным, если его векторы удовлетворяют двум условиям:  ;
;  .
.
 Теорема 2.2. Длина вектора
Теорема 2.2. Длина вектора  , заданного координатами в ортонормированном базисе
, заданного координатами в ортонормированном базисе 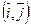 вычисляется по формуле
вычисляется по формуле

Доказательство.
1. Пусть  и
и  . Отложим векторы
. Отложим векторы  от некоторой точки О плоскости. Построим прямоугольник
от некоторой точки О плоскости. Построим прямоугольник  так, чтобы лучи
так, чтобы лучи  и
и  содержали бы векторы
содержали бы векторы  , а
, а  .
.
2. По теореме Пифагора имеем: 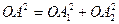 ,
, 
3. Так как 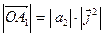 и
и  , то
, то  . Значит,
. Значит,  .
.
Пусть векторы  и
и  - ненулевые векторы. Отложим от произвольной точки О векторы
- ненулевые векторы. Отложим от произвольной точки О векторы  ,
,  и рассмотрим лучи
и рассмотрим лучи 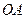 и
и  .
.
 Определение 2.3. Углом между векторами
Определение 2.3. Углом между векторами  и
и  называется угол между лучами их содержащими
называется угол между лучами их содержащими 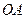 и
и  , если эти лучи не совпадают.
, если эти лучи не совпадают.
Если лучи 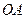 и
и  совпадают, то угол между ними считается равным нулю.
совпадают, то угол между ними считается равным нулю.
Угол между векторами  и
и  обозначается так:
обозначается так:  .
.
Так как два угла, стороны которых сонаправлены, равны, то угол между векторами не зависит от выбора точки О.
Определение 2.4. Скалярное произведение векторов равно произведению длин этих векторов на косинус угла между ними:  .
.
Из формулы заключаем, что  тогда и только тогда, когда векторы
тогда и только тогда, когда векторы 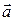 и
и  перпендикулярны. Это утверждение справедливо и в том случае, когда хотя бы один из векторов
перпендикулярны. Это утверждение справедливо и в том случае, когда хотя бы один из векторов 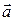 и
и  - нулевой. Скалярное произведение
- нулевой. Скалярное произведение  . Число
. Число  называется скалярным квадратом вектора
называется скалярным квадратом вектора 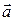 и обозначается через
и обозначается через 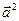 . Таким образом,
. Таким образом,  .
.
Теорема 2.5. Скалярное произведение двух векторов  и
и 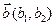 , заданных в ортонормированном базисе, есть число, равное сумме произведений соответствующих координат, т.е.
, заданных в ортонормированном базисе, есть число, равное сумме произведений соответствующих координат, т.е.  .
.
Доказательство.
 I. Пусть векторы
I. Пусть векторы  и
и 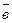 не нулевые и не коллинеарные.
не нулевые и не коллинеарные.
1. Рассмотрим треугольник  :
:
o по определению разности векторов имеем:  ;
;
o по теореме косинусов имеем: 
o Значит,  или
или 
o Так как  , то
, то  и
и  (*)
(*)
2. Распишем равенство (*) в координатах:

Таким образом, 
II. Пусть векторы 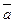 и
и  ненулевые и коллинеарные.
ненулевые и коллинеарные.
1. По теореме о коллинеарных векторах существует такое  , что
, что  , следовательно
, следовательно 
2. Найдем скалярное произведение векторов  и
и  по определению 3.4:
по определению 3.4: 
Следствие 2.6. Векторы  и
и  , заданные в ортонормированном базисе, взаимно перпендикулярны тогда и только, когда
, заданные в ортонормированном базисе, взаимно перпендикулярны тогда и только, когда  .
.
Следствие 2.7. Косинус угла между ненулевыми векторами  и
и  , заданными в ортонормированном базисе, вычисляется по формуле:
, заданными в ортонормированном базисе, вычисляется по формуле:

Свойства скалярного умножения 2.8.  Для любого действительного числа
Для любого действительного числа  и произвольных векторов
и произвольных векторов 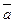 ,
,  и
и  справедливы следующие равенства:
справедливы следующие равенства:
2.8.1. 
2.8.2.  и
и 
2.8.3. 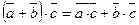
2.8.4. 
Ограничимся доказательством свойства 2.8.3. Остальные доказываются аналогично.
Доказательство свойства 2.8.3.
Так как вектор  имеет координаты
имеет координаты  , то по формуле скалярного произведения в ортонормированном базисе имеем:
, то по формуле скалярного произведения в ортонормированном базисе имеем:  =
=
 =
=  =
=  .
.
Геометрический смысл координат вектора.
1. Пусть в ортонормированном базисе задан некоторый вектор  . Его можно разложить по базису:
. Его можно разложить по базису: 
 2. Умножим обе части разложения вектора
2. Умножим обе части разложения вектора  скалярно на
скалярно на  ,
,  . Имеем:
. Имеем: 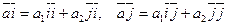 .
.
3. Учитывая, что  , имеем:
, имеем: 




Определение 2.5 Косинусы углов  между вектором
между вектором  и базисными векторами
и базисными векторами  ,
,  называются направляющими косинусами вектора
называются направляющими косинусами вектора  в ортонормированном базисе.
в ортонормированном базисе.
Если  , то
, то 
Задания по содержанию лекции
- Раскрыть вопросы лекции относительно двух векторов в пространстве, заполнив таблицу:
| Основные вопросы | Векторы на плоскости | Векторы в пространстве |
| Определение ортонормированного базиса: | ||
| Координаты вектора | ||
| Формула нахождения длины вектора в ортонормированном базисе | ||
| Определение скалярного произведения | ||
| Свойства скалярного произведения | ||
| Формула нахождения скалярного произведения в ортонормированном базисе | ||
| Определение угла между двумя векторами | ||
| Способы нахождения угла между двумя векторами |
- Доказать свойства скалярного произведения двух векторов (ортонормированный базис).
- Составить математическую карту изучения темы «Векторы на плоскости и в пространстве».
Замечание. Задания 1-2 выполняются студентами на лекционном занятии по группам.