Задание 9.1. Решить задачу:
В.1. В коллекции из 20 дисков имеется 5 дисков с песнями Трофима. Наугад выбирают 4 диска. Какова вероятность того, что 2 из них с произведениями Трофима?
В.2. На столе лежат 36 экзаменационных билетов с номерами 1, 2, 3,…,36. Преподаватель берет 3 любых билета. Какова вероятность того, что только один билет окажется из четырех первых номеров?
В.3. Из 15 мальчиков и 10 девочек составляется наудачу группа, в которой 5 человек. Какова вероятность того, что в неё попадут 3 мальчика и 2 девочки?
В.4. Из букв разрезной азбуки составлено слово «ремонт». Перемешаем карточки, затем, вытаскивая их наудачу, разложим в порядке вытаскивания. Какова вероятность того, что при этом получится слово «море»?
В.5. В ящике находятся 90 годных и 10 бракованных деталей. Найти вероятность того, что среди 10 вынутых из ящика деталей нет бракованных.
В.6. Контролер из партии 1000 деталей производит безвозвратную выборку 5 из них. Найти вероятность того, что в выборке не окажется дефектных деталей, если во всей партии их 4.
В.7. В урне 10 белых и 6 черных шаров. Из урны сразу вынимают 5 шаров. Найти вероятность того, что 2 из них будут белыми, а 3 черными.
В.8. В лотерее 100 билетов, из них 40 выигрышных. Какова вероятность того, что ровно один из трех взятых билетов окажется выигрышным?
В.9. Бросают две игральные кости. Какова вероятность того, что сумма выпавших очков: а) кратна 3; б) равна 7, а разность равна 3; в) равна 7, если известно, что разность их равна 3; г) не менее 7, если известно, что разность их равна 3.
В.10. На пяти карточках написано по одной цифре из набора 1, 2, 3, 4, 5. Наугад выбирают одну за другой две карточки. Какова вероятность того. Что число на первой карточке будет больше, чем на второй?
|
|
Задание 9.2. Решить задачу:
В.1. Вероятность того, что студент сдаст первый экзамен, равна 0,9, второй – 0,9, третий – 0,8. Вычислить вероятность того, что хотя бы два экзамена будут сданы.
В.2. Три спортсмена участвуют в отборочных соревнованиях. Вероятности зачисления в сборную команду первого, второго и третьего спортсменов соответственно равны 0,8; 0,7; 0,6. Найти вероятность того, что хотя бы один из этих спортсменов попадет в сборную.
В.3. На каждые 100 электрических ламп завода «А» в среднем приходится 83 стандартных, завода «В» - 63 стандартных. В магазин поступает 70% лампочек с завода «А» и 30% - с завода «В». Купленная лампочка оказалась стандартной. Определить вероятность того, что лампочка изготовлена на заводе «А».
В.4. На сборку попадают детали с трех автоматов. Известно, что первый автомат дает 0,3% брака, второй – 0,2%, третий –0,4%. Найти вероятность попадания на сборку бракованной детали, если с первого автомата поступило 1000 деталей, со второго – 2000, а с третьего – 2500.
В.5. Вероятность попадания в цель для первого стрелка равна 0,8, для второго – 0,7, для третьего-0,9. Каждый из стрелков делает по одному выстрелу. Какова вероятность того, что в мишени 3 пробоины?
В.6. На склад поступили электрические лампы трех партий. Известно, что в первой партии, состоящей из 400 штук, содержится 1% нестандартных, во второй, состоящей из 500 штук - 2%, в третьей, состоящей из 100 штук - 4% нестандартных деталей. Со склада лампы поступили в магазин и здесь оказались расположенными случайным образом. Определить вероятность того, что покупатель, взявший одну лампу, купит нестандартную. В.7. Партия состоит из вентиляторов рижского и московского заводов. В партии 70% вентиляторов рижского завода. Для вентилятора московского завода вероятность безотказной работы в течение времени t равна 0,95, рижского – 0,92. Прибор испытывался в течение времени t и работал безотказно. Найти вероятность того, что это вентилятор московского завода.
|
|
В.8. Имеется две колоды по 36 карт. Из каждой колоды наудачу выбрали по карте. Найти вероятность того, что это были два туза.
В.9. Телевизор может принадлежать к одной из трех партий с вероятностями 0,25; 0,5; 0,25. Вероятности того, что телевизор проработает больше 10 лет, равны для этих партий соответственно 0,1; 0,2; 0,4. Определить вероятность того, что телевизор проработает больше 10 лет.
В.10. Вероятность поражения мишени при одном выстреле первым стрелком равна 0,8, вторым – 0,9. Найти вероятность того, что мишень будет поражена хотя бы стрелком.
Задание 9.3. Решить задачи:
В.1. Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредится, равна 0,0002. Найти вероятность того, что на базу поступит ровно три негодных изделия.
В.2. При массовом производстве полупроводниковых диодов вероятность брака при формовке равна 0,1. Какова вероятность того, что из 400 наугад взятых диодов 50 будет бракованных?
В.3. Всхожесть партии ржи равна 90%. Чему равна вероятность того, что из семи посеянных семян взойдут пять?
В.4. Игральная кость подброшена 10 раз. Найти вероятность выпадения единицы 7 раз.
В. 5. Стрелок сделал 30 выстрелов с вероятностью попадания при отдельном выстреле 0,3. Найти вероятность того, что при этом будет 8 попаданий.
|
|
В.6. В магазин вошли 8 покупателей. Найти вероятность того, что трое из них совершат покупки, если для каждого вошедшего вероятность совершить покупку равна 0,3.
В.7. В магазин вошли 12 покупателей. Найти вероятность того, что 4 из них сделают покупку, если вероятность совершить покупку для каждого одна и та же и равна 0,2.
В.8. Вероятность брака при изготовлении часов равна 0,0002. С конвейера сошло 5000 часов. Найти вероятность того, что среди всех часов, сошедших с конвейера, не более трёх бракованных.
В.9. Вероятность поражения мишени стрелком при одном выстреле равна 0,75. Найти вероятность того, что при 100 выстрелах стрелок поразит мишень: а) не менее 71 и не более 80 раз; б) ровно 75 раз.
В.10. На некотором предприятии произведено 400 изделий в смену. Вероятность того, что изделие будет первого сорта, равна 0,75. Какова вероятность того, что 280 изделий будет первого сорта?
Задание 9.4. Решить задачи:
В.1. Найти математическое ожидание M(X), дисперсию D(X), среднее квадратическое отклонение σ(Х), функцию распределения дискретной случайной величины Х:
| Х | 1,4 | 1,8 | 2,3 | 3,2 |
| Р | 0,3 | 0,4 | 0,2 | 0,1 |
В.2. Написать закон распределения вероятностей и функцию распределения числа попаданий мячом в корзину при двух бросках, если вероятность попаданий р =0,4.
В.3. У нормально распределенной случайной величины Х известны M(X) = 10 и D(X) = 4. Найти вероятность Р (12 < Х < 14).
В.4. Найти M(X), D(X), σ(Х), функцию распределения случайной величины Х, если она задана законом распределения:
| Х | |||||
| Р | 0,1 | 0,1 | 0,3 | 0,4 | 0,1 |
В.5. Найти M(X), D(X), σ(Х), функцию распределения дискретной случайной величины Х, если она задана законом распределения:
| Х | ||||
| Р | 0,2 | 0,5 | 0,2 | 0,1 |
В.6. Найти вероятность того, что нормальная случайная величина с M(X) = 1, D(X) = 4 примет значение из интервала (0, 2).
В.7. Случайная величина Х задана функцией распределения:
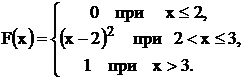
Вычислить вероятность попадания случайной величины Х в интервалы (1; 2,5) и (2,5; 3,5).
В.8. Случайная величина Х имеет функцию плотности
По какому закону распределена случайная величина? Найти M(X), D(X), σ(Х) и её функцию распределения.
В.9. Функция плотности некоторой случайной величины имеет вид
Найти M(X); D(X); σ(Х); F(x).
В.10. Случайная величина задана функцией распределения
Найти вероятность того, что в результате испытания Х примет значение, заключенное в интервале (0; 2). Найти f (х). Построить графики f (х); F (x).
Задание 9.5.
Вариант 1. Для нахождения средней цены продовольственной корзины из 1000 городов России было отобрано случайным образом 100 городов. Полученные данные представлены в таблице:
| Стоимость продовольственной корзины, тыс. руб | 0 – 2 | 2 – 4 | 4 – 6 | 6 – 8 | 8 – 10 | Итого |
| Число городов |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя 
- критерий Пирсона, на уровне значимости 
= 0,05 проверить гипотезу о том, что случайная величина X – стоимость продовольственной корзины – распределена по нормальному закону.
Вариант 2. Данные о продолжительности телефонных переговоров, отобранные по схеме собственно-случайной бесповторной выборки, приведены в таблице:
| Время, мин | Менее 1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | 7-8 | Более | Итого |
| Число разговоров |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – продолжительность телефонных разговоров – распределена по нормальному закону.
Вариант 3. В результате выборочного обследования российских автомобилей, обслуживаемых в автосервисе по гарантии, по схеме собственно-случайной бесповторной выборки были проверены 100 автомобилей. Полученные данные о пробеге автомобилей с момента покупки до первого гарантийного ремонта приведены в таблице:
| Пробег, тыс. км | Менее 1 | 1-2 | 2-3 | 3-4 | 4-5 | 5-6 | 6-7 | Более 7 | Итого |
| Число автомобилей |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – пробег автомобиля с момента покупки до первого гарантийного ремонта – распределена по нормальному закону.
Вариант 4. Для изучения стажа работы студентов по специальности было отобрано 100 студентов. Полученные данные о стаже работы студентов по специальности представлены в таблице:
| Стаж работы по специальности, лет | Менее 2 | 2-4 | 4-6 | 6-8 | 8-10 | 10-12- | Более | Итого |
| Количество студентов |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – стаж работы студента по специальности – распределена по нормальному закону.
Вариант 5. Для изучения средней продолжительности обслуживания клиентов в Пенсионном фонде было проведено обследование 100 клиентов. Результаты обследования представлены в таблице:
| Время обслуживания, мин | Менее 4 | 4-8 | 8-12 | 12-16 | 16-20 | 20-24- | Более | Итого |
| Количество клиентов |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – стаж работы студента по специальности – распределена по нормальному закону.
Вариант 6. Для получения статистических данных о пребывании на больничном листе в течение года было отобрано 100 работников предприятия. Полученные данные представлены в таблице:
| Количество дней пребывания на больничном листе | Менее 3 | 3-5 | 5-7 | 7-9 | 9-11 | 11-13 | Более | Итого |
| Количество работников |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – количество дней пребывания работника предприятия на больничном листе – распределена по нормальному закону.
Вариант 7. Имеются выборочные данные о распределении вкладчиков по размеру вклада в Сбербанке города:
| Размер вклада, тыс.руб | До 50 | 50-100 | 100-150 | 150-200 | 200-250 | Более | Итого |
| Количество вкладчиков |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – размер вклада в Сбербанке города – распределена по нормальному закону.
Вариант 8. По схеме собственно-случайной бесповторной выборки было проведено обследование 50 строительных организаций региона по объему выполненных работ. Результаты представлены в таблице:
| Объем работ, млн.руб | До 30 | 30-60 | 60-90 | 90-120 | 120-150 | 150-180 | Более 180 | Итого |
| Количество организаций |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – объем выполненных работ – распределена по нормальному закону.
Вариант 9. В результате выборочного обследования стажа работы профессорско-преподавательского состава вуза получены следующие данные:
| Стаж работы (лет) | 0-4 | 4-8 | 8-12 | 12-16 | 16-20 | 20-24 | 24-28 | 28-32 |
| Число преподавателей |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – стаж работы студента по специальности – распределена по нормальному закону.
Вариант 10.
Во время медосбора были получены следующие выборочные данные о суточной прибавке меда на пасеках области:
| Суточная прибавка (кг) | 0-2 | 2-4 | 4-6 | 6-8 | 8-10 | Более 10 | Итого |
| Количество пчелосемей |
1. Постройте полигон и гистограмму относительных частот (частностей);
2. Найдите выборочную среднюю, дисперсию, «исправленную» выборочную дисперсию;
3. Найдите доверительный интервал для оценки с надежностью 0,95 неизвестного математического ожидания а нормально распределенного признака X генеральной средней.
4. Используя - критерий Пирсона, на уровне значимости = 0,05 проверить гипотезу о том, что случайная величина X – суточная прибавка меда на пасеках области – распределена по нормальному закону.