| Рис. 2.11. Распределение относительных главных напряжений в сечении x = 0 цилиндрического стержня из идеального упругого («е » – штриховые линии) и идеального упругопластического («р » – сплошные линии) материала, а также зона пластического деформирования по допуску 0,1% (расчет МКЭ А.С. Хоружего) |
Рис. 2.11 иллюстрирует распределение главных напряжений в цилиндрическом стержне с глубокой гиперболической выточкой, отнесенных к номинальному напряжению в нетто–сечении, превышающему предел текучести материала. Для сравнения там же приведены графики относительных главных напряжений в предположении упругой работы материала.
Анализ напряженно-деформированного состояния цилиндра как в упругой, так и неупругой (с использованием критерия текучести Мизеса) постановке был выполнен методом конечных элементов. Корректность построенной конечно-элементной модели подтверждена соответствием известному аналитическому «упругому» решению.
| Рис. 2.14. Сопоставление результатов расчета деформации в опасной точке у мелкого гиперболического надреза с помощью приближенных зависимостей и численным методом с экспериментальными данными (по С.А. Куркину) |
не имеет общего теоретического обоснования (автор основывался на расчетах, выполненных для конкретной задачи). Однако эксперименты, проведенные различными исследователями, а также расчеты на основе моделей упругопластического деформирования, позволяющие определить поля напряжений и деформаций вблизи концентратора, показали неплохое ее соответствие. На рис. 2.14 показано сопоставление результатов расчета деформации в опасной точке пластины с двусторонним мелким надрезом остротой t /r = 2,02 (k Т 2 = 3,8) по формулам Хардрата–Омана (2.18), Нейбера (2.19) и методом конечных элементов с данными опытов.
Анализируя результаты, приведенные на рис. 2.14, отметим, что наилучшее совпадение с опытными данными показал расчет методом конечных элементов; отклонение при больших s nom связано с изменением радиуса надреза вследствие пластического деформирования материала, что не учитывалось в расчете.
Подход Нейбера обеспечивает вполне удовлетворительное соответствие эксперименту, если номинальное напряжение не превосходит предела текучести. Этот вывод согласуется с данными Н.А. Махутова, установившим, что для материалов с незначительным упрочнением в упругопластической области и для объектов с высокой концентрацией напряжений формула Нейбера предсказывает завышенные значения местных деформаций и напряжений. В научно-технической литературе имеются предложения по уточнению формулы Нейбера путем включения в нее коэффициента, отражающего тип концентратора (его «остроту»).
Прогноз по формуле Хардрата–Омана при s nom ³ 0,5 s 0,2 оказывается, как видно, неприемлемо консервативен.
| Рис. 2.15. Влияние остроты концентратора и режима термомеханической обработки (1 – отжиг; 2 – предварительная пластическая деформация e р 0 = 10 %; 3 – – предварительная пластическая деформация e р 0 = 10 %, старение при Т = 250° С)
|
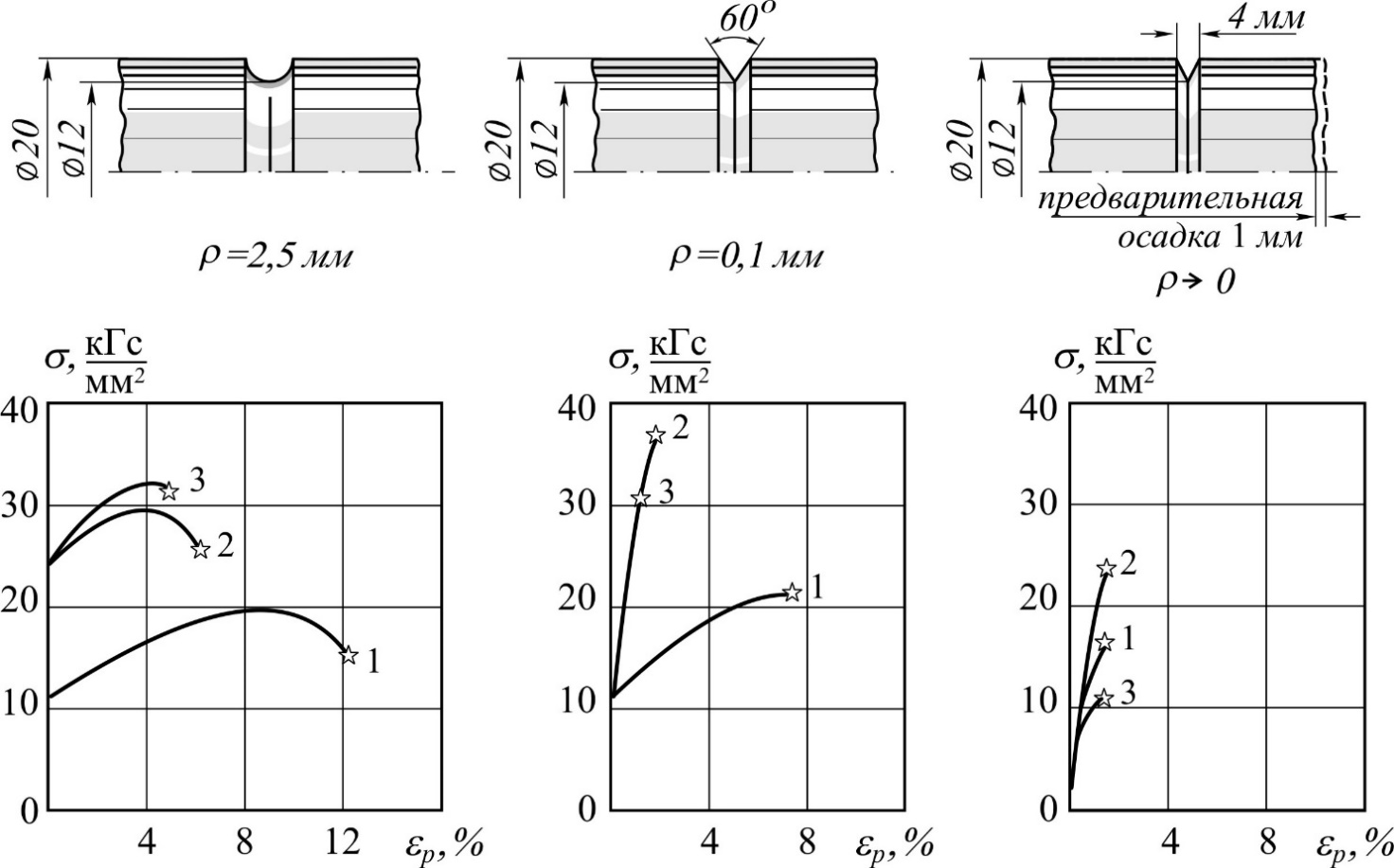Из рис. 2.15 следует, что для концентраторов различной остроты влияние термообработки, предварительного пластического деформирования, деформационного старения не вполне идентично. Так предварительная пластическая деформация и старение уменьшают отношение s В / s 0,2и снижают ресурс пластичности материала.
Контрольные вопросы и упражнения