Электрическое поле
Закон Кулона, был установлен экспериментально и справедлив для покоящихся заряженных тел. Каким же образом происходит взаимодействие заряженных тел на расстоянии? До некоторых пор при изучении электрических взаимодействий бок о бок развивались две принципиально разные теории: теория близкодействия и теория дальнодействия (действия на расстоянии).
Теория близкодействия заключается в том, что заряженные тела взаимодействуют друг с другом посредством промежуточного звена (например, цепь в задаче о поднятии ведра из колодца является промежуточным звеном, посредством которого мы воздействуем на ведро, то есть поднимаем его).
Теория дальнодействия гласит, что заряженные тела взаимодействуют через пустоту. Шарль Кулон придерживался именно этой теории и говорил, что заряженные тела «чувствуют» друг друга. В начале XIX века конец спорам положил Майкл Фарадей (рис. 1). В работах, связанных с электрическим полем, он установил, что между заряженными телами существует некий объект, который и осуществляет действие заряженных тел друг на друга. Работы Майкла Фарадея были подтверждены Джеймсом Максвеллом (рис. 2). Он показал, что действие одного заряженного тела на другое распространяется за конечное время, таким образом, между заряженными телами должно существовать промежуточное звено, через которое осуществляется взаимодействие.

Рис. 1. Майкл Фарадей (Источник)

Рис. 2. Джеймс Клерк Максвелл (Источник)
Электрическое поле – это особая форма материи, которая создается покоящимися зарядами и определяется действием на другие заряды.
Напряженность
Электрическое поле характеризуется определенными величинами. Одна из них называется напряженностью.
Вспомним, что по закону Кулона, сила взаимодействия двух зарядов:
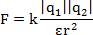
Максвелл показал, что это взаимодействие осуществляется за конечное время:

где l – расстояние между заряженными частицами, а c – скорость света, скорость распространения электромагнитных волн.
Рассмотрим эксперимент по взаимодействию двух зарядов. Пусть электрическое поле создается положительным зарядом +q 0, и в это поле на некотором расстоянии помещается пробный, точечный положительный заряд +q (рис. 3,а). Согласно закону Кулона, на пробный заряд будет действовать сила электростатического взаимодействия со стороны заряда, создающего электрическое поле. Тогда отношение этой силы к величине пробного заряда будет характеризовать действие электрического поля в данной точке. Если же в эту точку будет помещен вдвое больший пробный заряд, то сила взаимодействия также увеличится вдвое (рис. 3,б). Аналогичным образом отношение силы к величине пробного заряда снова даст значение действия электрического поля в данной точке. Так же действие электрического поля определяется и в том случае, если пробный заряд отрицательный (рис. 3,в).

Рис. 3. Сила электростатического взаимодействия двух точечных зарядов
Таким образом, в точке, где находится пробный заряд, поле характеризуется величиной:
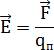
Эта величина и называется напряженностью электрического поля. Напряженность поля в данной точке не зависит от величины пробного заряда: во всех трех случаях отношение силы к величине заряда – постоянная величина. Единица измерения напряженности:
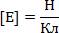
Напряженность – векторная величина, является силовой характеристикой электрического поля, направлена в ту же сторону, куда и сила электростатического взаимодействия. Она показывает, с какой силой электрическое поле действует на помещенный в него заряд.
Напряженность поля точечного заряда
Рассмотрим напряженность электрического поля уединенного точечного заряда либо заряженной сферы.
Из определения напряженности следует, что для случая взаимодействия двух точечных зарядов, зная силу их кулоновского взаимодействия, можем получить величину напряженности электрического поля, которое создается зарядом q 0 в точке на расстоянии r от него до точки, в которой исследуется электрическое поле:
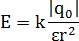
Данная формула показывает, что напряженность поля точечного заряда изменяется обратно пропорционально квадрату расстояния от данного заряда, то есть, например, при увеличении расстояния в два раза, напряженность уменьшается в четыре раза.
Линии напряженности
Попытаемся теперь охарактеризовать электростатическое поле нескольких зарядов. В этом случае необходимо воспользоваться сложением векторных величин напряженностей всех зарядов. Внесем пробный заряд и запишем сумму векторов сил, действующих на этот заряд. Результирующее значение напряженности получится при разделении значений этих сил на величину пробного заряда. Данный метод называется принципом суперпозиции.
Напряженность электростатического поля принято изображать графически при помощи силовых линий, которые также называют линиями напряженности. Такое изображение можно получить, построив вектора напряженности поля в как можно большем количестве точек вблизи данного заряда или целой системы заряженных тел.
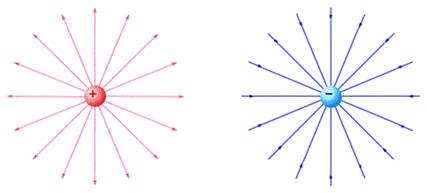
а) положительного б) отрицательного
Рис. 4. Линии напряженности электрического поля точечного заряда.
Рассмотрим несколько примеров изображения силовых линий. Линии напряженности выходят из положительного заряда (рис. 4,а), то есть положительный заряд является источником силовых линий. Заканчиваются линии напряженности на отрицательном заряде (рис. 4,б).
Рассмотрим теперь систему, состоящую из положительного и отрицательного зарядов, находящихся на конечном расстоянии друг от друга (рис. 5). В этом случае линии напряженности направлены от положительного заряда к отрицательному.
Большой интерес представляет электрическое поле между двумя бесконечными плоскостями. Если одна из пластин заряжена положительно, а другая отрицательно, то в зазоре между плоскостями создается однородное электростатическое поле, линии напряженности которого оказываются параллельными друг другу (рис. 6).

Рис. 5. Линии напряженности системы двух зарядов

Рис. 6. Линии напряженности поля между заряженными.
В случае неоднородного электрического поля величина напряженности определяется густотой силовых линий: там, где силовые линии гуще, величина напряженности поля больше (рис. 7).

Рис. 7. Неоднородное электрическое поле
Линиями напряженности называют непрерывные линии, касательные к которым в каждой точке совпадают с векторами напряженности в этой точке.
Линии напряженности начинаются на положительных зарядах, заканчиваются на отрицательных и являются непрерывными.
Изображать электрическое поле с помощью силовых линий мы можем так, как сами посчитаем нужным, то есть число силовых линий, их густота ничем не ограничивается. Но при этом необходимо учитывать направление векторов напряженности поля и их абсолютные величины.
Очень важно следующее замечание. Как говорилось ранее, закон Кулона применим только для точечных покоящихся зарядов, а также заряженных шариков, сфер. Напряженность же позволяет характеризовать электрическое поле вне зависимости от формы заряженного тела, которое это поле создает.
5. Работа электрического поля
Темой сегодняшнего урока будет ещё одна характеристика электрического поля – энергетическая. Эта характеристика называется потенциалом, и она непосредственно связана с работой электрического поля по перемещению заряда. Но для начала вспомним другую характеристику поля – силовую характеристику, напряженность:
для произвольного поля в некоторой точке пространства напряженность равна:

а для поля точечного заряда:
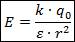
Теперь вспомним из курса механики, как вычислить работу, совершаемую над телом – в нашем случае электрическое поле совершает работу по перемещению заряда:
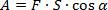
учитывая:
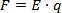
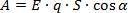
Для простоты рассмотрим случай однородного электрического поля, которое можно получить между двумя заряженными пластинами. И пусть положительный заряд изначально находится вблизи положительной пластинки, тогда, естественно, он начнёт под действием кулоновских сил движение в сторону отрицательной пластинки (см. рис. 1).

Рис. 1
Для этого случая из-за параллельности векторов силы и перемещения выражение для работы принимает следующий вид:
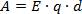
где d- расстояние между пластинами.
Более того, даже для любого произвольного движения заряда от пластины «+» к пластине «-» будет определяться по такой же формуле (см рис. 2).

Рис. 2
Любую прямую или кривую можно представить в виде большого числа маленьких «ступенек». А, как известно, если сила перпендикулярна перемещению, работа на таких участках равна нулю, так как. То есть сумма работ на «ступеньках» равна сумме работ на их горизонтальных частях, то есть исходному значению.
Также нам известно, что потенциальная энергия заряда уменьшается по мере прохождения, поэтому работа электрического поля имеет вид: 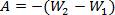
Потенциал
Теперь пришло время ввести новую энергетическую характеристику поля – потенциал.
Потенциал – физическая величина, показывающая отношение потенциальной энергии заряда в некоторой точке пространства к величине этого заряда:

Так как потенциальная энергия заряда прямо пропорциональна величине заряда, то потенциал от величины заряда не зависит:

Единица измерения потенциала – вольт (В):
Потенциал некоторой точки пространства можно определить как работу электрического поля по переносу единичного заряда из бесконечности в эту точку. В общем же виде связь потенциала с работой можно задать через ввод электрического напряжения:

Полученная зависимость справедлива вдоль некоторой силовой линии, и здесь – расстояние между двумя точками на одной силовой линии.
Зависимость потенциала поля точечного заряда от расстояния имеет похожий вид с аналогичной зависимостью для напряженности, однако убывает медленнее – не пропорционально квадрату, а пропорционально первой степени:
