Глава 6. Кривые второго порядка
| Уравнение | Чертеж | Фокусы | Эксцентриситет | Директриса | Асимптота |
1. Эллипс

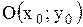 - центр - центр
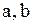 - полуоси - полуоси
| 
| Если 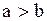 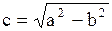
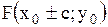
| 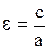
| 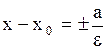
| – |
Если  
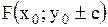
| 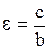
| 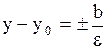
| – | ||
2. Гипербола

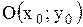 - центр - центр
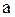 - действительная полуось, - действительная полуось,
 - мнимая - мнимая
| 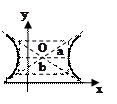
| 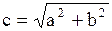
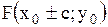
| 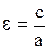
| 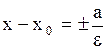
| 
|
3. Гипербола
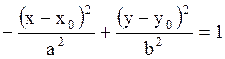 или
или
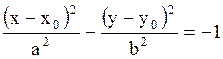
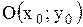 - центр - центр
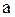 - мнимая полуось, - мнимая полуось,
 - действительная - действительная
| 
| 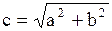
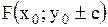
| 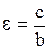
| 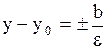
| 
|
4. Парабола
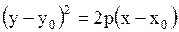
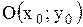 - вершина - вершина
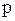 - расстояние между фокусом и директрисой - расстояние между фокусом и директрисой
| 
| 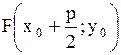
| - | 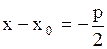
| - |
5. Парабола

| 
| 
| - | 
| - |
6. Парабола

| 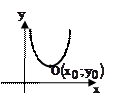
| 
| - | 
| - |
7. Парабола

| 
| 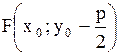
| - | 
| - |
8. Окружность

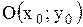 - центр - центр
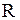 - радиус - радиус
| 
| - | 
| - | - |
9. Две пересекающиеся прямые
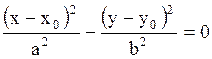
| 
| - | - | - | - |
10. Уравнение
 определяет точку определяет точку 
| - | - | - | - | - |
Задача.
Укажите соответствие между кривыми второго порядка и их уравнениями:
1. 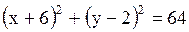 2. 2.  3. 3.  4. 4. 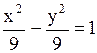 Варианты ответов: А) эллипс В) гипербола С) окружность D) парабола
Решение.
Проанализируем каждое уравнение
1). Уравнение можно записать в виде
Варианты ответов: А) эллипс В) гипербола С) окружность D) парабола
Решение.
Проанализируем каждое уравнение
1). Уравнение можно записать в виде  . Это уравнение окружности.
2). Уравнение содержит переменную . Это уравнение окружности.
2). Уравнение содержит переменную  во второй степени, а переменную во второй степени, а переменную 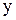 - в первой. Это уравнение параболы.
3). Поделим уравнение на 4. Тогда - в первой. Это уравнение параболы.
3). Поделим уравнение на 4. Тогда  . Обе переменные в квадрате. В левой части – сумма; в правой – единица. Это уравнение эллипса.
4). . Обе переменные в квадрате. В левой части – сумма; в правой – единица. Это уравнение эллипса.
4). 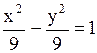 . Обе переменные во второй степени. В левой части – разность; в правой – единица. Это уравнение гиперболы.
Ответ: . Обе переменные во второй степени. В левой части – разность; в правой – единица. Это уравнение гиперболы.
Ответ:   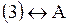  Задача.
Установите соответствие между кривой второго порядка и ее уравнением.
1. Парабола 2. Эллипс 3. Гипербола
Варианты ответов: А)
Задача.
Установите соответствие между кривой второго порядка и ее уравнением.
1. Парабола 2. Эллипс 3. Гипербола
Варианты ответов: А)  В) В)  С) С) 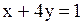 D) D) 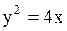 Е) Е)  Решение.
1). Парабола. В уравнении одна переменная должна быть в первой степени, другая – во второй. Это уравнение (D).
2). Эллипс. Обе переменные должны быть во второй степени. В левой части – сумма; в правой – единица. Это уравнение (Е).
3). Гипербола. Обе переменные должны быть во второй степени. В левой части – разность; в правой – единица. Это уравнение (В)
Ответ:
Решение.
1). Парабола. В уравнении одна переменная должна быть в первой степени, другая – во второй. Это уравнение (D).
2). Эллипс. Обе переменные должны быть во второй степени. В левой части – сумма; в правой – единица. Это уравнение (Е).
3). Гипербола. Обе переменные должны быть во второй степени. В левой части – разность; в правой – единица. Это уравнение (В)
Ответ:   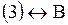 Задача.
Если
Задача.
Если  - центр окружности, которая проходит через точку - центр окружности, которая проходит через точку 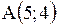 , то уравнение этой окружности имеет вид…
Варианты ответов: 1) , то уравнение этой окружности имеет вид…
Варианты ответов: 1) 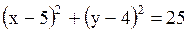 2) 2)  3)
3)  4) 4)  Решение.
Так как
Решение.
Так как  - центр, то уравнение может быть №3 или №4. Найдем радиус – это расстояние АС. - центр, то уравнение может быть №3 или №4. Найдем радиус – это расстояние АС.
 . Итак, . Итак, 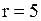 , тогда уравнение №3.
Ответ: №3.
Задача. , тогда уравнение №3.
Ответ: №3.
Задача.
 Если уравнение гиперболы имеет вид Если уравнение гиперболы имеет вид 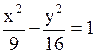 , то длина ее действительной полуоси равна…
Варианты ответов: 1) 3 2) 16 3) 9 4) 4
Решение.
Действительная полуось берется из положительного слагаемого , то длина ее действительной полуоси равна…
Варианты ответов: 1) 3 2) 16 3) 9 4) 4
Решение.
Действительная полуось берется из положительного слагаемого  . Тогда . Тогда 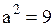 , , 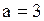 .
Ответ: №1.
Задача.
Если уравнение окружности имеет вид .
Ответ: №1.
Задача.
Если уравнение окружности имеет вид  , то его центром С и радиусом r являются…
Варианты ответов: 1) , то его центром С и радиусом r являются…
Варианты ответов: 1)  , ,  2) 2)  , ,  3) 3)  , ,  4) 4)  , ,  Решение.
Уравнение можно записать в виде
Решение.
Уравнение можно записать в виде 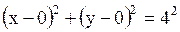 . Тогда центр . Тогда центр  , радиус , радиус  .
Ответ: №2.
Задача.
Радиус окружности, заданной уравнением .
Ответ: №2.
Задача.
Радиус окружности, заданной уравнением 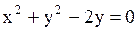 , равен …
Варианты ответов: 1) 3 2) -1 3) 4 4) 1
Решение. , равен …
Варианты ответов: 1) 3 2) -1 3) 4 4) 1
Решение.
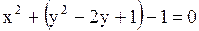 ; ; 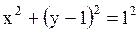 . Тогда центр . Тогда центр  , радиус , радиус 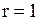 .
Ответ: №4. .
Ответ: №4.
|
Глава 7. Поверхности второго порядка
| Уравнение | Чертеж | Задачи |
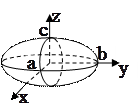
1. Эллипсоид
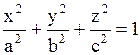
| 
| Задача.
Установите соответствие между изображением поверхности и ее каноническим уравнением.
1. 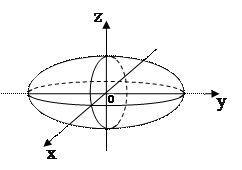 2.
2.  3. 3.  Варианты ответов: А)
Варианты ответов: А)  В)
В) 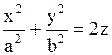 С) С)  D) D) 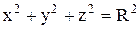 Решение.
Сравнивая уравнение и изображение, определяем соответствие
Ответ:
Решение.
Сравнивая уравнение и изображение, определяем соответствие
Ответ: 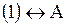  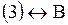
|
2. Однополостный гиперболоид
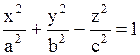
| 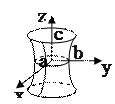
| |
3. Двуполостный гиперболоид
 или или
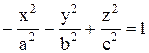
| 
| |
4. Эллиптический параболоид

| 
| |
5. Цилиндр
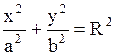
| 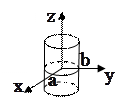
| |
6. Сфера
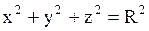
| 
|
Глава 8. Дифференциальная геометрия
| §1 Уравнение касательной и нормали к кривой | ||||
Для кривой  в точке в точке 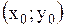
| Для кривой  в точке в точке 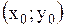
| Для кривой 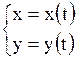
| Для кривой 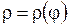
| |
| 1. Уравнение касательной | 
| 
| 
| - |
| 2. Уравнение нормали | 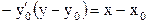
| 
| 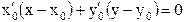
| - |
| §2 Кривизна кривой | ||
3. Кривизна для кривой 
| 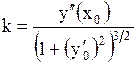
| Задача.
Кривизна линии  в точке в точке 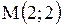 равна…
Варианты ответов: 1) равна…
Варианты ответов: 1) 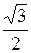 2) 2)  3) 3)  4) 4) 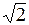 Решение.
Воспользуемся предложенной формулой
Решение.
Воспользуемся предложенной формулой  ; ;  ; ;  .
Подставим в полученные производные координаты точки .
Подставим в полученные производные координаты точки  , тогда , тогда 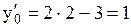 , , 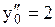
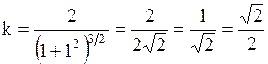 Ответ: №3.
Ответ: №3.
|
4. Кривизна для кривой 
| 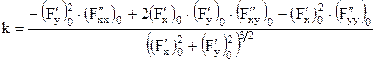
| |
5. Кривизна для кривой 
| 
| |
6. Кривизна для кривой 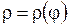
| 
| |
| 7. Радиус кривизны | Радиус кривизны вычисляется по формуле 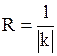 , где k – кривизна , где k – кривизна
| Представление о знаке кривизны дает рисунок

|
| §3 Поверхность | |||
| 8. Уравнение касательной плоскости | Уравнение касательной плоскости к поверхности  в точке в точке 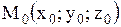
|

| Задача.
Уравнение касательной плоскости к поверхности 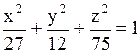 в точке в точке  имеет вид…
Варианты ответов:
1) имеет вид…
Варианты ответов:
1)  2) 2) 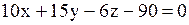 3)
3) 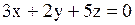 4) 4)  Решение.
Решение.
 Найдем частные производные
Найдем частные производные
 ; ; 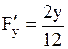 ; ; 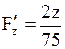 Подставим координаты точки
Подставим координаты точки 
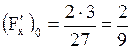 ; ;  ; ; 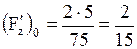 Уравнение касательной плоскости примет вид
Уравнение касательной плоскости примет вид
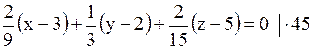 

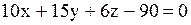 Ответ: №2.
Ответ: №2.
|
Уравнение касательной плоскостик поверхности 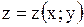 в точке в точке 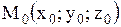
|
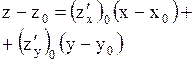
| ||
| 9. Уравнение нормали | Уравнение нормалиплоскости к поверхности  в точке в точке 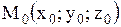
| 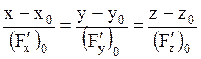
| |
Уравнение нормали к поверхности 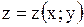 в точке в точке 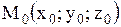
| 
|