Для создания потока и отбрасывания массы рабочего тела с заданной скоростью реактивный двигатель реализуется как тепловая машина, преобразующая химическую энергию топлива в кинетическую энергию газовой струи.
Реактивная сила появляется вследствие истечения газов из летательного аппарата, приложена к нему и направлена противоположно скорости истечения газов относительно летательного аппарата.
Рабочее тело
| Тепловой двигатель |
Реактивная сила Истечение газов
Энергия
Рис. 1. Принцип реактивного движения
Принцип действия реактивных сил основан на законе сохранения количества движения:
. (*)
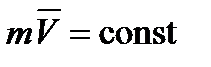Количество движения системыопределяют из выражения:
,
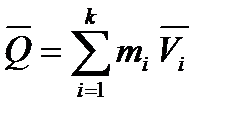где mi, Vi – масса и скорость движения i- ой точки системы, соответственно.
Произведение силы на время называют импульсом силы.
Закон сохранения количества движения представляют теоремой:
Изменение количества движения системы материальных точек равно сумме импульсов внешних сил, действующих на эту систему:
.
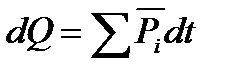Или после преобразования можно записать математическое выражение приведенной теоремы:
,
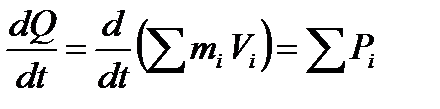где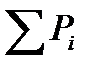 
– сумма всех внешних сил, действующих на материальные точки тi рассматриваемой системы.
Необходимо отметить, что в системе внутренние силы всегда взаимно уравновешены, т.е.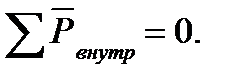 
Из формулы второго закона Ньютона Р = т∙а (произведение массы тела на ускорение его движения) можно записать
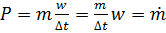w.
Из этого следует, что реактивная сила определяется скоростью истечения газов и расходом топлива, и будет создаваться только тогда, когда есть истечение газа из сопла. Величина ее зависит от массы и скорости вытекающих из сопла газов. Таким образом, реактивный двигатель создает движущую летательный аппарат силу непосредственно, без помощи каких-либо промежуточных элементов.
Рассмотрим далее движение тела переменной массы М со скоростью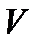 
(рис. 2). Примером может выступать полет ракеты, масса которой непрерывно убывает вследствие расхода топлива.
| М |
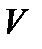
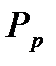
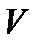
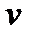
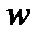
m
Рис. 2. Движение тела переменной массы
Пусть за элементарный отрезок времени ∆t в результате действия внутренних сил от тела массой М отделилась элементарная масса m с относительной к этому телу скоростью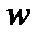 
.
Для элементарной массы m имеем
переносную – V,
относительную – w
и абсолютную скорость – (v = V – w).
Количество движения системы (тела М)до отделения элементарной массы равно (*)
Q 0 = М V.
Количество движения системы, состоящей из двух тел: (М – m) и m, после отделения элементарной массы составит
Q 1 = (М – m)(V + ∆ VМ ) + mv
или
Q 1 = (М – m)(V + ∆ VМ ) + m (V – w),
где ∆ VМ –значения изменений абсолютных скоростей за время dt для тела массы (М – т) и v – для тела т.
Изменение количества движения системы при отсутствии воздействия внешних сил будет равно разности значений до и после отделения элементарной массы:
∆ Q = Q 1 – Q 0 = (M – m)(V +∆ VМ) + m (V – w) – М V = 0 .
Тогда, преобразуя полученное выражение, можно записать
(M – m) ∆ VМ = m w.
Тогда импульс силы Р Δ t, действующий на массу (М – т) и вызывающий изменение ее скорости на величину ∆ VМ за время ∆ t, равен
,
и сила Р – реактивная сила – находится из выражения:
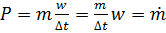w.
