Допустим, что адиабатически изолированная система находится в термодинамическом равновесии, причем ее энтропия S в рассматриваемом состоянии максимальна, т. е. больше энтропий всех возможных бесконечно близких состояний, в которые система может перейти без подвода или отвода тепла. Тогда можно утверждать, что самопроизвольный адиабатический переход системы во все эти состояния невозможен, т. е. система находится в устойчивом термодинамическом равновесии. Действительно, если бы такой переход был возможен, то энтропии начального 1 и конечного 2 состояний были бы связаны соотношением 
. Но это соотношение находится в противоречии с принципом возрастания энтропии, согласно которому при адиабатических переходах должно быть 
. Таким образом, мы приходим к следующему критерию термодинамической устойчивости.
Если система адиабатически изолирована и ее энтропия в некотором равновесном состоянии максимальна, то это состояние являемся термодинамически устойчивым. Это значит, что система, оставаясь адиабатически изолированной, не может самопроизвольно перейти ни в какое другое состояние.
В приложениях термодинамики к конкретным вопросам часто бывает удобно вместо адиабатической изоляции системы накладывать на ее поведение другие ограничения. Тогда критерии термодинамической устойчивости изменятся. Особенно удобны следующие критерии.
Критерий устойчивости для системы с постоянными объемом и энтропией.
Принимая во внимание соотношение (4) и первое начало термодинамики, можно написать:
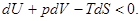(41)
При постоянстве энтропии и объема это дает
(42)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением внутренней энергии. Следовательно, устойчивым является состояние при минимуме внутренней энергии.
|
|
Критерий устойчивости для системы с постоянными давлением и энтропией. В этом случае условие (41) имеет вид
(43)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением энтальпии 
Следовательно, устойчивым является состояние при минимуме энтальпии.
Критерий устойчивости для системы с постоянными объемом и температурой. При 
и 
неравенство (41) записывается в виде
(44)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением свободной энергии 
Следовательно, устойчивым является лишь состояние при минимуме свободной энергии.
Критерий устойчивости для системы с постоянными температурой и давлением. С помощью выражения (17) для термодинамического потенциала неравенство (41) преобразуется к виду
(45)
При постоянных температуре и давлении дифференциалы 
и (45) сводятся к неравенству
(46)
т.е. в системе могут самопроизвольно происходить лишь процессы с уменьшением термодинамического потенциала. Следовательно, устойчивым является состояние при минимуме термодинамического потенциала Гиббса.