Задание по дисциплине «Математика» для студентов группы Б-11 на 27.03.2020, 1 пара.
Тема: Симметрия функций и преобразование их графиков.
Литература:
Алимов Ш.А., Колягин Ю.М.:«Алгебра и начала математического анализа.10-11 классы. 10-11 классы» -М.:Просвещение,2011.
https://docs.google.com/viewer?url=https%3A%2F%2Fs.11klasov.ru%2Findex.php%3Fdo%3Ddownload%26id%3D60%26viewonline%3D1
План работы:
- Изучить материал по теме.
- Выполнить задание
- Подписать свою работу.
- отправить работу в виде личного сообщения в сети ВКонтакте (Дина Соколова) до 12.00, 28.03.2020
Материал для самостоятельного изучения.
Наверняка многие из вас могут быстро и правильно построить графики некоторых функций, не прибегая к вычислениям значений точек. Всем известно, что график функции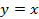 
– это прямая, а график функции 
– это парабола. Но как построить, например, график функции 
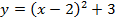, не вычисляя значения точек? Для этого существуют правила преобразования графиков функций.
Преобразование симметрии относительно оси Ox
Предположим, что у нас есть функция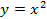 
(график этой функции – это парабола) и необходимо построить график функции 
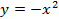. Вычислим значения некоторых точек для графиков этих функций.
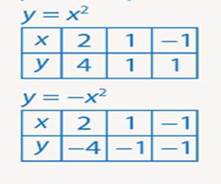
Из таблиц видно, что одним и тем же значениям аргумента соответствуют противоположные значения функций. Графически это означает, что графики расположены симметрично относительно оси абсцисс. То есть заданная парабола (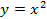) зеркально отобразится относительно оси 
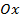(см. Рис. 1).
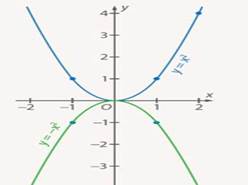
Рис. 1. Графики функци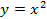й и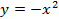
Таким образом, если у нас есть произвольный график 
, то для построения графика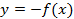 
необходимо график симметрично отразить относительно оси 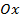(см. Рис. 2). Такое преобразование называется преобразованием симметрии относительно оси 
.
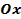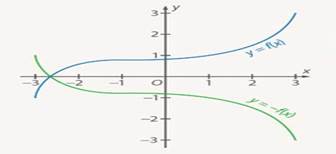
Рис. 2. Преобразование симметрии относительно оси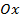
Преобразование симметрии – зеркальное отражение относительно прямой. График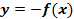 
получается из графика функции 
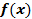преобразованием симметрии относительно оси 
.
На рисунке 3 показаны примеры симметрии относительно оси .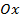
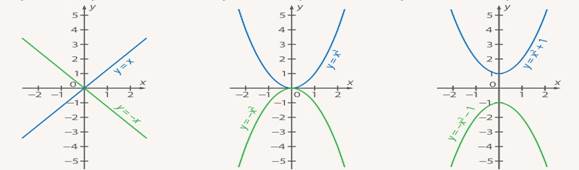
Рис. 3. Симметрия относительно оси Ox
Параллельный перенос вдоль оси Oy
Предположим, что у нас есть функция 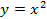(график этой функции – это парабола) и необходимо построить график функции 
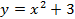. Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 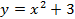больше на 3 единицы. Графически это означает, что график функции 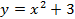находится на 3 единицы выше, чем график функции 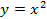(см. Рис. 4).
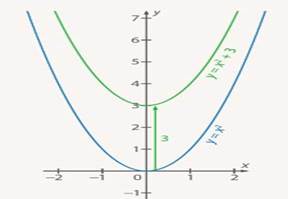
Рис. 4. Графики функци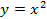й и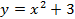
Растяжение от оси Ox и сжатие к оси Ox
Предположим, что у нас есть функция 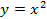(график этой функции – это парабола) и необходимо построить график функции 
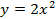. Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что при одних и тех же значениях аргумента значения функции у графика 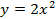больше в 2 раза. Графически это означает, что график функции 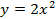сужается по сравнению с графиком функции 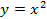(см. Рис. 7).
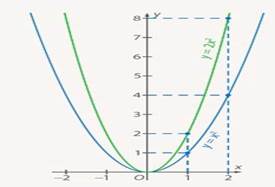
Рис. 7. Графики функци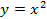й и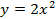
Параллельный перенос вдоль оси Ox
Предположим, что у нас есть функция 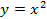, необходимо построить график функции 
. Вычислим значения некоторых точек для графиков этих функций.
Из таблиц видно, что одинаковым значениям функции соответствуют значения аргумента, отличающиеся на 2 единицы. Это означает, что график данной функции переместился на 2 единицы относительно оси ординат влево (см. Рис. 11), так как для получения одинаковых значений функций приходится брать значения аргумента на 2 меньше:
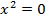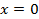
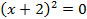, при 
при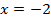 
Следовательно, если необходимо было построить график функции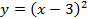 
, то сдвиг на 3 единицы относительно оси ординат был бы вправо (по сравнению с графиком функции 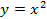) (см. Рис. 11).
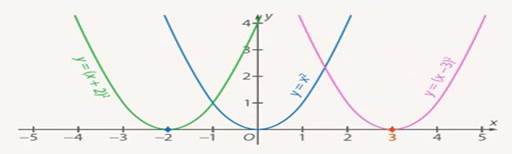
Рис. 11. Графики функци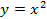й , и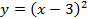
НАПРИМЕР. Построить график функции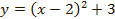 
.
Решение
Построим график заданной функции последовательно (см. Рис. 20):
1. Строим график .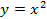
2. График 
получается из графика 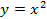параллельным переносом последнего на 2 единицы вправо.
3. График 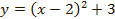получается из графика функции параллельным переносом последнего вдоль оси ординат на 3 единицы вверх.
Рис. 20. Иллюстрация к задаче
Мы могли бы сделать операции в обратном порядке, то есть сначала поднять график 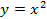на 3 единицы вверх, а потом получившийся график сдвинуть вправо на 2 единицы (см. Рис. 21).
Рис. 21. Иллюстрация к задаче
Обратите внимание, что не все графики функций можно строить в произвольном порядке. Например, для построения графика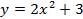 
сначала нужно построить график 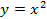, затем график 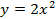(растяжение от оси 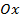), а далее – график 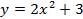(параллельный перенос вдоль оси ординат) (см. Рис. 22). Если же сделать в другой последовательности, то есть построить 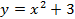, то далее на 2 придется умножить всё выражение.
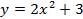
– ПРАВИЛЬНО
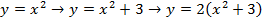– НЕПРАВИЛЬНО
ЗАДАНИЕ. Построить график функции: 