Г-8
Вписанные и описанные окружности. Решение задач.
Яндекс.Видео ›урок вписанные и описанные окружности
Описанная окружность.
О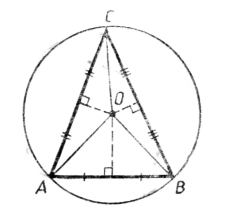 
пределение: Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник – вписанным в окружность.
Теорема. Около любого треугольника можно описать окружность и притом только одну.
В отличие от треугольника около четырехугольника не всегда можно описать окружность. Например: ромб.
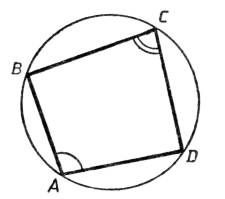
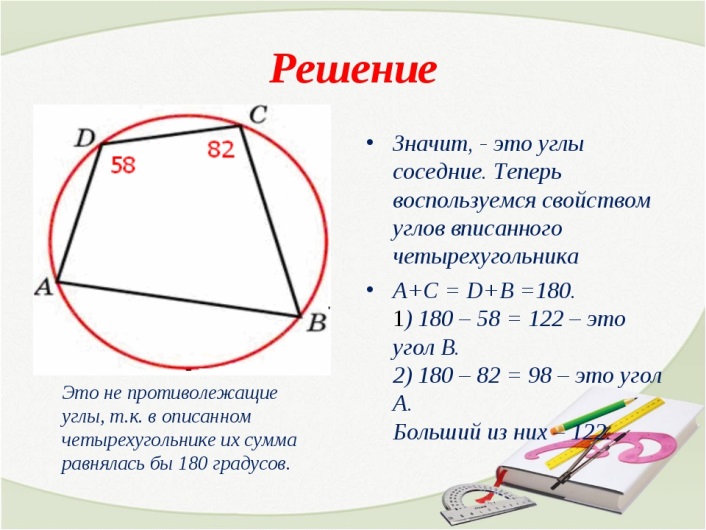
Теорема. В любом вписанном четырехугольнике сумма противоположных углов равна 1800.
Если сумма противоположных углов четырехугольника равна 1800, то около него можно описать окружность.
Для того чтобы четырехугольник АВСD был вписанным, необходимо и достаточно, выполнения любого из следующих условий:
· ABCD выпуклый четырехугольник и ∟ABD=∟ACD;
· Сумма двух противоположных углов четырехугольника равна 1800.
Центр окружности равноудален от каждой из его вершин и поэтому совпадает с точкой пересечения серединных перпендикуляров к сторонам многоугольника, а радиус равен расстоянию от центра до вершин.
Для треугольника: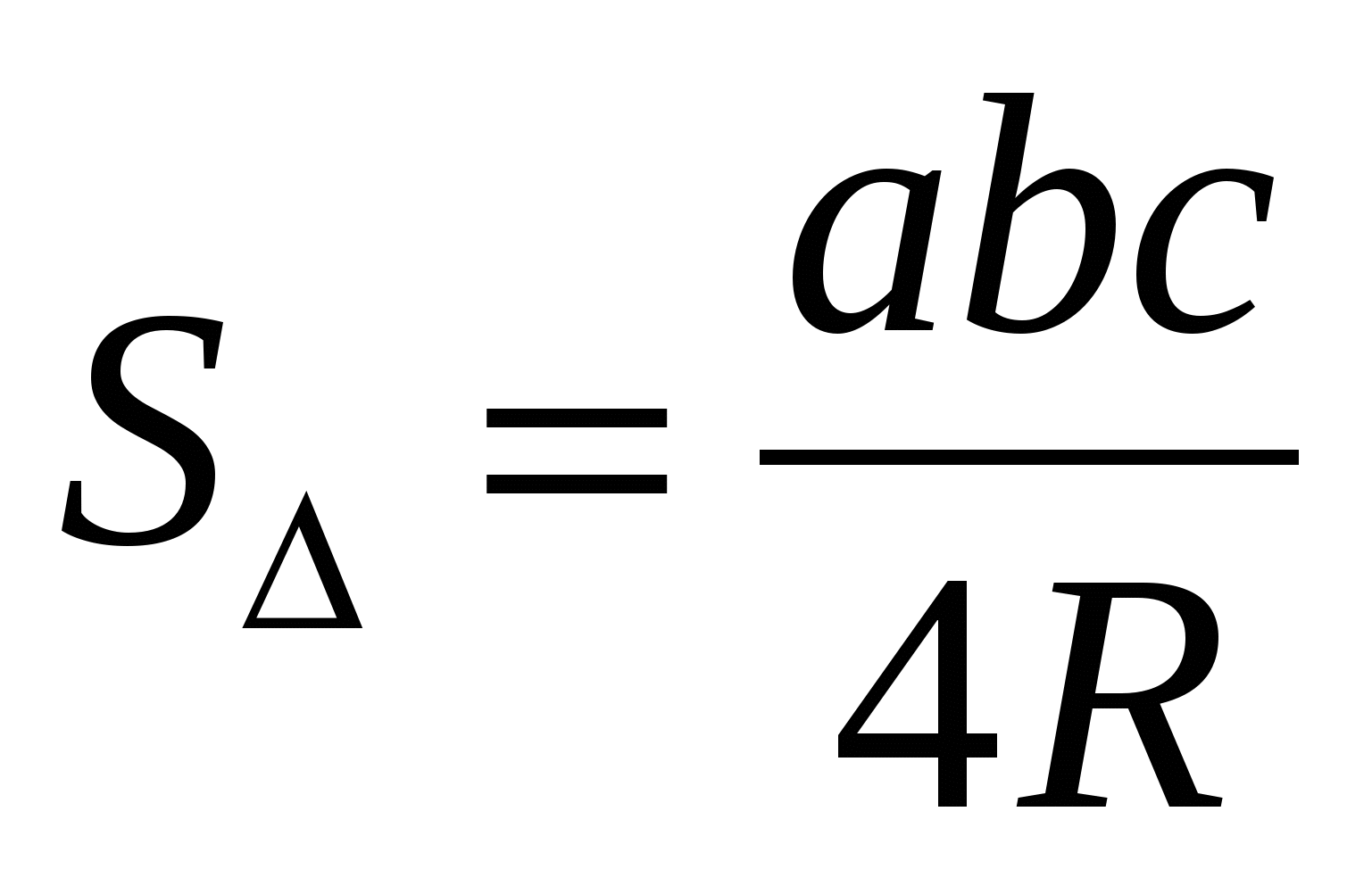 
Для правильного многоугольника: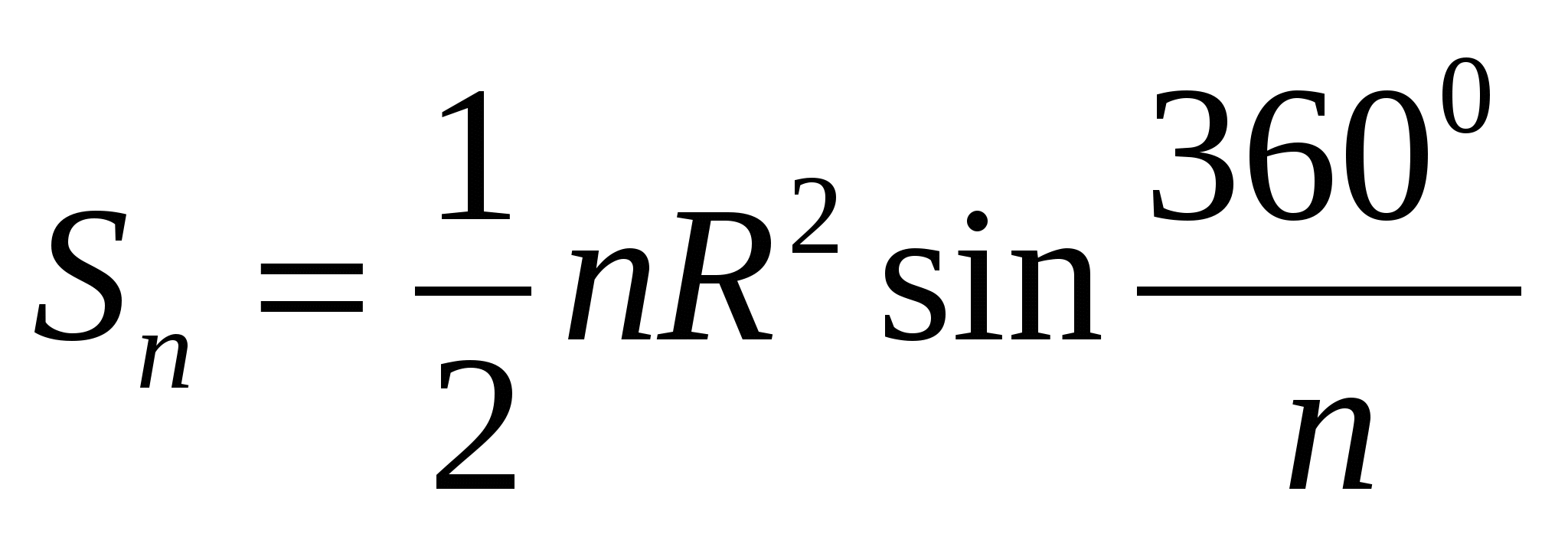 
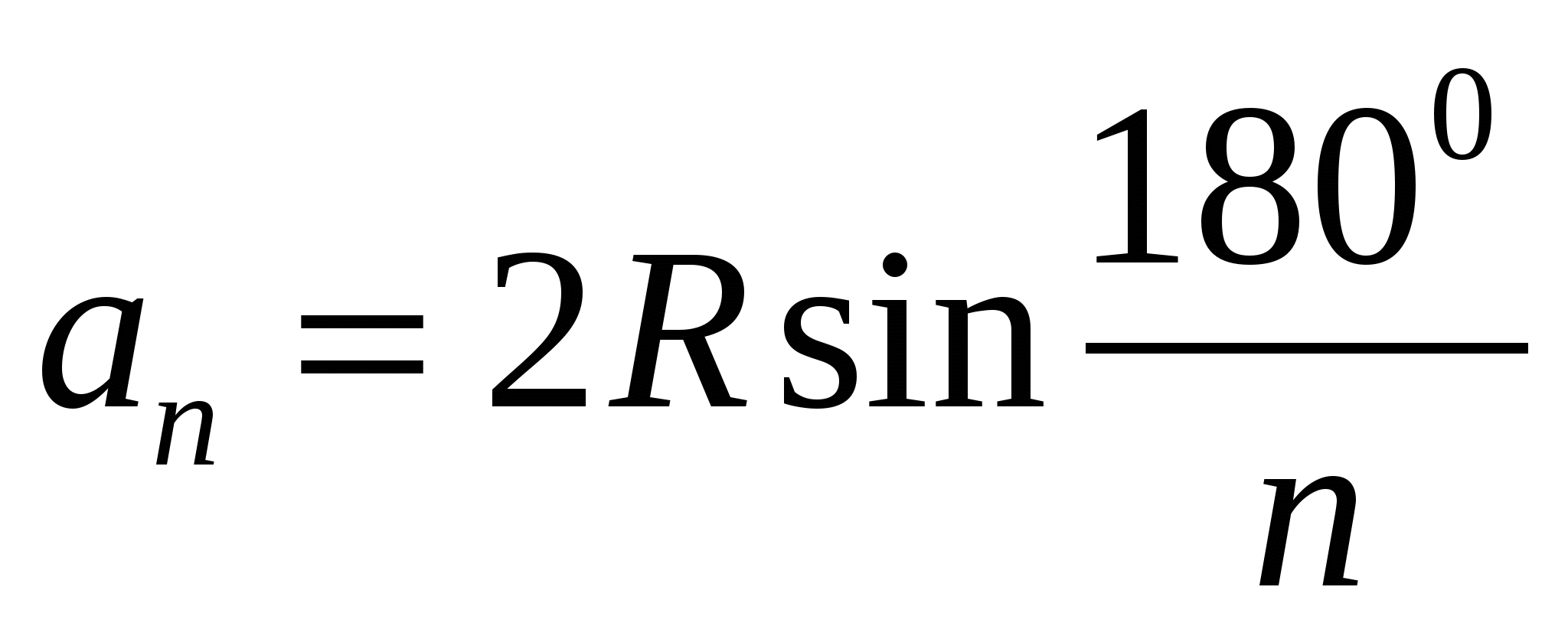
Вписанная окружность.
О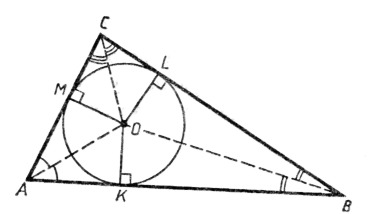 
пределение: Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник – описанным около этой окружности.
Теорема. В любой треугольник можно вписать окружность и притом только одну.
Не во всякий четырехугольник можно вписать окружность. Например: прямоугольник, не являющийся квадратом.
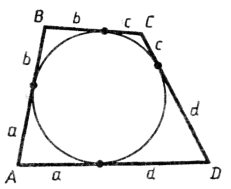
Теорема. В любом описанном четырехугольнике суммы длин противоположных сторон равны.
|
|
Если суммы длин противоположных сторон выпуклого четырехугольника равны, то в него можно вписать окружность.
Для того чтобы выпуклый четырехугольник ABCD являлся описанным, необходимо и достаточно, чтобы выполнялось условие AB+DC=BC+AD (суммы длин противоположных сторон равны).
Центр окружности равноудален от сторон многоугольника, значит, совпадает с точкой пересечения биссектрис углов многоугольника (свойство биссектрисы угла). Радиус равен расстоянию от центра окружности до сторон многоугольника.
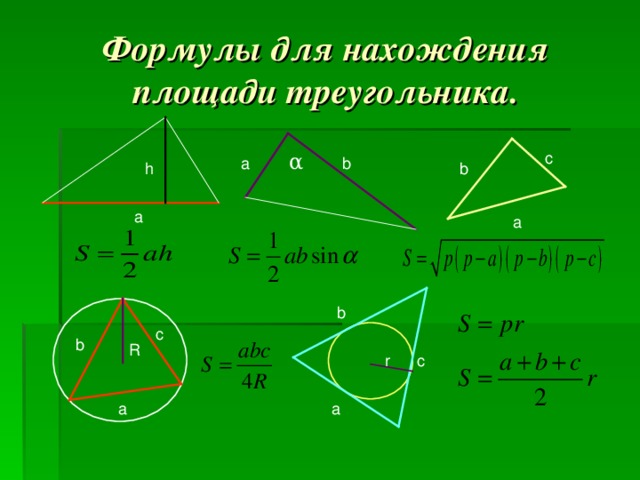
Задача 1.Через точку А окружности проведены диаметр АС и две хорды АВ и AD так, что хорда АВ равна радиусу окружности, точка D делит полуокружность АС на две равные дуги. Найдите углы четырехугольника ABCD, если точки С и D лежат по разные стороны от диаметра АС.
Решение: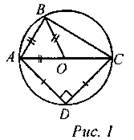 
1) ∠ABC = ∠ADC = 90°, как вписанные углы, опирающиеся на диаметр.
2) ∆АОВ - равносторонний, так как АО = ВО как радиусы, а хорда АВ равна радиусу, тогда ∠BAO = 60°, ∠BCO = 30°.
3) Точка D делит полуокружность АС на две равные дуги AD и DC, поэтому хорды AD и DC равны, то есть ∆ADC - равнобедренный прямоугольный, поэтому ∠DAC =∠DCA = 45°.
4) ∠BAD = ∠BAC + ∠DAC = 60° + 45° = 105°.
5) ∠BCD = ∠BCO + ∠DCA = 30° + 45° = 75°.
Задача 2.Основание равнобедренного треугольника равно 18 см, а высота, проведенная к нему, равна 12 см. Найдите радиусы вписанной в треугольник и описанной около треугольника окружностей.Решение:
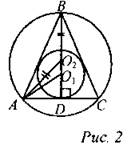∆AO2D - прямоугольный, по теореме Пифагора АО22 = AD2 + DO22. Точка O2 - центр описанной окружности - лежит на биссектрисе, медиане, высоте, а значит, на серединном перпендикуляре, проведенном к основанию.
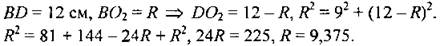 Центр вписанной окружности также лежит на BD. АО1 - биссектриса ∠BAC, следовательно АВ: ВО1 = AD: DO1. По теореме Пифагора в ∆ABD: АВ2 = AD2 + BD2 = 81 + 144 = 225, значит, АВ = 15 см. Так как ВO2 = R, то:
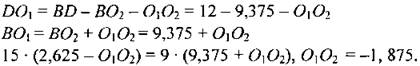Так как O1O2 < 0 => О1 лежит между точками В и O2, тогда DO1 - O1O2 = 2,625 + 1,875 = 4,5 см
|
|
|
Домашнее задание: Выучить конспект, разобрать задачи, просмотреть презентацию;
Отправить на эл. почту: тест из презентации и решение задач п.77, 78; № 690, 692, 693; доп. № 702