Номер варианта задания определяется последней цифрой зачетной книжки студента.
Задача 1 (Тема 2)
Фирма принимает заказы по телефону. Если в момент поступления заявки хотя бы один менеджер, принимающий заявки, свободен либо число заявок, ожидающих в очереди, не превосходит 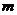 , заявка принимается. В противном случае заявка теряется. Известно, что в среднем поступает
, заявка принимается. В противном случае заявка теряется. Известно, что в среднем поступает 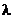 звонков в час, среднее время обслуживания одной заявки составляет
звонков в час, среднее время обслуживания одной заявки составляет 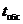 минут. Доход, получаемый фирмой в результате обслуживания одной заявки, в среднем равен
минут. Доход, получаемый фирмой в результате обслуживания одной заявки, в среднем равен 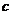 ден.ед., а менеджеру по продажам платят
ден.ед., а менеджеру по продажам платят 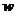 ден.ед. в час. Требуется определить количество менеджеров, при котором прибыль фирмы максимальна.
ден.ед. в час. Требуется определить количество менеджеров, при котором прибыль фирмы максимальна.
Значения параметров 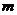 ,
, 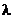 ,
, 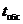 ,
, 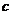 и
и 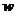 приведены в табл. 1.
приведены в табл. 1.
Таблица 1
| Параметры | Номер варианта | |||||||||
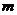
| ||||||||||
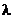
| ||||||||||
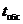
| 3,3 | 3,6 | 2,7 | 4,2 | 2,4 | 2,1 | 3,9 | 4,8 | 5,4 | 5,1 |
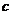
| 5,5 | 4,5 | 3,5 | 6,5 | 8,5 | |||||
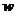
| 3,3 | 3,6 | 2,7 | 4,2 | 2,4 | 2,1 | 3,9 | 4,8 | 5,4 | 5,1 |
Задача 2 (Тема 3)
Фирма использует продукцию пяти видов. Годовой спрос на товар вида 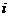 равен
равен 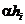 единиц товара. Издержки размещения заказа и содержания запасов составляют
единиц товара. Издержки размещения заказа и содержания запасов составляют 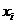 и
и 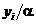 ден. ед., соответственно. Расход складской площади на единицу товара вида
ден. ед., соответственно. Расход складской площади на единицу товара вида 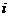 равен
равен 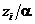 кв.м. Общая величина площади складских помещений равна 260 кв.м. Требуется определить оптимальные партии поставок при ограничении на максимальный уровень запаса, а также оценить уменьшение общих расходов на размещение заказов и содержание запасов при увеличении складских помещений на 10 кв.м.
кв.м. Общая величина площади складских помещений равна 260 кв.м. Требуется определить оптимальные партии поставок при ограничении на максимальный уровень запаса, а также оценить уменьшение общих расходов на размещение заказов и содержание запасов при увеличении складских помещений на 10 кв.м.
Значения параметров 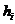 ,
, 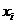 ,
, 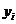 ,
, 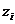 . приведены в табл. 2. Значение параметра
. приведены в табл. 2. Значение параметра 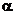 определяется формулой:
определяется формулой: 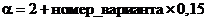 .
.
Таблица 2
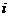
| 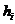
| 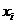
| 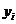
| 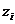
|
| 1,5 |
Задача 3 (Тема 3)
Распределение спроса на используемую фирмой продукцию за время выполнения заказа дискретно и задано в табл. 3. Продукция поставляется в среднем один раз в 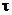 дней, издержки хранения одной единицы продукции в течение одного дня составляют
дней, издержки хранения одной единицы продукции в течение одного дня составляют 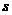 ден.ед., а издержки, связанные с дефицитом одной единицы продукции, равны
ден.ед., а издержки, связанные с дефицитом одной единицы продукции, равны 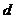 ден.ед. Требуется определить оптимальные страховой запас и точку размещения заказа (при которых суммарные издержки, связанные с содержанием страхового запаса и с дефицитом, минимальны), а также средний уровень дефицита, издержки содержания страхового запаса и потери, связанные с дефицитом (при найденных оптимальных страховом запасе и точке размещения заказа).
ден.ед. Требуется определить оптимальные страховой запас и точку размещения заказа (при которых суммарные издержки, связанные с содержанием страхового запаса и с дефицитом, минимальны), а также средний уровень дефицита, издержки содержания страхового запаса и потери, связанные с дефицитом (при найденных оптимальных страховом запасе и точке размещения заказа).
Значения параметров 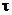 ,
, 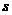 и
и 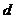 приведены в табл. 4.
приведены в табл. 4.
Таблица 3
| Спрос (в единицах продукции) | |||||||
| Вероятность | 0,05 | 0,1 | 0,2 | 0,3 | 0,2 | 0,1 | 0,05 |
Таблица 4
| Параметры | Номер варианта | |||||||||
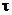
| ||||||||||
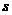
| 0,33 | 0,36 | 0,25 | 1,14 | 1,22 | 0,50 | 0,24 | 0,77 | 0,88 | 0,55 |
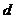
|
Задача 4 (Тема 4)
Издержки фирмы на производство продукции составляют 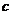 денежных единиц в расчете на 1 единицу продукции. Фирма реализует продукцию по цене
денежных единиц в расчете на 1 единицу продукции. Фирма реализует продукцию по цене 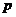 ден.ед. Непроданный товар реализуется по сниженной цене, равной
ден.ед. Непроданный товар реализуется по сниженной цене, равной 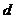 ден.ед. Спрос может составлять
ден.ед. Спрос может составлять 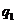 ,
, 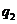 ,
, 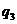 и
и 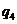 шт. Определить оптимальное количество производимой продукции с помощью критериев Лапласа, Вальда, Сэвиджа и Гурвица (при заданном значении параметра
шт. Определить оптимальное количество производимой продукции с помощью критериев Лапласа, Вальда, Сэвиджа и Гурвица (при заданном значении параметра 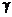 ).
).
Значения параметров 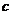 ,
, 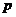 ,
, 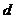 ,
, 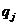 (где
(где 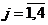 ) и
) и 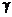 приведены в табл. 4.
приведены в табл. 4.
Таблица 4
| Параметры | Номер варианта | |||||||||
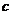
| ||||||||||
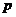
| 25,5 | 34,5 | 43,5 | 40,5 | 16,5 | |||||
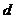
| 15,3 | 12,6 | 10,8 | 16,2 | 20,7 | 26,1 | 24,3 | 14,4 | 7,2 | 9,9 |
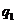
| ||||||||||
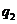
| ||||||||||
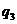
| ||||||||||
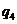
| ||||||||||
| γ | 0,51 | 0,42 | 0,36 | 0,54 | 0,69 | 0,87 | 0,81 | 0,48 | 0,24 | 0,34 |
Задача 5 (Тема 5)
Осуществление проекта требует выполнения ряда работ. Номера работ, их продолжительности и перечни работ, которые должны быть закончены к началу выполнения других работ, приведены в табл. 5.
Требуется:
1) построить сетевой график выполнения работ;
2) рассчитать минимальное время выполнения всего комплекса работ;
3) определить ранние и поздние сроки начала и окончания работ, и их полные и свободные резервы времени;
4) найти критические работы и построить критический путь (на сетевом графике).
Таблица 5
| Номера работ | Предше-ствующие работы | Продолжительность работы, дн. | |||||||||
| Номер варианта | |||||||||||
| – | |||||||||||
| – | |||||||||||
| 4, 5 | |||||||||||
| 4, 5 | |||||||||||
| 3, 6 |
Задача 6 (тема 6)
Начальные инвестиции в проект равны 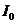 , коэффициент прибыли –
, коэффициент прибыли – 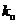 для всех лет, коэффициент реинвестирования –
для всех лет, коэффициент реинвестирования – 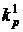 для первого года,
для первого года, 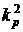 для второго года, и
для второго года, и 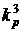 для всех последующих лет (начиная с третьего). Внутренняя доходность альтернативных проектов – r. (Значения приведены в табл. 6.)
для всех последующих лет (начиная с третьего). Внутренняя доходность альтернативных проектов – r. (Значения приведены в табл. 6.)
Требуется:
1) определить свободные денежные потоки для первого, второго и третьего лет;
2) оценить рыночную стоимость проекта в начале третьего года;
3) определить текущую и чистую текущую стоимости проекта;
4) записать уравнение для определения внутренней доходности проекта и решить это уравнение на ЭВМ средствами Excel.
Таблица 6
| Номер варианта | ||||||||||
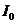
| ||||||||||
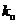
| 40% | 25% | 30% | 35% | 45% | 42% | 32% | 28% | 34% | 36% |
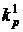
| 91% | 83% | 70% | 87% | 82% | 95% | 92% | 74% | 65% | 62% |
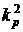
| 72% | 64% | 65% | 67% | 53% | 45% | 38% | 63% | 52% | 48% |
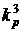
| 24% | 30% | 28% | 22% | 15% | 12% | 14% | 18% | 19% | 17% |
| r | 26% | 19% | 24% | 25% | 22% | 23% | 27% | 18% | 28% | 23% |
Задача 7 (Тема 8)
Данные о рыночной цене коттеджей (которые строит фирма), а также об их площади, вместимости гаража и количестве комнат приведены в таблицах 7, 8 и 9.
Требуется:
1) построить линейную регрессионную модель для оценки рыночной стоимости коттеджей, и с помощью этой модели оценить рыночную стоимость коттеджа с 4 комнатами, площадью 200 кв.м., и с вместимостью гаража – 1 автомобиль;
2) с помощью t -статистик проверить гипотезы о незначимости каждого в отдельности объясняющего фактора при уровне значимости 0,1.
3) С помощью F -статистики проверить гипотезу о незначимости всех объясняющих факторов одновременно при уровне значимости 0,1.
4) Выбрать объясняющие факторы, обеспечивающие наибольшее значение скорректированного коэффициента детерминации и с помощью соответствующей модели оценить рыночную стоимость коттеджа с характеристиками, приведенными в п.1.
Таблица 7
| Номер наблюдения | Цена, ден.ед. | |||||||||
| Номер варианта | ||||||||||
Таблица 8
| Номер наблю-дения | Площадь, кв.м. | |||||||||
| Номер варианта | ||||||||||
| 111,1 | 107,8 | 112,2 | 123,2 | 118,8 | 127,6 | 124,3 | 117,7 | 113,3 | 128,7 | |
| 116,15 | 112,7 | 117,3 | 128,8 | 124,2 | 133,4 | 129,95 | 123,05 | 118,45 | 134,55 | |
| 141,4 | 137,2 | 142,8 | 156,8 | 151,2 | 162,4 | 158,2 | 149,8 | 144,2 | 163,8 | |
| 171,7 | 166,6 | 173,4 | 190,4 | 183,6 | 197,2 | 192,1 | 181,9 | 175,1 | 198,9 | |
| 181,8 | 176,4 | 183,6 | 201,6 | 194,4 | 208,8 | 203,4 | 192,6 | 185,4 | 210,6 | |
| 191,9 | 186,2 | 193,8 | 212,8 | 205,2 | 220,4 | 214,7 | 203,3 | 195,7 | 222,3 | |
| 191,9 | 186,2 | 193,8 | 212,8 | 205,2 | 220,4 | 214,7 | 203,3 | 195,7 | 222,3 | |
| 212,1 | 205,8 | 214,2 | 235,2 | 226,8 | 243,6 | 237,3 | 224,7 | 216,3 | 245,7 | |
| 212,1 | 205,8 | 214,2 | 235,2 | 226,8 | 243,6 | 237,3 | 224,7 | 216,3 | 245,7 | |
| 232,3 | 225,4 | 234,6 | 257,6 | 248,4 | 266,8 | 259,9 | 246,1 | 236,9 | 269,1 |
Таблица 9
| Номер наблюдения | Вместимость гаража | К-во комнат |
Задача 8 (Тема 11)
Значения спроса на продукцию фирмы за каждый месяц в течение двух лет приведены в таблице 10. Требуется построить прогноз спроса для первых трех месяцев следующего года методом скользящего среднего (при этом необходимо определить оптимальные весовые коэффициенты и их количество).
Таблица 10
| Месяцы | Спрос | |||||||||
| Номер варианта | ||||||||||
Задача 9 (Тема 11)
Значения спроса на продукцию за каждый квартал в течение пяти лет приведены в таблице 11. Требуется построить поквартальный прогноз спроса для следующего года следующими методами:
– экспоненциального сглаживания;
– Холта (с учетом тренда);
– Винтера (с учетом тренда и сезонных колебаний).
Таблица 11
| Квартал | Спрос | |||||||||
| Номер варианта | ||||||||||