На эпюре Монжа без особого труда можно изобразить точку или прямую, но как поступить при изображении плоскости, которая полностью перекрывает обе плоскости проекций? При проецировании точек плоскости на плоскости проекций получается два плоских поля точек, причем каждой точке одного поля проекций соответствует единственная точка другого поля проекций, а каждой прямой – единственная прямая. При совмещении плоскостей проекций оба поля точек накладываются друг на друга, но соответствие не нарушается, и все пары соответственных точек лежат на общих линиях связи. Каждая плоскость устанавливает единственное ей присущее соответствие. Такое соответствие в проективной геометрии называется аффинной гомологией (родственным соответствием или перспективно-аффинным преобразованием). Возникает вопрос, сколько же необходимо пар точек или прямых, чтобы задать плоскость? Набор элементов, необходимый для выделения геометрического образа, называется репером. Положение плоскости в пространстве определяется тремя точками, точкой и прямой или двумя пересекающимися прямыми, причем они могут пересекаться и в несобственной точке, т.е. параллельны. Отсюда вытекает три способа задания плоскости на эпюре Монжа (рис. 2.8, а, б и в). Способы задания плоскости взаимно связаны между собой: можно перейти от одного способа задания к другому.
При задании плоской кривой линии или иной плоской фигуры произвольно выбирается только одна проекция, а на другой проекции указывается не более трех точек, остальные точки определяются построением с соблюдением условия принадлежности точки плоскости. Если плоскость задана, то по одной из проекций точки, принадлежащей плоскости, можно построить единственную соответствующую ей недостающую проекцию этой точки. Алгоритм построения недостающей проекции основан на условии принадлежности точки и прямой плоскости: точка принадлежит плоскости, если она принадлежит прямой этой плоскости, прямая принадлежит плоскости, если она проходит хотя бы через две точки этой плоскости.
а) б) в)

Рис. 2.8. Способы задания плоскости:
а – тремя точками, б – точкой и прямой, в – двумя параллельными или пересекающимися прямыми
В плоскости выделяют особые линии: горизонтали, фронтали и следы плоскости (рис.2.10).
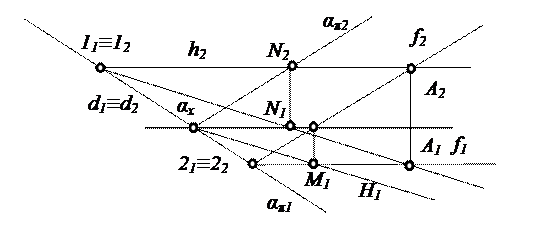
Рис. 2.10. Особые линии в плоскости
Горизонталью плоскости h называется прямая линия, лежащая в плоскости и параллельная горизонтальной плоскости проекций. Фронталью плоскости f называется прямая линия, лежащая в плоскости и параллельная фронтальной плоскости проекций. Все горизонтали и фронтали плоскости соответственно параллельны между собой. Построение горизонтали плоскости начинается с фронтальной проекции, а фронтали – с горизонтальной проекции. Горизонталь и фронталь плоскости, лежащие в плоскостях проекций и являющиеся линиями пересечения заданной плоскости с плоскостями проекций называются следами плоскости. Для нахождения следов плоскости достаточно построить следы двух прямых, принадлежащих плоскости. Любая плоскость пересекает тождественную плоскость τ по некоторой прямой линии d. Значит, в любой плоскости существует двойная прямая линия, все точки которой имеют на эпюре совпадающие проекции. Точка пересечения следов αх,, лежащая на оси проекций (точка пересечения трех плоскостей: α, π1 и π2), называется точкой схода следов. Точка схода является двойной точкой.
Особый интерес представляют плоскости, занимающие частное положение относительно проекционного аппарата (рис. 2.11). Плоскости, проходящие через центры проецирования, перпендикулярные к плоскостям проекций и содержащие семейства проецирующих прямых, называются проецирующими. Проецирующие плоскости моделируются на эпюре Монжа вырожденным соответствием, так как точки и фигуры, принадлежащие этим плоскостям, проецируются в прямую линию. Это важное собирательное свойство проектирующих плоскостей используется при решении задач на пересечение геометрических образов.
Горизонтально проецирующая плоскость проходит через центр проецирования S1 перпендикулярно к горизонтальной плоскости проекций (рис. 2.11, а). Всё семейство фронталей этой плоскости является горизонтально проецирующими прямыми.
а) б) в)

г) д) е)

Рис. 2.11. Плоскости частного положения:
а – горизонтально проецирующая, б – фронтально проецирующая, в – профильно проецирующая, г – горизонтальная, д – фронтальная, е – профильная
Фронтально проецирующая плоскость проходит через центр проецирования S2 перпендикулярно к фронтальной плоскости проекций (рис. 2.11, б). Всё семейство горизонталей этой плоскости является фронтально проецирующими прямыми. Горизонтали и фронтали профильно проецирующей плоскости совпадают (рис. 2.11, в). Плоскости, параллельные плоскостям проекций, называют плоскостями уровня: горизонтальная (рис. 2.11, г), фронтальная (рис. 2.11, д) и профильная (рис. 2.11, е) плоскости. Фигуры, расположенные в плоскостях уровня, изображаются в натуральную величину. Плоскости уровня являются дважды проецирующими. Профильная плоскость вырождаются в прямую, совпадающую с линией связи. Для выполнения каких-либо построений в профильной плоскости необходима дополнительная проекция.
В пирамиде (рис.2.6 и 2.7) грань ABC занимает горизонтальное положение, грань ACS занимает фронтальное положение, грань ABS занимает профильное положение, грань BCS занимает общее положение.
Многогранники образуются в результате взаимного пересечения плоскостей. Две произвольные плоскости образуют двугранный угол. Три плоскости определяют трехгранный угол. Четыре произвольные плоскости ограничивают часть пространства и задают тетраэдр. Наибольшее распространение среди многогранников имеют призмы и пирамиды. Призмой называется многогранник, у которого две грани (одинаковые многоугольники) являются основаниями, а остальные боковые грани пересекаются по параллельным прямым (ребрам). Если ребра призмы перпендикулярны основанию, то она называется прямой, в противном случае – наклонной. В основаниях призмы могут быть правильные и неправильные многоугольники. Если в основании призмы лежит треугольник, то она называется треугольной призмой, если четырехугольник, то – четырехугольной призмой и.т.п. Пирамидой называется многогранник, у которого одна грань является основанием (любой многоугольник), а остальные боковые грани имеют общую вершину. Если все грани треугольной пирамиды являются равносторонними одинаковыми треугольниками, то она называется правильным тетраэдром.
Существует только пять правильных многогранников. Тетраэдр, гексаэдр или куб, октаэдр, икосаэдр и додекаэдр – правильные многогранники (тела Платона). Вокруг каждого правильного многогранника можно описать сферу. Многогранник, у которого все грани равны и представляют собой правильные многоугольники с равными углами и сторонами, называется правильным. Тетраэдр состоит из четырех плоскостей (равносторонних треугольников), шести ребер и четырех вершин. В каждой вершине сходятся три ребра. Гексаэдр имеет шесть плоскостей (квадратов), двенадцать ребер и восемь вершин. В каждой вершине сходятся три ребра. Октаэдр состоит из восьми плоскостей (равносторонних треугольников), двенадцати ребер и шести вершин. В каждой вершине сходятся четыре ребра. Икосаэдр состоит из двадцати плоскостей (равносторонних треугольников), тридцати ребер и двенадцати вершин. В каждой вершине сходятся пять ребер. Додекаэдр состоит из двенадцати граней (правильных пятиугольников), тридцати ребер и двадцати вершин. В каждой вершине сходятся три ребра. Поверхность любого многогранника состоит из конечного числа плоских многоугольников. Различают выпуклые и звездчатые (вогнутые) многогранники. Многогранник называется выпуклым, если расположен по одну строну от плоскости любой грани. Для правильного изображения многогранников, необходимо умение строить проекции плоских фигур – многоугольников.