Итоговый тест по дисциплине «Численные методы»

13.06.2020. 13.06.2020.

Вопросы, которые нужно повторить.

Экзамен будет проходить в виде теста.

Потренироваться можно на пробных тестах. Файлик с тестами ниже.

3.

Теоретический и практический материал можно вспомнить здесь

(это мы все с вами делали в практических работах)

https://drive.google.com/file/d/1pKsSPI1jmfv2_57UXyjIoEUNg8TG9BJx/view?usp=sharing

4. А можно и здесь: https://www.intuit.ru/studies/courses/2317/617/info

1. Приближенные числа и действия над ними.

2. Приближенные значения. Абсолютная и относительная погрешность. Верные и значащие цифры.

3. Представление чисел в ЭВМ. Вычисление погрешностей арифметических действий.

4. Учет погрешностей вычислений по заданной формуле. Вычисления по правилам подсчета цифр.

5. Вычисления со строгим учетом предельных абсолютных погрешностей.

6. Вычисления по методу границ.

7. Отделение и уточнение корня уравнения методом половинного деления.

8. Метод простой итерации для решения уравнений.

9. Нахождение корня уравнения методом касательных.

10. Нахождение корня уравнения методом хорд.

11. Нахождение корня уравнения методом хорд и касательных.

12. Решение систем линейных алгебраических уравнений (СЛАУ) численными методами. Метод Гаусса.

13. Метод простой итерации для системы линейных алгебраических уравнений (СЛАУ).

14. Интерполяционный многочлен Лагранжа.

15. Первая интерполяционная формула Ньютона.

16. Вторая интерполяционная формула Ньютона.

17. Экстраполирование функций.

18. Численное интегрирование. Квадратурные формулы Ньютона-Котеса.

19. Численное интегрирование. Формулы трапеций.

20. Численное интегрирование. Формула Симпсона.

21. Численные методы решения обыкновенных дифференциальных уравнений. Метод Эйлера.

22. Численные методы решения обыкновенных дифференциальных уравнений. Метод Рунге-Кутта.

23. Численное решение задач оптимизации.

24. Поиск минимума функции одной переменной.

25. Поиск минимума функции многих переменных.

 

 

Примерные тесты

Итоговый тест по дисциплине «Численные методы»

 

1. В чем выражается обычно относительная погрешность?

А) В процентах (%)

Б) В процентах на единицу (%/ед.)

В) В штуках (шт)

Г) В х (х)

 

1. К несуществующим видам погрешностей относится

А) Неустранимая погрешность

Б) Погрешность метода

В) Вычислительная погрешность

Г) Результирующая погрешность

 

1. Предельная относительная погрешность произведения находится по формуле

А)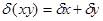

Б)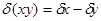

В)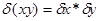

С)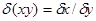

 

1. В чем заключается задача отделения корней?

А) В установлении количества корней

Б) В установлении количества корней, а так же наиболее тесных промежутков, каждый из которых содержит только один корень.

В) В установлении корня решения уравнения

Г) В назначении количества корней

 

1. К методам уточнения корней не относится …

А) Метод дихотомии

Б) Метод хорд

В) Метод касательных

Г) Метод аппроксимации

 

1. Суть комбинированного метода хорд и касательных?

А) Метод хорд и касательных дают приближения к корню с разных сторон.

Б) При реализации метода при каждой итерации необходимо вычислять не только значения F(x), но и ее производной.

В) Метод ограничивается вычислениями только значения F(x).

Г) Нет правильного ответа

 

1. К какой категории методов вычислительной математики относиться метод Гаусса?

А) Относится к первому классу точных задач.

Б) Относится ко второму классу приближенных методов.

В) Относится к точным методам.

Г) Относится к приближенным задачам.

 

1. Невязка – это…

А) Значение разностей между свободными членами исходной системы.

Б) Значение суммы между свободными членами исходной системы и результатами подстановки в уравнения системы найденных значений неизвестных

В) Значение суммы результатов подстановки в уравнения системы найденных значений неизвестных

Г) Значение разностей между свободными членами исходной системы и результатами подстановки в уравнения системы найденных значений неизвестных.

 

9. Задачу построения приближающей функции в общем смысле называют?

А) Равномерной

Б) Интерполяцией

В)Аппроксимацией

Г) Нет правильного ответа

 

1. Интерполяция – это…

А) Способ нахождения промежуточных значений величины по имеющемуся дискретному набору известных значений

Б) Продолжение функции, принадлежащей заданному классу, за пределы ее области определения.

В) Замена одних математических объектов другими, в том или ином смысле близким к исходным.

Г) Метод решения задач, при котором объекты разного рода объединяются общим понятием.

 

1. Интерполяция бывает:…

А) Кусочная и локальная

Б) Локальная и глобальная

В) Кусочная и априорная

Г) Максимальная пи минимальная

 

1. Итерация – это ….

А) Повторение. Результат повторного применения какой–либо математической операции.

Б) Замена одних математических объектов другими, в том или ином смысле близким к исходным.

В) Число, изображаемое единицей и 18 нулями

Г) Продолжение функции, принадлежащей заданному классу, за пределы ее области определения.

 

13. Найди в формуле интерполяционного многочлена Лагранжа ошибку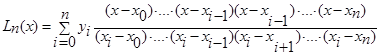

 

А)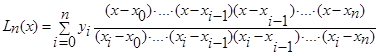

Б )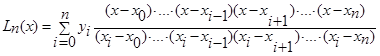

В)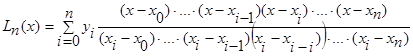

Г ) Нет ошибки в формуле

 

14. Конечными разностями первого порядка называют

А) Сумму соседних узлов интерполяций

Б ) Разность между значениями функций в соседних узлах интерполяции

В) Сумму между значениями функций в соседних узлах интерполяции

Г) Произведение значений трех соседних узлов интерполяции

 

 

15. Что это за формула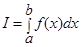

А) Формула Ньютона - Лейбница

Б) Формула Ньютона - Котеса

В) Формула Симпсона

Г) Формулы не существует

 

 

16. Формула Симпсона – это…

А)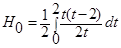

Б)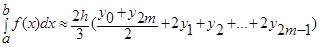

В)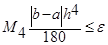

Г) Формулы не существует

 

1. В основе какого метода лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной форме?

А) Метод Лагранжа

Б) Метод границ

В) Метод Коши

Г) Метод Эйлера

 

1. Формула Рунге-Кутта это:

А)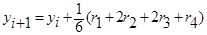

Б)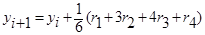

В)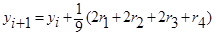

Г)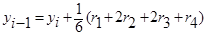

 

1. Что является решением дифференциального уравнения?

А) Уравнение первого порядка

Б) Уравнение первого порядка, разрешенное относительно производной

В) Уравнение второго порядка

Г) Уравнение второго порядка, разрешенное относительно производной

 

1. Золотое сечение – это…

А) Такое пропорциональное деление отрезка на части, при котором меньший отрезок относится к большему, как больший ко всему.

Б) Непропорциональное деление отрезка на части, при котором меньший отрезок относится к большему, как больший ко всему.

В) Непропорциональное деление отрезка на части, при котором больший отрезок относится к меньшему, как больший ко всему.

Г) Такое пропорциональное деление отрезка на части, при котором больший отрезок относится к меньшему, как больший ко всему.

 

1. Формула золотого сечения при решении минимизации?

А)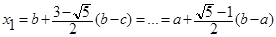

Б)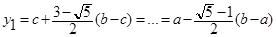

В)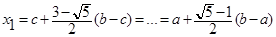

Г)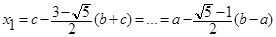

 

1. Пусть а=2,91385 и 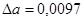. Тогда в числе а верны в широком смысле:

 

А) 2,9,1

Б) 2,9

В) 9,1

Г) Все цифры

 

1. Погрешность разности чисел x=62,425 и y=62,409, у которых все числа верны в строгом смысле, равна

 

А) 0,09

Б) 1

В) 0,07

Г) 0,12

 

1. Уравнение 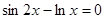имеет единственный корень на отрезке:

 

А) [1; 1.5]

Б) [0; 0.5]

В) [-1;1]

Г) [-1; 0.5]

 

1. Решением системы линейных уравнений 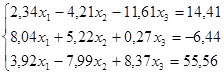будет

 

А) (0,967; -4,816; 2,293)

Б) (0;0;0)

В) (0,25;0,15;-0,12)

Г) (-11;0;2)