Функция распределения дискретной случайной величины

Лекция 4

Дискретные случайные величины

 

Случайная величина называется дискретной (постоянной), если она может принимать отдельные изолированные возможные значения.

Законом распределения дискретной случайной величины называется соотношение между ее возможными значениями и их вероятностями. Закон распределения может быть задан формулой, таблицей или графиком.

Биноминальным называют закон распределения дискретной случайной величины Х – числа появлений события в n независимых испытаниях, в каждом из которых вероятность появления события равна p; вероятность возможного значения Х = k (числа k появлений события) вычисляют по формуле Бернулли:

Числовые характеристики дискретных случайных величин

Характеристикой среднего значения случайной величины служит математическое ожидание. Математическим ожиданием дискретной случайной величины называют сумму произведений всех её возможных значений на их вероятности: где суммирование ведётся по всем возможным значениям.

Математическое ожидание биноминального распределения равно произведению числа испытаний на вероятность появления события в одном испытании .

Характеристиками рассеивания возможных значений вокруг математического ожидания служат дисперсия и среднее квадратичное отклонение.

Дисперсией случайной величины Х называют отклонения математического ожидание квадрата случайной величины от квадрата её математического ожидания:

Дисперсия биноминального распределения равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании .

Средним квадратичным отклонением случайной величины называется корень квадратный из дисперсии, взятый со знаком «+»:

.

Функция распределения дискретной случайной величины

Функцией распределения называется функция, определяющая для каждого значения x вероятность того, что величина X примет значение меньшее x:

,

(здесь 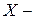случайная величина, а действительные числа, в том числе возможные значения случайной величины).

 

Свойства функции распределения:

1.

2. неубывающая функция,

3.

4. Если то .

5. непрерывна слева, т.е.

 

Пример 1. Автобус проходит мимо остановки «по требованию» 5 раз в день. Вероятность остановки автобуса . Составить закон распределения случайной величины в виде числа остановок автобуса в день, найти и построить график функции распределения.

Решение. По условию задачи мы имеем дело со схемой Бернулли повторных независимых испытаний с постоянной вероятностью события в каждом испытании. Случайная величина 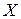– число остановок автобуса в день – описывается законом биномиального распределения (формулой Бернулли):

Закон распределения в виде формулы имеет вид:

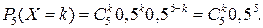
Возможные значения случайной величины – 0, 1, 2, 3, 4 и 5. Найдем их вероятности и занесем их в таблицу вместе с возможными значениями:

Закон распределения в виде таблицы получен.

Контроль:

В таблицу мы дополнительно ввели строку для квадратов возможных значений, которые понадобятся нам для вычисления дисперсии.

Вычислим математическое ожидание, дисперсию и среднее квадратичное отклонение.

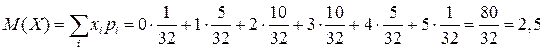
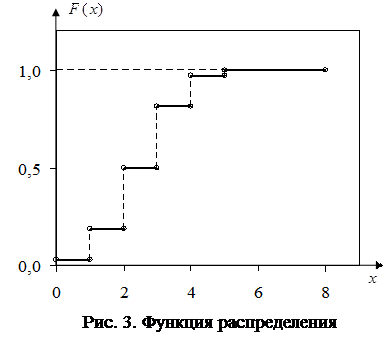
Найдем функцию распределения

x =0: Т.е. вероятность того, что величина X примет значение меньшее 0 равна нулю, поскольку слева от величины X= 0 нет ни единого возможного значения случайной величины. На графике ставим точку =(0;0).

x =1: Т.е. вероятность того, что величина X примет значение меньшее 1 равна вероятности того, что величина X примет значение равное нулю, поскольку слева от величины X= 1 есть единственное возможное значение X= 1. На графике ставим точку =(1;1/32) и проводим прямую =1/32 на участке, где .

x =2: Т.е. слева от величины X= 2 есть два возможных значения X= 0 и X= 1.

Аналогично:

Построим график этой функции.

Пример 2. Найти математическое ожидание дискретной слу­чайной величины X – числа таких бросаний пяти играль­ных костей, в каждом из которых на двух костях по­явится по одному очку, если общее число бросаний равно двадцати.

Решение: Имеем дело с биноминальным распределением. Здесь , а вероятность выпадения единицы на двух костях из пяти находим по формуле Бернулли: .

.

Пример 3. Дискретная случайная величина X имеет только два возможных значения: x ₁ и х ₂ , причем х ₂> х ₁. Вероятность того, что X примет значение х ₁равна 0,6. Найти закон распределения величины X, если математическое ожидание и дисперсия известны: М (Х)=1,4; D (X)=0,24.

Решение: Т.к. , то

.

Отсюда

.

Отсюда получаем уравнение:

Подставим сюда :

.

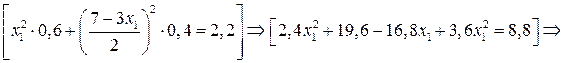
При .

 

При . Этот случай противоречит условию.

Значит закон распределения: .

 

Неравенство Чебышева

 

Вероятность того, что отклонение случайной величины Х от её среднего (математического ожидания) по абсолютной величине меньше положительного числа e, не меньше чем :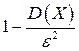

,

где D(X) – дисперсия дискретной случайной величины.

Другая форма неравенства:

.

Пример 4. Устройство состоит из 10 независимо работающих эле­ментов. Вероятность отказа каждого элемента за время Т равна 0,05. С помо­щью неравенства Чебышева оценить вероятность того, что абсолютная величи­на разности между числом отказавших элементов и средним числом (математи­ческим ожиданием) отказов за время Т окажется: а) меньше двух; б) не меньше двух.

Решение.

а) Обозначим через X дискретную случайную величину – число отка­завших элементов за время Т. Тогда

;

.

Воспользуемся неравенством Чебышева, подставив в него М(Х) = 0,5; D(X) = 0,475; e = 2, получим:

б) События 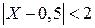и 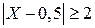противоположны, поэтому сумма их вероятностей равна единице. Следовательно,

.