Лекция 5
Непрерывные случайные величины
Первой производной от функции распределения F (x) является функция f (x), которая называется плотностью распределения вероятностей непрерывной случайной величины Х: 
Плотность распределения также называют дифференциальной функцией.
Случайная величина Х называется непрерывной, если ее функция распределения F (x) непрерывна на всей оси ОХ, а плотность распределения f (x) существует везде, за исключением, может быть, конечного числа точек.
Свойства функции распределения для дискретной случайной величины сохраняются и для непрерывной случайной величины.
Свойства дифференциальной функции распределения 
:
1. 
2. 
(условие нормировки),
3. 
Числовые характеристики непрерывных случайных величин
Математическое ожидание: 
.
Дисперсия: 
.
Среднее квадратичное отклонение: 
, и вероятность попадания случайной величины в интервал 
: 
Пример 1. Случайная величина задана плотностью распределения: 
Найти 
Решение: ● Константу 
найдем из условия нормировки: .
. Интегралы на участках 
и 
равны нулю, значит: 
● Найдем 
:
● Вычислим 
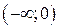не учитывая участки 
и 
.
● Вычислим вероятность попадания случайной величины в указанный интервал (0, 2): 
Равномерный закон распределения
Равномерным называют такое распределение вероятностей непрерывной случайной величины Х, при котором на интервале (a, b) плотность сохраняет постоянное значение, а именно 
; вне этого интервала 
.
Числовые характеристики равномерного закона:
; 
; 
; 
Пример 2. Автобусы некоторого маршрута идут строго по расписанию. Интервал движения 5 мин. Найти вероятность того, что пассажир, подошедший к остановке, будет ожидать очередной автобус менее 3 мин.
Решение: Интервал движения можно рассматривать как случайную величину Х, которая распределена равномерно в интервале между прибытием двух следующих друг за другом автобусов. Плотность равномерного распределения 
. Ожидание менее трех минут означает нахождение в интервале (0; 3). По формуле 
получим:
или иначе по формуле для равномерного закона: 
Экспоненциальный закон распределения
Экспоненциальным (показательным) называют распределение вероятностей случайной величины Х, которое описывается плотностью:
,
где 
– постоянная положительная величина.
Числовые характеристики экспоненциального закона распределения:
; 
; 
; 
.
Пример 3. Непрерывная случайная величина Х распределена по показательному закону, заданному плотностью вероятности 
при 
; 
при 
. Найти вероятность того, что в результате испытания Х попадает в интервал (0,13; 0,7).
Решение. Используем формулу:
Учитывая, что по условию a =0,13, b =0,7, 
, получим:
.
Нормальный закон распределения
Случайная величина 
называется распределенной по нормальному закону, если её плотность вероятности имеет вид:
где 
математическое ожидание, 
среднее квадратичное отклонение.
Нормальная кривая симметрична относительно прямой x = a.
Здесь 
, где 
функция Лапласа с аргументом 
.
Вероятность попадания случайной величины в интервал 
вычисляется как: 
Вероятность того, что абсолютная величина отклонения меньше положительного числа e: 
. Напомним, что F0(– z) =– F0(z).
Пример 4. Нормальная случайная величина X задана математическим ожиданием a =7 и средним квадратичным отклонением s =2. Вычислить вероятность попадания случайной величины X в интервал (6;8).
Решение: Из условия a =6; b =8.
Воспользуемся формулой и табл. прил.2:
.
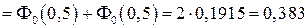Пример 5. Упаковка с вишневым соком заполняется автоматически. В среднем масса одной упаковки 1,1 кг. Найти среднее квадратическое отклонение, если 9% упаковок имеют массу меньше 1 кг. (предполагается, что массы упаковок распределены по нормальному закону).
Решение: Т.к. 9% имеют массу меньше 1 кг, то 91% упаковок имеют массу больше 1 кг. Это означает, что вероятность отклонения случайной величины от математического ожидания a =1,1 меньше положительного числа ε =0,1 равна 0,91:
.
По таблице прил.2 находим, что функция Лапласа равна 0,455 при значении аргумента z =1,70. Отсюда 
.