Основные типы распределения, используемые в лесном хозяйстве
Оглавление
Основные типы распределения, используемые в лесном хозяйстве. 1
1. Алгоритм определения закона распределения эмпирического ряда. 1
2. Нормальное распределение. 2
3. Логарифмически нормальное (логнормальное) распределение. 5
4. Распределение Вейбулла. 6
Алгоритм определения закона распределения эмпирического ряда
Случайная величина может быть задана в виде ряда распределения (численно или графически). На Рис.1 представлено распределение случайной величины в виде полигона частот. По данному графику наблюдаем определенные закономерности в распределении вариант: чем ближе значение вариант к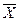 
, тем больше их частота, и наоборот, чем дальше, тем реже они встречаются.
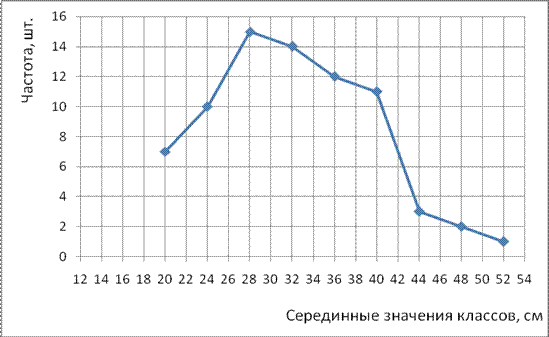
Рис. 1. Полигон частот
На практике теория распределения применяется в следующих направлениях:
· установление закона распределения исследуемой величины по выборке;
· получение аналитического вида распределения.
На Рис.2. представлен алгоритм установления закона распределения случайной величины.
 |
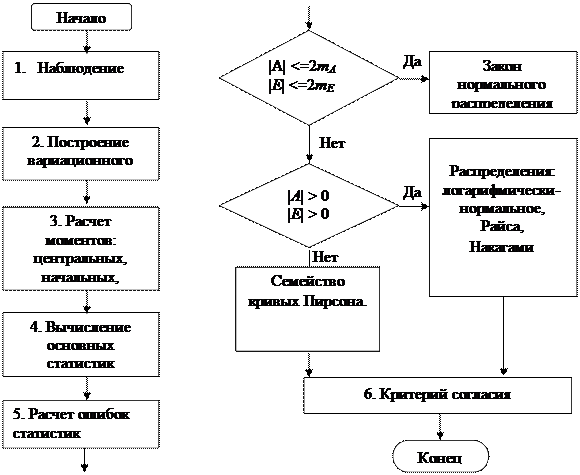Рис.2. Схема определения закона распределения
Существует более двух десятков различных законов распределения, в практике лесного хозяйства используют в основном следующие: нормальное, логарифмически нормальное, Пуассона и др.
Нормальное распределение
Тип непрерывного распределения, открыт А. Муавром в 1733 г (Англия), затем переоткрыт К. Гауссом (1809), П. Лапласом (1812), поэтому называется распределением Лапласа-Гаусса.
Распределение случайной величины считается нормальным, если коэффициенты асимметрии и эксцесса равны нулю. Это строгое условие, которое в природе наблюдается редко:
|
|
|
 |
(1)
Поэтому используют менее строгое условие, когда коэффициенты асимметрии и эксцесса не превышают своих двойных ошибок:
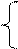
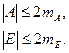(2)
Плотность нормального распределения ƒ(x) имеет вид:
ƒ(x)=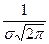 
exp 
; (3)
Функция распределения Ф(x) (функция накопленной вероятности)
Ф(x)=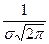 
dx, 
(4)
где 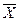– среднее значение,
– стандартное отклонение,
e – константа Эйлера, основание натуральных логарифмов, равное 2,718.
На графике (Рис.3) представлен график плотности нормального распределения ƒ(х) – это симметричная колоколообразная кривая. Форма ее зависит от величины , который является параметром масштаба, положение зависит от второго параметра – 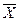. Т.е. нормальное распределение является двухпараметрическим распределением, параметрами которого являются: 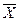и . Кривая имеет:
· один максимум ,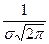
· две точки перегиба на расстоянии ±σ от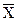 
.
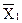
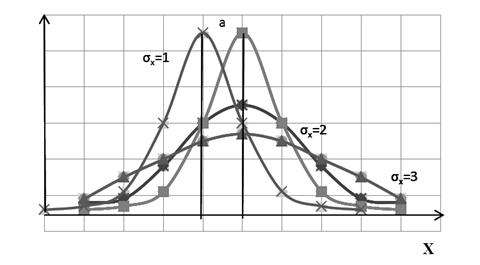
Рис.3. Кривая нормального распределения с различными параметрами
Вычисление плотности распределенияпо формуле (1) достаточно трудоемко. Поэтому составлены таблицы значений ƒ(x) и F(x) для стандартного распределения, где принято, что 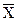=0 и σ =1. Также произведена замена переменных:
t=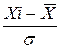 
(5)
тогда плотность и функция нормированного нормального распределения имеют вид:
ƒ(t)=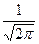 
exp(-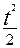 
) (6);
Ф(t)=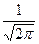 
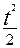(- )dt (7).
В Прилож. 3 приведены таблицы стандартного нормального распределения.
Свойства нормального распределения
1. Все варианты лежат в интервале 
, иными словами с вероятностью 1 (100%) ожидается появление новой варианты в пределах .
|
|
|
2. Слева и справа от средней арифметической лежит по 50% вариант, т.е., с вероятностью 0,5 (50%) можно предсказать появление новой варианты слева или справа от средней.
3. В интервале от 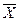±1 лежат 68,3% всех вариант, отсюда с вероятностью 0,683 (68,3%) можно прогнозировать появление новой варианты на расстоянии ±1 от средней – правило одной сигмы) (Рис.4, а);
4. Между 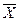±1,96 лежат 95% вариант. Это позволяет с 95%-ной вероятностью предположить, что новая варианта окажется в интервале 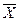±1,96 (округленно 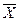±2 – правило двух сигм) (Рис.4, б);
5. С вероятностью 0,99 (99%) значение новой варианты будет заключено в пределах 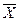±2,58 (правило трех сигм).) и с вероятностью 0,999 – в интервале 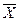±3,3 (Рис.4, в).
   
| а |
   
| б |
    
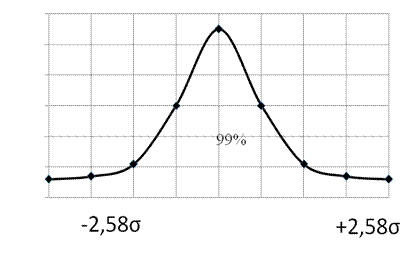
| в |
Рис. 4. Свойства кривой нормального распределения
Сравнение теоретических частот с эмпирическими с целью установить, отличается ли данное распределение от нормального, производят несколькими методами, например с использованием критерия Колмогорова-Смирнова, χ2-распределения.
