Задания к практической работе № 4

Задача 2.

Задание: Определить реакции опор балки на двух опорах. Схему выбрать в соответствии с номером студента по списку в журнале.

 

Принять: ;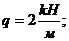

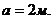
Порядок выполнения.

 

1. Изобразить схему в соответствии с вариантом.

2. Заменить распределенную нагрузку ее равнодействующей Q = q·l.

Приложить равнодействующую к балке в центре тяжести соответствующего прямоугольника.

3. Заменить опоры их реакциями. Реакцию шарнирно-подвижной опоры направить перпендикулярно к опорной поверхности.

 

Реакцию шарнирно-подвижной опоры разложить на две составляющие, направленные по осям координат.

 

4. Составить расчетную схему балки.

5. Выбрать оси координат и центры моментов.

6. Составить уравнение равновесия:

7. Из уравнений равновесия найти неизвестные реакции опор.

8. Провести проверку правильности решения, составив уравнения

9.Записать ответы.

10.Вывод.

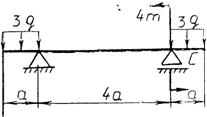
Задания к практической работе № 2

1	2	3
4	5	6
7	8	9
10	11	12

13

14

15

16	17	18
19	20	21
22	23	24

25	26	27
28	29	30

Тема 3. Определение координат центра тяжести плоской фигуры.

Задача 3.

Задание: Определить координаты центра тяжести сложной плоской фигуры. Схему выбрать в соответствии с номером студента по списку в журнале.

 

Порядок выполнения.

 

1. Изобразить заданную фигуру в соответствии с заданием в произвольном масштабе.

2. Выбрать оси координат.

3. Разбить фигуру на составные части, положение центров тяжести которых известно или легко определяется.

4. Определить площади составных частей. Площади вырезов принимать отрицательными.

5. Определять координаты центров тяжести составных частей.

6. Найденные значения площадей, а также координаты их центров тяжести представить в соответствующие формулы и вычислить координаты центра тяжести всей фигуры.

=

7. По найденным координатам нанести на эскизе положение центра тяжести фигуры.

8. Вывод.

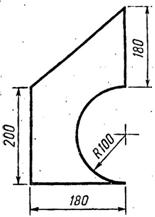
Задания к практической работе № 3

Вариант 1, 16	Вариант 2, 17	Вариант 3, 18	Вариант 4, 19	Вариант 5, 20
Вариант 6, 21	Вариант 7, 22	Вариант 8, 23	Вариант 9, 24	Вариант 10, 25
Вариант 11, 26	Вариант 12, 27	Вариант 13, 28	Вариант 14, 29	Вариант 15, 30

Тема 4. Расчеты стержней, испытывающих деформацию растяжения (сжатия).

Задача 4.

Задание: Для заданного двухступенчатого стального бруса, нагруженного двумя силами F₁ и F₂, построить эпюры продольных сил (N_z). Определить площади поперечных сечений и диаметр каждой ступени бруса из условия прочности; построить эпюры нормальных напряжений; определить удлинение (укорочение) каждой ступени и найти перемещение свободного конца бруса.

При расчетах принять =150МПа: Е=2·10⁵МПа. Исходные данные выбрать из таблицы.

Номер варианта взять в соответствии с номером студента в списках по журналу.

 

Порядок выполнения:

1. Изобразить расчетную схему в соответствии с вариантом.

2. Выписать исходные данные из таблицы.

3. Разделить брус на участки, границы которых определяются сечениями, где изменяются площадь поперечного сечения или приложены внешние нагрузки. Пронумеровать участки. Брус развернуть горизонтально.

4. Определить внутренние силовые факторы на каждом участке для чего применить метод сечения.

5. Построить эпюру N_z.

6. Из условия прочности при растяжении.

Найти площадь поперечных сечений бруса на каждом участке.

(мм²)

Определить диаметр каждого из сечений:

(мм)

Округлить диаметр до стандартного из ряда чисел R40.

Уточнить площади поперечных сечений:

8. Определить напряжения на каждом из участков.

(МПа)

9. Построить эпюру нормальных напряжений по длине бруса.

10. Определить деформацию каждого участка.

Δl_i= (мм)

11. Определить перемещение свободного конца бруса.

Δl=Δl₁+ Δl₂

12. Вывод.

Задания к практической работе № 4

Вариант 1, 11, 21	Вариант 2, 12, 22	Вариант 3, 13, 23	Вариант 4, 14, 24	Вариант 5, 15, 25
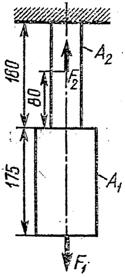
Вариант 6, 16, 26	Вариант 7, 17, 27	Вариант 8, 18, 28	Вариант 9, 19, 29	Вариант 10, 20, 30

Таблица данных для практической работы №4

вариант	1, 11,21	2,12,22	3, 13, 23	4,14, 24	5,15, 25	6,16, 26	7,17, 27	8, 18, 28	9, 19, 29	10, 20, 30
F1, кН
F2. кН