Обратимые и необратимые тепловые процессы
Тепловая машина. Цикл Карно. КПД цикла
В термодинамике наряду с первым началом, по существу выражающим закон сохранения энергии в тепловых процессах, фундаментальное значение имеет вопрос об их направленности. (Т.к. I – е начало т.д., устанавливающее связь между теплотой, изменением внутренней энергии и работой не определяет направление течения тепловых процессов).
В механике есть одно замечательное свойство движущихся тел, каково бы ни было механическое движение тела, всегда возможно обратноедвижение, при котором тело проходит те же точки пространства, с теми же скоростями, но в обратном направлении. Например, движение математического маятника.
Совершенно иная ситуация в области тепловых явлений – обратный процесс, происходящий по тем же состояниям, как правило невозможен.
Тепловые процессы, вообще говоря, являются необратимыми.
Примеры: 1) расширение газа в пустоту;
2) соприкосновение двух тел с различными температурами;
3) диффузия.
Обратимым будет процесс, отвечающий следующим условиям:
1) его одинаково легко провести в прямом и обратном
направлениях;
2) в каждом направлении тепловая система проходит через
одни и те же промежуточные состояния;
3) после проведения прямого и обратного процесса система
возвращается в исходное состояние.
Всякая предоставленная самой себе система тел стремится перейти в состояние теплового равновесия, в котором все тела покоятся друг относительно друга, во всех частях системы одно и то же давление и температура, не происходит изменений агрегатных состояний тел.
Любые процессы, сопровождающиеся трением, необратимы, но в некоторых случаях степень необратимости может быть столь незначительна, что процесс с определенной точностью можно считать обратимым. Для достижения этого нужно по возможности избегатьпроцессов, имеющих характер приближения к тепловому равновесию.
|
|
С помощью тел, находящихся в тепловом равновесии, невозможно произвести никакой работы, так как работа связана с механическим движением, т.е. с переходом внутренней энергии в кинетическую энергию движущихся тел.
Двигатель, работающий за счет тел, находящихся в тепловом равновесии – это вечный двигатель второго рода. Второй закон термодинамики устанавливает невозможность его построения. Таким образом, для получения работы нужна система тел, не находящаяся в тепловомравновесии. Если такая система будет состоять из двух тел, то скоро наступит термодинамическое равновесие и работы не будет. Следовательно, нужно 3 тела. Любая тепловая машина состоит из нагревателя, рабочего тела (газ) и холодильника. Схематично она изображается следующим образом:
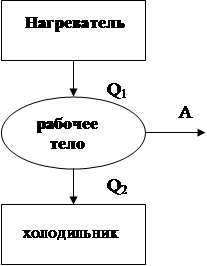
Большую роль в исследовании необратимости тепловых процессов сыграл французский инженер Сади Карно (в 1824 г.), причем задолго до установления закона сохранения энергии. (Осуществить практически такой цикл невозможно, т.к. приближение к циклу осуществимо лишь при очень медленном протекании процессов, что с технической точки зрения неприемлемо.Применяемые в технических тепловых машинах циклы необратимы и в действительности даже не замкнуты, т.к. в них рабочее вещество (пар, сгоревшая смесь) по окончании цикла выбрасывается наружу).
|
|
Рассмотрим равновесный циклический процесс, называемый циклом Карно. Это круговой процесс, состоящий из последовательно чередующихся двух равновесных изотермических и адиабатических переходов. Пусть тепловая машина совершает цикл Карно. В ходе цикла газ расширяется, получая от нагревателя теплоту Q1, затем сжимается, при этом передавая холодильнику теплоту Q2. Нагреватель имеет температуру Т1, а холодильник Т2, и в процессе работы тепловой машины они не изменяются.
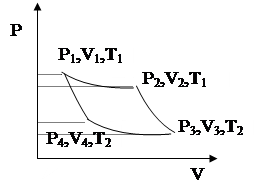
1) Прямой процесс начинается с изотермического расширения:
На этой стадии рабочее тело соединяют с нагревателем, процесс равновесный, температуры нагревателя и рабочего тела одинаковы и равны Т1. Рабочее тело получает от нагревателя количество теплоты Q1. Работа в изотермическом процессе:
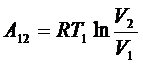, и 
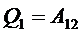
2) На этом этапе рабочее тело изолируют от нагревателя – температура его падает до T2, тепло не поступает, происходит адиабатическое расширение.
, 
.
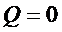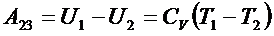3) Рабочее тело приходит в контакт с холодильником, отдавая ему количество теплоты Q2, происходит изотермическое сжатие при температуре T2.
,
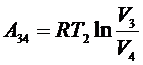причем A34 < 0 и – Q2 = A34
4) Рабочее тело изолируют от холодильника – происходит адиабатное сжатие до температуры T1 и объёма V1.
, 
.
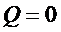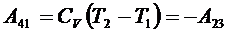Коэффициент полезного действия
.
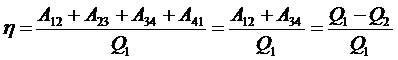Адиабатные участки не влияют на результат, так как работа на них равна и противоположна по знаку.
Максимальный КПД цикла можно определить через температуру:
.
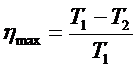Наиболее выгодным был бы тепловой двигатель с η = 1. В этом двигателе Q2 = 0, т.е. не требовалось бы наличие холодильника. Такая машина могла бы работать за счет охлаждения любых окружающих тел: внутренней энергии морей, океанов, воздушной атмосферы и недр Земли. Такую машину и назвали вечным двигателем II-го рода. Но, как сказано было выше, такую машину построить нельзя!
|
|
Энтропия
Происходит от слова «энтропос» – поворот, превращение в том смысле, что в природе различные виды энергии (мех-ие, эл-ие, световые, химические и др.) имеют тенденцию переходить в тепловую, т.е. в беспорядочное, хаотическое движение молекул. Собрать обратно эту энергию и превратить ее в те виды, из которых она была получена, оказывается невозможно.
Понятие энтропии введено Р. Клаузиусом.
Энтропия характеризует состояние системы так же, как внутренняя энергия, объём, давление, температура.
Функция, характеризующая направление протекания самопроизвольных процессов в замкнутой термодинамической системе, называется энтропией S:
dS =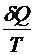 
, где
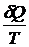– приведенная теплота.
Свойства энтропии:
1) Энтропия системы из нескольких тел является суммой энтропий каждого из них.
.
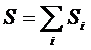2) В равновесных процессах без передачи тепла энтропия не меняется:
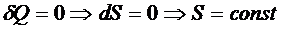
3) При постоянном объёме энтропия является монотонной функцией внутренней энергии
,
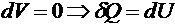так что
.
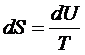4) Энтропия определяется с точностью до произвольной постоянной, поскольку измеряемой является только её разность в двух состояниях.
Необратимый характер процессов связан с переходом от состояний менее вероятных к состояниям более вероятным. Следовательно, энтропия, определяющая направление протекания необратимых процессов, должна быть связана с вероятностью. Больцман установил, что энтропия пропорциональна ln вероятности состояния:
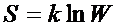, где
W – термодинамическая вероятность состояния системы, т.е. это число способов, которыми может быть реализовано данное состояние макроскопической системы (W ≥ 1).
Понятие энтропии определяет степень хаотичности системы, и чем больше энтропия, тем выше хаотичность. Поэтому, можно дать еще одно определение энтропии – это мера неупорядоченности (хаоса) системы.
Второе начало термодинамики
(закон возрастания энтропии)
Изменением энтропии (и только её) определяются свойства необратимости любых макроскопических процессов. Этот вывод называется вторым началом (законом) термодинамики. Он применим ко всем макроскопическим телам, за исключением Вселенной в целом. Современная его формулировка известна под названием закона возрастания энтропии и гласит, что: в каждой изолированной макроскопической системе изменение энтропии ΔS при любом реальном процессе удовлетворяет неравенству
Δ S≥ 0
При этом точность, с которой процесс является обратимым (равновесным)
Δ S = 0,
для необратимых неравновесных процессов
Δ S> 0.
Необратимые процессы приводят к установлению равновесного состояния. В этом состоянии энтропия изолированной системы достигаем максимума. Никакие макроскопические процессы в такой системе в дальнейшем невозможны.
Величина изменения энтропии является количественной характеристикой степени необратимости процесса.
К Вселенной в целом закон возрастания энтропии неприменим по причине того, что силы гравитации определяют свойства пространства и времени так, что по отношению к веществу Вселенной они выступают в качестве своеобразных внешних условий. И эти условия не стационарны, но изменяются. В этом смысле Вселенная не является изолированной системой, и, следовательно, закон возрастания энтропии неприменим.
Закон возрастания энтропии имеет два следствия, которые исторически были первыми формулировками второго начала термодинамики.
Первое из них – формулировка Р. Клаузиуса: