Данные коэффициенты применяются, когда представлена информация по альтернативным признакам, то есть тем, которые могут принимать только 2 значения (город-село, мужчины-женщины, согласен – не согласен и т.д.).
1. Нахождение частот: определяем долю избирателей, проживающих в городской и сельской местности, %.
2. Мода – величина, которая встречается чаще всего. В нашем случае, чаще всего, то есть проживает больше избирателей в городской местности.
3. Явка избирателей определяется отношением количество явившихся избирателей к числу избирателей в округе. В среднем по Удмуртии явка составила 56 %. Можно проследить связь: в сельской местности проживает меньше людей (избирателей), но их политическая активность выше (явка на выборы).
4. Определяем значимость – силу связи с помощью коэффициентов ассоциации и контингенции.
Таблица 4.4
Распределение избирателей УР по месту проживания по выборам
В Государственную Думу шестого созыва, 2011 год
| Показатель | республика | в том числе | |
| город | село | ||
| Число избирателей, чел. | |||
| Число избирателей, % | |||
| Число избирателей, явившихся на выборы, чел. | |||
| Число избирателей, явившихся на выборы, % | |||
| Доля явившихся из числа избирателей, % (ЯВКА) |
| a | b | a+b |
| c | d | c+d |
| a+c | b+d | a+b+c+d |
Коэффициент ассоциации: 
= 
Коэффициент контингенции: 
.
= 
Зависимость между явкой избирателей и местом проживания очень слабая, практически отсутствует.
Пример 4.6. Как Вы оцениваете состояние своего здоровья? Использование ранговой шкалы
Таблица 4.5
Результаты Европейского социального исследования 2014, доля, %
| Ранг | Германия | Дания | Эстония | Испания | Финляндия | Франция | Великобритания | Норвегия | Россия | |
| Очень хорошее | ||||||||||
| Хорошее | ||||||||||
| Среднее | ||||||||||
| Плохое | ||||||||||
| Очень плохое | ||||||||||
| Затрудняюсь ответить | ||||||||||
| Итого, % |
Используя ранги можно применить балльную оценку и определить итоговый результат с помощью средней арифметической взвешенной величины.
где, Хi – это балл за ответ;
fi – доля ответивших за указанный балл.
Согласно данным примера средняя оценка здоровья жителями Германии:
= 
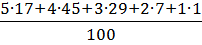= 3,67 баллов
Пример 4.7. Интервальная шкала населения, имеющего право голосовать на выборах, по возрасту, тыс. чел.
Таблица 4.6
Распределение населения Удмуртии по возрасту в 2011 и в 2015 гг.
| Исходная информация | Расчетные данные | ||||
| Возраст, лет | 2011 г. | 2015 г. | Х | 2011 г. Хifi | 2015 г. Хifi |
| 18-19 | 36,8 | 27,3 | 18,5 | 680,4 | 504,9 |
| 20-24 | 126,3 | 88,0 | 2778,3 | 1936,7 | |
| 25-29 | 128,2 | 128,0 | 3462,3 | 3457,3 | |
| 30-34 | 117,5 | 122,3 | 3761,3 | 3915,1 | |
| 35-39 | 106,9 | 112,6 | 3954,3 | 4167,6 |
Окончание табл. 4.6
| 40-44 | 94,6 | 100,8 | 3972,7 | 4235,4 | |
| 45-49 | 115,5 | 92,3 | 5428,2 | 4338,7 | |
| 50-54 | 131,5 | 118,0 | 6836,2 | 6133,7 | |
| 55-59 | 112,6 | 121,6 | 6418,8 | 6932,5 | |
| 60-64 | 80,0 | 99,2 | 4959,3 | 6149,8 | |
| 65-69 | 35,6 | 61,1 | 2383,3 | 4090,6 | |
| 70-74 | 56,6 | 33,9 | 4075,2 | 2442,0 | |
| 75-79 | 36,9 | 43,1 | 2841,4 | 3322,3 | |
| 80-84 | 26,0 | 25,1 | 2131,0 | 2057,0 | |
| 85 лет и старше | 11,5 | 16,2 | 996,2 | 1405,1 | |
| Итого | 1216,4 | 1189,6 | - | 54678,9 | 55088,6 |
Представлен интервальный ряд, ширина каждого интервала (за исключением первого) составляет 4 года.
Представим графически ряд распределения. По оси Х располагается возраст (лет), по оси У располагаем частоту (численность населения, чел.). Данный график называется полигон.
Рис. 4.1. Распределение населения Удмуртии по возрасту в 2011 и в 2015 гг.
Основной массив населения сосредоточен в возрасте от 18 до 65 лет.
Определим какой интервал по возрасту встречается чаще всего в каждом году, то есть Моду.
В 2011 г. модальным интервалом является возраст 50-54 года (численность или частота равна 131,5 тыс. чел).
В 2015 г. модальным интервалом является возраст 25-29 лет (частота 128,0 тыс. чел.).
Очевидно, что средний возраст в данном случае лучше определять с помощью средней аналитической величины – средней арифметической взвешенной (см. пример 4.6).
Для каждого интервала определяем конкретное – дискретное значение возраста – как середину интервала (крайние значение складывают и делят пополам), и заносим в таблицу.
Если интервал открыт (от 85 и старше), его величина берется равной ширине «соседнего» закрытого интервала.
Затем для каждого года определяем произведение возраста Х на численность (частоту) f, и заносим в таблицу.
Средний возраст населения, обладающего избирательными правами, составляет:
2011 год:
2015 год:
Таким образом, население избирательного возраста «постарело» более чем на 1 год, что подтверждает тенденцию старения населения России.