ТЕПЛОПРОВОДНОСТЬ ПРИ СТАЦИОНАРНОМ РЕЖИМЕ.
При установившемся, или стационарном тепловом режиме температура тела во времени остаётся постоянной, т. е. 
. При этом дифференциальное уравнение теплопроводности будет иметь вид:
или
. (1.2)
Если внутренние точки теплоты отсутствуют, то уравнение (1.2) упростится и примет вид:
или
.
Первым объектом рассмотрения является передача теплоты через плоскую стенку при 
.
При решении задач теплопроводности задаются граничными условиями первого рода. Рассмотрим однородную и изотропную стенку толщиной 
с постоянным коэффициентом теплопроводности 
. На наружных поверхностях стенки поддерживаются постоянные температуры 
и 
.
При заданных условиях температура будет изменяться только в направлении, перпендикулярном плоскости стенки. Если ось Оx направить, как показано на рисунке, то температура в направлении осей Oy и Oz будет оставаться постоянной, т.е. температурное поле будет одномерным:
.
В связи с этим температура будет функцией только одной координаты x и дифференциальное уравнение теплопроводности для рассматриваемого случая запишется в виде:
. (1.3)
Граничные условия (1-ого рода) при рассматриваемой задачи зададим следующим образом:
при 
(1.4)
при 
.
Дифференциальное уравнение (1.2) и граничные условия (1.4) дают полную математическую формулировку рассматриваемой задачи.
Цель задачи: найти распределение температуры в плоской стенке t=f(x) и формулу для определения количества теплоты.
Закон распределения температуры по толщине стенки можно найти путём двойного интегрирования уравнения (1.3):
первое интегрирование: 
второе интегрирование: 
(1.5)
Уравнение (1.5) -уравнение прямой линии. Отсюда следует, что при 
температура по толщине стенки изменяется по линейному закону.
Постоянные 
и 
можно определить из граничных условий первого рода (1.4):
при 
и 
;
при 
и 
.
Подставляя значения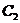 
и 
, получим закон распределения температуры в рассматриваемой плоскости стенке:
.
Для определения количества теплоты воспользуемся законом Фурье:
.
Получено, что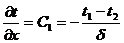 
.
После подстановки в закон Фурье получим:
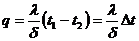. (1.6)
Количество теплоты, переданное через единицу поверхности стенки в единицу времени,прямо пропорционально коэффициенту теплопроводности и разности температур наружных поверхностей стенки и обратно пропорционально толщине стенки 
.
Следует отметить, что тепловой поток определяется не абсолютным значением температуры, а их разностью 
, называется температурным напором.
Отношение 
,[Вт/(
)], называется тепловой проводимостью стенки, а обратная величина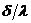 
, [ /Вт]- тепловым (термическим) сопротивление стенки.
Зная плотность теплового потока, можно вычислить количество теплоты 
, переданное через произвольную поверхность F за время 
:
.
Из уравнения (1.6) следует, что 
- введем это в уравнение температурного поля:
,
т.е. температура в стенке убывает тем быстрее, чем больше плотность теплового потока.
Если учесть зависимость от температуры, то получим более сложные формулы. Для подавляющего большинства материалов зависимость от t определяется уравнением:
.
После несложных преобразований можно видеть, что температура изменяется по кривой. Причём, если 
- положительно,товыпуклость кривой направлена вверх, если - отрицательно, то выпуклость кривой направлена вниз.