Показатели вариации
Размах вариации
Средняя величина дает обобщающую характеристику всей совокупности изучаемого явления. Однако два ряда распределения, имеющие одинаковую среднюю арифметическую величину, могут значительно отличаться друг от друга по степени колеблемости (вариации) величины изучаемого признака. Если индивидуальные значения признака ряда мало отличаются друг от друга, то средняя арифметическая будет достаточно показательной характеристикой данной совокупности. Если же ряд распределения характеризуется значительным рассеиванием индивидуальных значений признака, то средняя арифметическая будет ненадежной характеристикой этой совокупности и ее практическое применение будет ограничено.
Для измерения вариации признака применяются различные абсолютные и относительные показатели. К абсолютным показателям вариации относятся размах колебаний, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение и квартильное отклонение.
Вариацией значений какого-либо признака в совокупности называется различие его значений у разных единиц данной совокупности в один и тот же период или момент времени. Таким образом вариацией признака называется его изменение у единиц совокупности. Вариация порождается комплексом разнообразных условий, фактов, воздействующих на элементы совокупности. Изучение вариации имеет большое практическое и научное значение. Оно осуществляется при помощи показателей вариации.
Размах колебаний или размах вариации, представляет собой разность между максимальным и минимальным значениями признака в изучаемой совокупности:
R=Xmax-Xmin
где R – размах вариации,
Xmax – наибольшее значение признака,
Xmin – наименьшее значение признака.
Достоинством этого показателя является простота расчета. Однако размах вариации зависит от величины только крайних значений признака, поэтому область его применения ограничена достаточно однородными совокупностями. В частности, на практике он находит применение в предупредительном контроле качества продукции.
Дисперсия и среднее квадратическое отклонение
Дисперсия – средний квадрат отклонений индивидуальных значений признака от их средней величины.
Для несгруппированных данных:
, где
| σ²(сигма) | – дисперсия, |
| Хі | – значение признака отдельных единиц совокупности, |
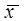
| – среднее значение всех единиц совокупности, |
| n | – численность совокупности. |
Для сгруппированных данных или вариационного ряда дисперсия вычисляется по следующей формуле:
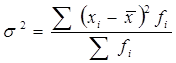, где
fі – численность групп.
Среднее квадратическое отклонение – представляет собой корень квадратный из дисперсии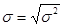 
, где s (сигма) – среднее квадратическое отклонение.
Размах вариации, среднее квадратическое отклонение являются именованными величинами. Чем меньше эти показатели, тем совокупность более однородна, тем более типичной будет средняя величина.