| Скорость движения, км/ч, не более | Уклон отвода возвышения наружного рельса, 0/00 | |
| рекомендуемый при реконструкции, капитальном ремонте на новых и старогодных материалах, усиленном среднем ремонте пути | Предельно допускаемый | |
| 0,5 | 0,5 | |
| 0,6 | 0,7 | |
| 0,6 | 0,7 | |
| 0,8 | 1,0 | |
| 0,9 | 1,2 | |
| 1,0 | 1,4 | |
| 1,6 | 1,9 | |
| 2,1 | 2,7 | |
| 2,7 | 3,1 | |
| 3,0 | 3,2 | |
| Движение закрывается | - | более 3,2 |
Примечания:
1. Уклон определяется на отрезках переходной кривой длиной не менее 30 м.
2. Допускаемые скорости также распространяются на отводы возвышения в пределах стрелочных съездов при расположении пути в разных уровнях.
По второму условию, ограничивающему скорость нарастания непогашенного горизонтального ускорения  , длина переходной кривой должна удовлетворять условию:
, длина переходной кривой должна удовлетворять условию:
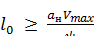 (2.8)
(2.8)
При  м/с2,
м/с2,  = 0,6 м/с3 и V в км/ч
= 0,6 м/с3 и V в км/ч
 (2.9)
(2.9)
Длину переходной кривой определяют по формуле
 (2.10)
(2.10)
и проверяют по условию (2.9).
Во всех случаях длина переходной кривой не должна быть менее 20 м. Полученные по расчету значения длины переходной кривой округляются до значения кратного 10 м в большую сторону.
Учитывая, что для конца переходной кривой l х = l() и  x = R, параметр переходной кривой определяется как:
x = R, параметр переходной кривой определяется как:
C = R· l0 (2.11)
Разбивка переходных кривых. Элементы переходных кривых, необходимые для их разбивки на местности, находятся в зависимости от способа разбивки. Различают следующие способы разбивки переходных кривых: способ сдвижки круговой кривой вовнутрь; способ введения дополнительных круговых кривых меньшего радиуса, чем радиус основной кривой; способ (Н.В. Харламова) смещения центра и изменение радиуса.
Рассмотрим случай разбивки переходных кривых способом сдвижки. Этот способ заключается в следующем. Для разбивки кривых по координатам необходимо знать сдвижку р круговой кривой и расстояние m 0 от НПК до тангенсного столбика Т0. Но для этого, прежде всего, находят т - расстояние от начала переходной кривой до нового положения тангенсного столбика Т, за тем определяют сдвижку р, угол  и все ординаты кривой.
и все ординаты кривой.
m = x0 – R sin  (2.12)
(2.12)
p = y0 – R(1-cos  ) = y0 – 2R sin2
) = y0 – 2R sin2  (2.13)
(2.13)
Тогда
m0 = m + ptg  (2.14)
(2.14)
Здесь х0 и у0 – координаты конца переходной кривой; угол касательной к кривой в той же точке с положительным направлением оси абсцисс равен  .
.
 (2.15)
(2.15)
Для переходной кривой

Во многих случаях значения m 0 и р находят приблизительно, имея в виду что кривизна переходной кривой изменяется пропорционально проекции ее длины  на ось х (в этом случае для разбивки принимают уравнения кубической параболы):
на ось х (в этом случае для разбивки принимают уравнения кубической параболы):




тогда
 ;
;  (2.17)
(2.17)
Возможность устройства переходных кривых длиной l 0 при угле поворота линии β определяется тем, чтобы длина круговой кривой была не меньше некоторого минимума Lmin:
R(β - 2  )
)  Lmin (2.18)
Lmin (2.18)
При этом Lmin определяется условием размещения в ее пределах полной колесной базы экипажа. Можно принять Lmin = 0, если алгебраическая разность уклонов отводов возвышения наружного рельса примыкающих друг к другу переходных кривых не будет превышать максимально допустимого (но не использованного) уклона отвода возвышения наружного рельса для каждой переходной кривой.
Проверяют возможность разбивки переходной кривой указанным способом по следующим условиям:
1. 
где β – заданный угол поворота кривой, рад.
2. Определяют длину круговой кривой Lкк:
Lкк = R( β - 2  ). (2.19)
). (2.19)
| где в- заданный угол поворота кривой, рад. 2. Определяют длину круговой кривой LKK: |
3. Сравнивают Lкк с минимально возможной длиной круговой кривой  , определяемой длиной полной базы расчетного экипажа, которая принимается не менее 30 м. Если это условие не выполняется, то следует изменить радиус кривой.
, определяемой длиной полной базы расчетного экипажа, которая принимается не менее 30 м. Если это условие не выполняется, то следует изменить радиус кривой.
Для осуществления разбивки переходной кривой необходимо определить ее вид.
Кубическую параболу применяют при условии
R  (2.20)
(2.20)
Координаты такой кривой определяют по формуле
yi =  (2.21)
(2.21)
Если условие (2.20) не выполняется, разбивка переходной кривой производится по радиоидальной спирали и координаты переходной кривой определяются по уравнениям:
 (2.22)
(2.22)
 (2.23)
(2.23)
Затем определяются основные размеры для разбивки переходной кривой: расстояния m по формуле (2.12) и т0 по формуле (2.14).
Полная длина новой кривой (с переходными кривыми):
Lкр = 2l0 + R( β - 2  ). (2.24)
). (2.24)
Суммарный тангенс новой кривой:
Ткр = m + (R+p)  . (2.25)
. (2.25)
Суммарная биссектриса:
Б = 
Разбивку переходных и круговых кривых на местности производят геодезическими способами.
| Полная длина новой кривой (с переходными кривыми): |
Суммированный тангенс новой кривой:
Суммированная биссектриса:
Пример 2.2 Требуется произвести расчет элементов переходной кривой для круговой кривой радиусом R = 500 м, находящейся на участке пути, подлежащем капитальному ремонту. При этом известны центральный угол поворота трассы β =22°30' и возвышение наружного рельса h = 130 м (пример 2.1).
1. Определяем длину переходной кривой по формуле (2.10)
l 0 = 
В соответствии с табл. 2.1 для Vmax n = 90 км/ч i=3‰. Тогда
l 0 =  = 100 м
= 100 м
Полученное значение l 0 округляется до величины, кратной 10 м, т.е. принимаем 0 = 110 м.
Этой переходной кривой при R = 500 м, будет соответствовать параметр
С = R·l0 = 500·110=55000 м2
Определим угол поворота  на протяжении переходной кривой по формуле (2.15)
на протяжении переходной кривой по формуле (2.15)
 рад.
рад.
 6018’
6018’
2. Проверим возможность разбивки переходной кривой по зависимостям
 и L кк = R (
и L кк = R ( )
)  30 м.
30 м.
Угол поворота трассы
 = 22030’ = 22,50
= 22030’ = 22,50  рад
рад
Длина круговой кривой
L кк = 500(0,3925 - 2·0,12 рад
Проверка выполняется:
 ; 0,3925 ˃ 2·0,12 рад
; 0,3925 ˃ 2·0,12 рад
L кк  30 м; 86,25 ˃ 30 м
30 м; 86,25 ˃ 30 м
Разбивка переходных кривых возможна.
3. Определим вид переходной кривой и координаты для ее разбивки в прямоугольной системе.
Для этой цели, прежде всего, проверим возможность применения в качестве переходной кривой кубической параболы из выражения (2.20)
R 
Найдем численное значение правой части этого выражения:
1,602· 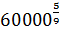 = 1,602·
= 1,602· 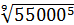 = 689 м.
= 689 м.
Условие (2.20) не выполняется (500<689м), и для разбивки переходной кривой принимаем радиоидальную спираль с определением координат по формулам (2.22) и (2.23) с расчетом их в табличной форме (табл. 2.2) и шагом i = 10 м.


По результатам расчетов таблицы 2.2 строится график переходной кривой в масштабе 1:100 (рис. 2.3).
Таблица 2.2
Координаты переходной кривой по радиоидальной спирали
|

|
Рис. 2.3. Координаты переходной кривой
4. Определяем элементы переходной кривой, которые необходимы для разбивки ее на местности.
Сдвижка круговой кривой внутрь определяется по формуле (2.14)
р = ук – R(1-cos  ) = 4,030 – 500(1-0,993956) = 1,008 м
) = 4,030 – 500(1-0,993956) = 1,008 м
Расстояние m от начала переходной кривой до отнесенного тангенсного столбика определим по выражению (2.12):
m = хк - Rsin  = 109,887 - 500·0,109778 = 54,998
= 109,887 - 500·0,109778 = 54,998
Расстояние т0 от начала переходной кривой до первоначального тангенсного столбика найдем по формуле (2.14):
m0 = m + ptgβ/2 = 54,998+1,008·0,198809=55,198 м
Полная длина новой кривой (с учетом переходных кривых) в соответствии с выражением (2.24):
L кр = 2 l0 + R (β-2  ) = 2·110+500(0,3925-2·0,11) = 306,25 м
) = 2·110+500(0,3925-2·0,11) = 306,25 м
Суммарный тангенс новой кривой определим по формуле (2.25):
Т кр = m +(R+p)tgβ/2 = 54,998+(500+1,008)·0,198809 = 154,603 м
Суммарная биссектриса определяется по формуле (2.26):
Б =  = 10,813 м
= 10,813 м
2.3. Расчет числа укороченных рельсов на внутренних нитях кривых.
В связи с тем, что в пределах кривых радиус внутренней рельсовой нити несколько меньше (на величину S0 = 1600 мм), радиуса наружной рельсовой нити, длина внутренней нити меньше наружной.
Для компенсации этой разницы и обеспечения укладки рельсовых нитей с положением стыков по одной нормали к продольной оси пути по внутренней нити кривой укладываются укороченные рельсы.
Полное укорочение на двух переходных кривых и круговой кривой будет равно:



где  - укорочение на переходной кривой;
- укорочение на переходной кривой;  .- укорочение на круговой кривой;
.- укорочение на круговой кривой;
So - расстояние между осями рельсов, равное 1600 мм;
R— радиус круговой кривой;
l 0 —длина переходной кривой;
L кк — длина круговой кривой.
Число укороченных рельсов, необходимых для укладки на внутренней нити кривой можно определить по формуле:
Ny =  (2.29)
(2.29)
Nнор=Nобщ-Ny
Nнор≥Ny
При этом следует сравнить число укороченных рельсов с числом нормальных рельсов Nh, которое можно уложить на всей длине кривой.
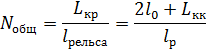
Где: l р- длинна рельса с учётом зазора (12,51м или 25,01м)
На дорогах в РФ приняты следующие типы укорочения Кi:
При длине рельса 12,5 м - К1 -40 мм, К2 - 80 мм и К3 - 120 мм(для бесстык. пути);
При длине рельса 25 м - К2 = 80 мм и К4 = 160 мм.
В курсовом проекте для выбора величины Ki следует руководствоваться длиной рельса и величиной радиуса кривой.
Минимальная величина стандартного укорочения К2 =80 мм принимается при радиусе кривой 500 м и более, а К4 = 160 мм радиусу кривой менее 500 м.
Ввиду невозможности обеспечить точное расположение «по наугольнику» стыков по внутренней и наружной нитям, допускается забег их на величину не более половины принятого укорочения. 
Рис 2.4 Схема радиусов рельсовых нитей в кривой
Пример 2.3
1. Определяем полное укорочение на двух переходных кривых и круговой кривой



. Число укороченных рельсов, необходимых для укладки на внутренней нити кривой можно определить по формуле (1.29) при Ki = 80 мм, т.к. R = 500 м.
Ny = 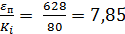 шт.
шт.
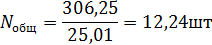
Nнор=12-8=4шт 4<8, т.е Nнор<Ny
Значит, величина укорочения для рельсов длинной 25,01м должна быть увеличена до 160мм
Тогда: 
Nнор=12-4=8шт, значит Nнор=8>Ny=4,требование выполняется.
Принимаем стандартное укорочение К=160мм. Расчётное количество укороченных рельсов в кривой R=500м равно: Ny=4шт из 12 рельсов на длине кривой 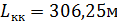 .
.
 , м
, м
 , м
, м