B-дерево
В-дерево – это сбалансированное многоходовое дерево. Особенностью В-дерева является то, что каждая вершина не должна содержать ровно N ключей; вершины В-дерева могут иметь свободное пространство, используемое для вставки новых элементов. Такая организация дерева упрощает операции вставки и удаления.
Название «В-дерево» можно объяснить двумя способами:
а) от слова Balanced – сбалансированное дерево, в котором все листья имеют один и тот же уровень;
б) от Bayer – автора данной структуры.
Введем определение В-дерева.
В-деревом порядка n называется структура, обладающая следующими свойствами:
1. Все пути от корня до любых листьев имеют одинаковую длину h, называемую также высотой В-дерева.
2. В каждой вершине дерева, за исключением корня, должно располагаться минимум n, максимум 2n ключей.
3. В корне В-дерева может располагаться минимум 1, максимум 2n ключей.
4. Любая вершина дерева, за исключением листьев, имеющая j ключей, должна иметь j+1 подчиненную вершину.
Последнее условие означает, что промежуточные вершины В-дерева имеют от n+1 до 2n+1 указателей на подчиненные вершины, а корень дерева – от 2 до 2n+1 указателей.
Таким образом, порядок В-дерева определяет степень его «пустоты» (или заполнения) – минимальное количество включенных в В-дерево элементов (или максимальное количество свободных позиций). Нижняя граница гарантирует, что вершины В-дерева заполнены, по крайней мере, наполовину. Верхняя граница позволяет определить регулярную структуру каждой вершины В-дерева.
Порядок дерева влияет на эффективность доступа: чем выше порядок дерева, тем ниже само дерево, а значит, тем меньше обращений к внешней памяти потребуется для поиска элемента.
Структура вершины В-дерева
Обозначим записи, размещенные в одной вершине дерева, через R1, R2, …, Rj, а указатели на подчиненные вершины через P0, P1, P2, …, Pj. Тогда структура вершины будет следующей:
P0 R1 P1 R2 P2 … Pj-1 Rj Pj
Правила следования:
1. Ключи записей в текущей вершине упорядочены по возрастанию, т.е. ключ записи R1 меньше ключа записи R2, который, в сою очередь, меньше ключа записи R3, и т.д.
1. Записи в подчиненной вершине, на которую указывает P0, имеют ключи, меньшие, чем ключ записи R1.
2. Записи в подчиненной вершине, на которую указывает Pj, имеют ключи, большие, чем ключ записи Rj.
Записи в подчиненной вершине, на которую указывает Pi (0 < i < j), имеют ключи, большие, чем ключ записи Ri, и меньшие, чем ключ записи Ri+1.
Ниже приведены примеры В-деревьев порядка 1 и порядка 2 (рис. II-53).

Рис. II-53.
Механизм поиска в В-дереве аналогичен механизму поиска в бинарном дереве и не требует дополнительных пояснений.
Операции включения и удаления должны:
- сохранять сбалансированность В-дерева и степень заполнения его вершин;
- не нарушать упорядоченности записей;
- свести к минимуму перемещение информации.
Операция вставки
Операции вставки предшествует поиск, который должен завершиться не успешно.
Следует иметь в виду (и это очень важно для понимания принципов использования В-дерева), что операция вставки позволяет включить новый элемент только в лист В-дерева. Поэтому, прежде всего, определяется целевая вершина – лист В-дерева, куда должен быть вставлен новый элемент, не нарушая упорядоченности записей.
Когда целевая вершина (лист) В-дерева будет найдена, можно столкнуться со следующими ситуациями.
1. Простейший случай, когда найденный лист имеет свободные позиции (не заполнен полностью). В этом случае новый элемент вставляется в найденный лист, не нарушая упорядоченности ключей.
Пусть, например, имеется следующий фрагмент В-дерева порядка 2 (рис. II-54, а; для удобства, на рисунке листья В-дерева пронумерованы). Необходимо вставить элемент с ключом 7. Новый элемент должен быть размещен в листе с номером 2, в котором есть свободные позиции. В результате выполнения операции вставки получим новое В-дерево (рис. II-54, б).

Рис. II-54.
2. Случай переполнения вершины: найденный целевой лист заполнен полностью. При вставке нового элемента в целевой лист получим последовательность из 2n+1 ключей, тогда как в листе могут находиться максимум 2n ключей. В этом случае выполняется операция расщепления листа: ключ из средней позиции переносится в родительскую вершину, а на уровне листьев появляются два новых листа.
Рассмотрим пример. Пусть в представленное выше дерево порядка 2 (рис. II-55, а) вставляется элемент с ключом 37. Поэтому получим последовательность ключей: 7, 10, 15, 23, 37. В средней позиции находится элемент с ключом 15; он перемещается в родительскую вершину, и появляются два новых листа (рис. II-55, б).

Рис. II-55.
Когда элемент перемещается в родительскую вершину, для нее также рассматриваются эти же две ситуации. Если родительская вершина заполнена полностью, для нее также выполняется операция расщепления с перемещением элемента на выше расположенный уровень. В результате высота дерева может увеличиться на 1.
Рассмотрим пример вставки нескольких значений в В-дерево порядка 1.
Пусть вставляется следующая последовательность элементов: 20, 12, 48, 3, 5, 70, 101.
1. Первые два элемента заполняют первый лист, который является одновременно и корнем В-дерева (рис. II-56).

Рис. II-56.
2. Вставляется следующий элемент – 48. Получаем переполнение: 12, 20, 48. Элемент из средней позиции поднимается вверх и создает новую вершину – корень В-дерева, которой подчинены два листа (рис. II-57).

Рис. II-57.
3. Элемент с ключом 3 вставляется в самый левый лист (рис. II-58).

Рис. II-58. Вставка элемента 3 в В-дерево
4. Элемент с ключом 5 также должен быть вставлен в самый левый лист; получаем переполнение – 3, 5, 12, и элемент из средней позиции перемещается в родительскую вершину, в которой есть свободное место (рис. II-59).
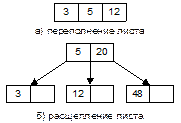
Рис. II-59.
5. Следующий элемент (70) вставляется в самый правый лист, в котором есть свободная позиция (рис. II-60).

Рис. II-60.
6. В тот же лист должен быть вставлен следующий элемент с ключом 101; получаем переполнение – 48, 70, 101, и элемент из средней позиции перемещается в родительскую вершину. В родительской вершине также возникает переполнение – 5, 20, 70; в результате перемещения элемента из средней позиции образуется новая вершина – корень В-дерева (рис. II-61), и высота дерева увеличивается на 1.

Рис. II-61.
Процесс вставок можно продолжать, включая в дерево новые элементы.
Таким образом, при вставке элементов в дерево В-дерево растет вверх – появляется новый корень, хотя новый элемент вставляется в лист дерева.
Удаление элемента
Ключ из В-дерева индексов удаляется из-за удаления записи из таблицы (из области данных). Операции удаления ключа предшествует успешный поиск вершины, в которой размещается удаляемый ключ.
Прежде всего, рассмотрим следующие две ситуации.
1. Искомый ключ находится в листе дерева. В этом случае операция удаления не затрагивает глобально структуру В-дерева.
2. Искомый ключ находится в промежуточной вершине. Удаление ключа не должно разрушить структуру В-дерева, поэтому в такой ситуации обычно используется один из двух (равноправных) подходов:
а) удаляемый ключ замещается элементом с минимальным значением ключа из правого поддерева, подчиненного удаляемому элементу;
б) удаляемый ключ замещается элементом с максимальным значением ключа из левого поддерева, подчиненного удаляемому элементу.
И в том, и в другом случае в итоге приходим к необходимости удалить элемент из листа дерева. Поэтому в дальнейшем будем рассматривать все примеры, удаляющие элементы из листьев дерева.
Конкретный алгоритм удаления должен использовать какой-то один из двух подходов. Будем использовать подход а).
При удалении элемента из листа также можно столкнуться с двумя ситуациями.
1. Простейшая ситуация, когда в листе находится более чем n элементов (n – порядок В-дерева). В этом случае удаление элемента не нарушает структуру В-дерева и заканчивается сразу же.
Рассмотрим пример. Пусть имеется следующий фрагмент В-дерева порядка 2 (рис. II-62).

Рис. II-62.
Пусть требуется удалить элемент с ключом 20. Удаляемый элемент находится в промежуточной вершине В-дерева. В правом поддереве, подчиненном удаляемому элементу, находим минимальный элемент – это 21, и перемещаем его на место удаляемого элемента. Поскольку лист был заполнен более чем наполовину, после перемещения элемента в нем осталось необходимое количество элементов. В итоге получим следующее состояние В-дерева (рис. II-63).

Рис. II-63.
2. Случай антипереполнения вершины: в целевом листе находится минимально допустимое количество элементов. При удалении элемента в листе остается недостаточное количество элементов – возникает антипереполнение, которое должно быть устранено.
Антипереполнение устраняется одним из двух способов: с помощью перераспределения элементов или с помощью сцепления вершин. Рассмотрим эти способы.
Перераспределение элементов
Рассматриваются соседние вершины дерева (слева или справа), подчиненные той же вершине и тому же ключу, что и целевая. Если хотя бы в одной из них имеется более n записей (где n – порядок В-дерева), выполняется перераспределение элементов.
Для этого объединяются оставшиеся элементы из целевой вершины (в количестве n – 1), выбранной соседней вершины (в количестве n + 1 + m, где m ³ 0) и их общий корень. В результате объединения будет получено (n – 1) + (n + 1 + m) + 1 = 2n + 1 + m вершин, где m ³ 0. Эти элементы перераспределяются между целевой и соседней вершинами так, что в каждой из них появится минимум n элементов, и один элемент поднимется в родительскую вершину. Отсюда видно, что операция перераспределения обратна операции расщепления, выполняемой при вставке элементов.
Рассмотрим пример. Пусть дан следующий фрагмент В-дерева порядка 3 (рис. II-64).

Рис. II-64.
Пусть удаляется элемент с ключом 276. В целевой вершине остается 2 элемента, что недостаточно.
В соседней вершине имеется 5 элементов, поэтому можно выполнить перераспределение элементов. В результате объединения получим 5 (левый лист) + 1 (родительская вершина) + 2 (целевой лист) = 8 элементов. Эти элементы могут быть перераспределены между вершинами, например, так, как показано на рис. II-65.

Рис. II-65.
В результате получена структура, удовлетворяющая определению В-дерева.
Сцепление вершин
Если в соседних слева и справа вершинах находится только минимально допустимое количество элементов, перераспределение использовано быть не может. В этом случае используется сцепление: вместо двух вершин, целевой и какой-либо соседней, создается одна, в которую помещаются элементы из двух вершин и их общего корня. В результате в новой вершине окажется 2n элементов – максимально возможное количество ключей в вершине В-дерева. Элемент из родительской вершины удаляется, а два указателя (левый и правый) для этого элемента объединяются в один, указывающий на вновь созданную вершину В-дерева.
Рассмотрим пример. Пусть дан следующий фрагмент В-дерева порядка 2 (рис. II-66).

Рис. II-66.
Удаляется элемент 15. В результате сцепления получим один лист и один указатель на него (рис. II-67).

Рис. II-67.
В результате такой операции сцепления количество элементов в родительской вершине уменьшается на единицу, и в ней также может возникнуть антипереполнение, которое разрешается одним из двух рассмотренных способов. В результате распространения антипереполнения высота В-дерева может уменьшиться на 1.
Рассмотрим пример. Пусть дано В-дерево порядка 1 (рис. II-68).

Рис. II-68.
Удаляется элемент 150. В соседней вершине только один элемент, поэтому выполняется сцепление. В результате возникло антипереполнение в родительской вершине (рис. II-69).

Рис. II-69.
Для данной вершины также выполняется сцепление, в результате которого в корне В-дерева не осталось ни одного элемента (рис. II-70). В такой ситуации пустая вершина – корень В-дерева удаляется, и высота дерева уменьшается на 1.

Рис. II-70.
Таким образом, можно указать следующие основные свойства В-дерева:
1. Ключи и ассоциированные с ними данные хранятся во всех вершинах В-дерева.
2. Поиск данных выполняется эффективно; максимальная длина пути равна высоте дерева, но может быть получена и меньшая длина пути, если искомый элемент расположен в какой-либо промежуточной вершине В-дерева.
3. Если требуется получить упорядоченный список всех значений, включенных в дерево (или, другими словами, выполнить последовательную выборку данных), должен использоваться алгоритм обхода дерева, который потребует многократное перемещение в одну и ту же вершину дерева.