Существование решения ОЗЛП и способы его нахождения.

План

Чтения лекции по учебной дисциплине

«Математические методы»

Раздел № 2. Линейное программирование.

Тема № 2.2. Основная задача линейного программирования.

Занятие №

Место проведения: аудитория.

Литература:

1. Венцель Е.С. Исследование операций. Задач, принципы, методология. – М.: Наука, 1980.

2. Шелобаев С.И. Математические методы и модели в экономике, финансах, бизнесе. – М.:ЮНИТИДАНА, 2001

Учебные вопросы и расчет времени

№п/п	Учебные вопросы	Время, мин	Методические указания
1. 2.	Основная задача ЛП (ОЗЛП). Существование решения.

1. Вводная часть. Организационный момент. План занятия. Основные требования.

2. Основная часть.

Основная задача ЛП (ОЗЛП).

Любую задачу линейного программирования можно свести к стандартной форме, так называемой «основной задаче линейного программирования» (ОЗЛП), которая формируется так: найти неотрицательные значения переменные x ₁, x ₂, …, x_n, которые удовлетворяли бы условиям – равенствам:

a ₁₁ x ₁ + a ₁₂ x ₂ + … + a _{1 n} x_n = b ₁,

a ₂₁ x ₁ + a ₂₂ x ₂ + … + a _{2 n} x_n = b ₂, (6.1.)

………………………………..

a_{m 1} x ₁ + a_{m 2} x ₂ + … + a_mn x_n = b_m.

и обращали бы в максимум линейную функцию этих переменных:

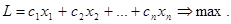(6.2.)

Случай, когда L надо обратить не в максимум, а в минимум, легко сводится к простому: изменить знак L на обратный (максимизировать не L, а L`=-L). Кроме того, от любых условий – неравенств можно перейти к условиям – равенствам ценой введения некоторых новых «дополнительных» переменных. Пусть требуется найти неотрицательные значения переменных x ₁, x ₂, x ₃, удовлетворяющие ограничениям – неравенствам

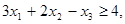(6.3.)

и обращающие в максимум линейную функцию от этих переменных:

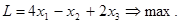(6.4.)

Начнём с того, что приведём условия (6.3.) к стандартной форме, так, чтобы знак неравенства был ³, а справа стоял нуль. Получим:

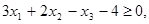(6.5.)

А теперь обозначим левые части неравенств (6.5.) соответственно через y ₁ и y ₂:

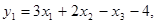(6.6.)

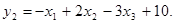
Из условий (6.5.) и (6.6.) видно, что новые переменные y ₁, y ₂ также должны быть неотрицательными.

Какая же теперь перед нами стоит задача? Найти неотрицательные значения переменных x ₁, x ₂, x ₃, y ₁, y ₂ такие, чтобы они удовлетворяли условиям – равенствам (6.6.) и обращали в максимум линейную функцию этих переменных (то, что в L не входит дополнительные переменные y ₁, y ₂, неважно: можно считать, что они входят, но с нулевыми коэффициентами). Перед нами – основная задача линейного программирования (ОЗЛП). Переход к ней от первоначальной задачи с ограничениями – неравенствами (6.3.) «куплен» ценой увеличения числа переменных на два (число неравенств).

Существование решения ОЗЛП и способы его нахождения.

Рассмотрим основную задачу линейного программирования (ОЗЛП): найти неотрицательные значения переменных x ₁, x ₂, …, x _n, удовлетворяющие m условиям – равенствам:

a ₁₁ x ₁+ a ₁₂ x ₂+…+ a _{1 n} x_n = b ₁,

a ₂₁ x ₁+ a ₂₂ x ₂+…+ a _{2 n} x_n = b ₂, (7.1.)

…………………………...

a_{m 1} x ₁+ a_{m 2} x ₂+…+ a_mn x_n =b _m

 

и обращающие в максимум линейную функцию этих переменных:

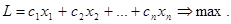(7.2.)

Для простоты предположим, что все условия (7.1.) линейно независимы (r = m), и будем вести рассуждения в этом предположении.

Назовём ДОПУСТИМЫМ решением ОЗЛП всякую совокупность неотрицательных значений x ₁, x ₂, …, x_n, удовлетворяющую условиям (7.1.).

ОПТИМАЛЬНЫМ назовём то из допустимых решений, которое обращает в максимум функцию (7.2.).

Требуется найти оптимальное решение. Всегда ли эта задача имеет решение? Нет, не всегда.

1. Может оказаться, что уравнения (7.1.) вообще несовместимы (противоречат друг другу).

2. Может оказаться и так, что они совместимы, но не в области неотрицательных решений, т.е. не существует ни одной совокупности чисел x ₁³0, x ₂³0, …, x_n ³0, удовлетворяющей условиям (7.1.).

3. Наконец, может быть и так, что допустимые решения ОЗЛП существуют, но среди них нет оптимального: функция L в области допустимых решений не ограничена сверху.

Чтобы представить себе принципиальную сторону ОЗЛП, обратимся к геометрической интерпретации. Пусть число уравнений m на два меньше числа переменных n (n - m = k =2). Такой частный случай даёт возможность геометрической интерпретации ОЗЛП на плоскости.

Мы знаем, что n линейно независимых уравнений (7.1.) всегда можно разрешить относительно каких-то m базисных переменных, выразив их через остальные, свободные, число которых равно n - m = k (в нашем случае k =2). Предположим, что свободные переменные – это x ₁ и x ₂ (если это не так, то всегда можно заново перенумеровать переменные), а остальные: x ₃, x ₄, …, x_n – базисные. Тогда вместо m уравнений (7.1.) мы получим тоже m уравнений, но записанных в другой форме, разрешённых относительно x ₃, x ₄, …;

x ₃= a ₃₁ x ₁+ a ₃₂ x ₂+ b ₃,

x ₄= a ₄₁ x ₁+ a ₄₂ x ₂+ b ₄, (7.3.)

……………………

x_n = a_{n 1} x ₁+ a_{n 2} x ₂+ b_n.

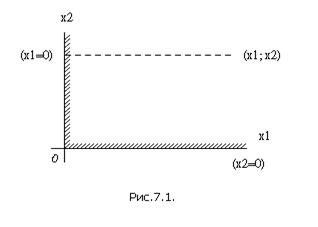
Будем изображать пару значений свободных переменных точкой с координатами x ₁, x ₂ (рис. 9.1.). Так как переменные x ₁, x ₂ должны быть неотрицательными, то допустимые значения свободных переменных лежат только выше оси Ox ₁ (на которой x ₂=0) и правее оси Ox ₂ (на которой x ₁=0). Это мы отметим штриховкой, обозначающей «допустимую» сторону каждой оси.

Теперь построим на плоскости x ₁ Ox ₂ область допустимых решений или же убедимся, что её не существует. Базисные переменные x ₃, x ₄, …, x_n тоже должны быть неотрицательными и удовлетворять уравнениям (7.3.). Каждое такое уравнение ограничивает область допустимых решений.

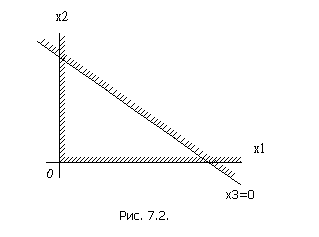
Действительно, положим в первом уравнении (7.3.) x ₃=0; получим уравнение прямой линии:

 

 

На этой прямой x ₃=0; по одну сторону от неё x ₃>0, по другую – x ₃<0. Отметим штриховкой ту сторону (полуплоскость), где x ₃>0 (рис. 7.2.). Пусть эта сторона оказалась правее и выше прямой x ₃=0. Значит, вся область допустимых решений (ОДР) лежит в первом координатном угле, правее и выше прямой x ₃=0. Аналогично поступим и со всеми остальными условиями (7.3.). Каждое из них изобразится прямой со штриховкой, указывающей «допустимую» полуплоскость, где только и может лежать решение (рис.7.3.).

 

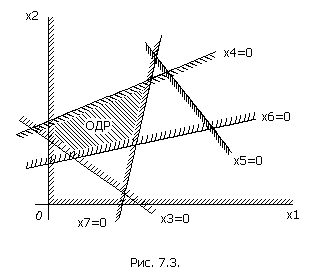
Таким образом, мы построили n прямых: две оси координат (Ox ₁ и Ox ₂) и n -2 прямых x ₃=0, x ₄=0, …, x_n =0. Каждая из них определяет «допустимую» полуплоскость, где может лежать решение. Часть первого координатного угла, принадлежащая одновременно всем этим полуплоскостям, и есть ОДР. На рис. 7.3. показан случай, когда ОДР существует, т.е. система уравнений (7.3.) имеет неотрицательные решения. Заметим, что этих решений – бесконечное множество, так как любая пара значений свободных переменных, взятая из ОДР, «годится», а из x ₁ и x ₂ могут быть определены и базисные переменные.

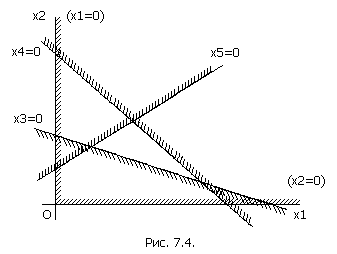
Может оказаться, что область допустимых решений не существует, и значит, уравнения (7.3.) несовместимы в области неотрицательных значений. Такой случай показан на рис. 7.4., где нет области, лежащей одновременно по «нужную» сторону от всех прямых. Значит, ОЗЛП не имеет решения.

Предположим, что область допустимых решений существует, и мы её построили. Как же теперь найти среди них оптимальное?

Для этого дадим геометрическую интерпретацию условию (7.2.) LÞmax. Подставив выражения (7.3.) в формулу (7.2.), выразим L через свободные переменные x ₁, x ₂. после приведения подобных членов получим:

 

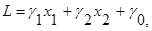(7.4.)

 

где ¡ ₁, ¡ ₂ – какие-то коэффициенты, ¡ ₀ – свободный член, которого в первоначальном виде у функции L не было; теперь, при переходе к переменным x ₁, x ₂, он мог и появится. Однако мы его тут же и отбросим: ведь максимум линейной функции L достигается при тех же значениях x ₁, x ₂, что и максимум однородной линейной функции (без свободного члена):

 

(7.5.)

 

Посмотрим, как изобразить геометрически условие L’Þmax. Положим сначала L’=0, т.е. 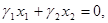и построим на плоскости x ₁ Ox ₂ прямую с таким уравнением; очевидно, она проходит через начало координат (рис. 7.5.)

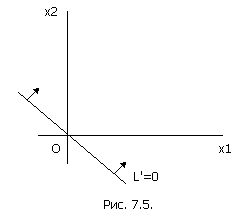
Назовём её «опорной прямой». Если мы будем придавать L’ какие-то значения C₁, C₂, C₃, …, прямая будет перемещаться параллельно самой себе; при перемещении в одну сторону L’ будет возрастать, в другую – убывать. Отметим на рис. 7.5. стрелками, поставленными у опорной рамой, то направление, в котором L’ возрастает. На рис. 7.5. это оказалось направление «направо - вверх», но могло быть и наоборот: всё зависит от коэффициентов g ₁, g ₂. теперь изобразим опорную прямую и ОДР на одном чертеже (7.6.). Давайте будем мысленно двигать опорную прямую параллельно самой себе в направлении стрелок (возрастания L’). Когда L’ достигнет максимума? Очевидно, в точке A (крайней точке ОДР в направлении стрелок). В этой точке свободные переменные принимают оптимальные значения x ₁^*, x ₂^*, а из них можно по формулам (7.3.) найти и оптимальные значения всех остальных (базисных) переменных x ₃^*, x ₄^*, …, x_n ^*. Заметим, что максимум L’ достигается в одной из вершин ОДР, где, по крайней мере, две из базисных переменных (в нашем случае это x ₃ и x ₅) обращаются в нуль. Могло бы обращаться в нуль и больше базисных переменных, если бы через точку А проходило более двух прямых x _i=0.

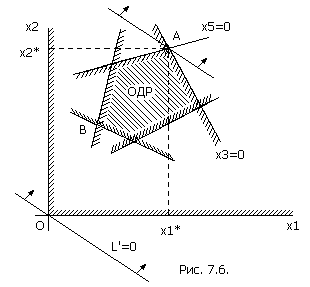
А может ли оказаться, что оптимального решения не существует? Да, может, если в ОДР функция L’ (а значит и L) не ограничена сверху. Пример такого ненормального случая показан на рис. 7.7. (в разумно поставленных задачах обычно такого недоразумения не возникает).

 

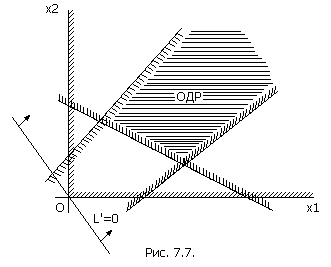
На рис. 7.6. оптимальное решение существовало и было единственным. А сейчас рассмотрим случай, когда оптимальное решение существует, но не единственно (их бесконечное множество). Это случай, когда максимум L’ достигается не в одной точке А, а на целом отрезке АВ, параллельном опорной прямой (рис. 7.8.).

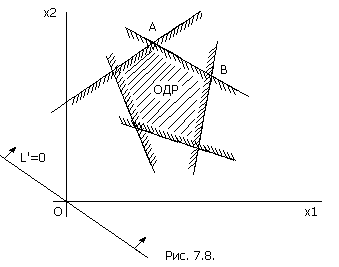
Итак, мы рассмотрели в геометрической интерпретации случай n - m = k =2 и убедились в следующем: оптимальное решение (если оно существует) всегда достигается в одной из переменных x ₁, x ₂, …, x_n равны нулю.

Оказывается, аналогичное правило справедливо и в случае n - m = k >2 (только геометрическая интерпретация теряет в этом случае свою наглядность). Обойдёмся без доказательства, просто сформулируем это правило.

Оптимальное решение ОЗЛП (если оно существует) достигается при такой совокупности значений переменных x ₁, x ₂, …, x_n, где, по крайней мере, k из них обращаются в нуль, а остальные неотрицательны.

При k =2 такая совокупность значений изображается точкой на плоскости, лежащей в одной из вершин многоугольника допустимых решений (ОДР). При k =3 ОДР представляет собой уже не многоугольник, а многогранник, и оптимальное решение достигается в одной из его вершин. При k >3 геометрическая интерпретация теряет наглядность, но всё же геометрическая терминология остаётся удобной. Мы будем продолжать говорить о «многограннике допустимых решений» в k -мерном пространстве, а оптимальное решение (если оно существует) будет достигаться водной из вершин этого многогранника, где, по крайней мере, k переменных равны нулю, а остальные – неотрицательны. Будем для краткости называть такую вершину «опорной точкой», а вытекающее из неё решение «опорным решением».

Отсюда вытекает идея, лежащая в основе большинства рабочих методов решения ОЗЛП, - идея «последовательных проб». Действительно, попробуем разрешить уравнения (7.1.) относительно каких–нибудь m базисных переменных и выразим их через остальные k свободных. Попробуем положить эти свободные переменные равными нулю – авось повезёт, наткнёмся на опорную точку. Вычислим базисные переменные при нулевых значениях свободных. Если все они оказались неотрицательными, значит, нам повезло, мы сразу же получим допустимое (опорное) решение, и его остаётся только оптимизировать. А если нет? Значит, данный выбор свободных и базисных переменных допустимого решения не даёт; точка лежит не на границе, а вне ОДР. Что делать? Надо «пере разрешить» уравнения относительно каких-то других базисных переменных, но не как попало, а так, чтобы это приближало нас к области допустимых решений (для этого в линейном программировании существуют специальные приёмы, на которых мы останавливаться не будем). Пусть, наконец, несколько раз повторив такую процедуру, мы нашли опорное решение ОЗЛП. Но это ещё не всё. Тут надо поставить вопрос: а является ли это решение оптимальным? Выразим функцию L через последние получившиеся свободные переменные и попробуем увеличить их сверх нуля. Если от этого значения L только уменьшается, значит, нам повезло, и мы нашли оптимальное решение, ОЗЛП решена. А если нет? Снова «пере разрешаем» систему уравнений относительно других базисных переменных, и снова не как попало, а так чтобы, не выходя за пределы допустимых решений, приблизиться к оптимальному. И опять- таки для этого в линейном программировании существуют специальные приёмы, гарантирующие, что при каждом новом «пере разрешении» мы будем приближаться к оптимальному решению, а не удаляться от него. На этих приёмах мы тоже здесь не будем останавливаться. После конечного числа таких шагов цель будет достигнута – оптимальное решение найдено. А если его не существует? Алгоритм решения ОЗЛП сам покажет вам, что решения нет.

Для простых задач, где число переменных невелико, такой «слепой перебор» может привести к решению, и довольно быстро. Но на практике часто встречаются задачи, в которых число переменных (и наложенных условий) очень велико, порядка сотен и даже тысяч. Для таких задач простой перебор становится практически невозможным: слишком велико число комбинаций свободных и базисных переменных. Пример: только при n =30 и m =10 число возможных комбинаций свободных переменных с базисными равно, т.е. свыше 30 миллионов! А эта задача – далеко не из сложных.

Разработанные в теории линейного программирования вычислительные методы («симплекс-метод», «двойственный симплекс-метод» и другие) позволяют находить оптимальное решение не «слепым» перебором, а «целенаправленным», с постоянным приближением к решению. Добавим, что совместимые ЭВМ, как правило, снабжены подпрограммами для решения задач линейного программирования, так что лицу, желающему их решить, нет даже особой надобности обучаться решению таких задач «вручную» - труд крайне неприятный и изнурительный.