Практическое занятие № 99

Контрольная работа № 8 по теме: «Многогранники и круглые тела»

1. Тело, ограниченное конической поверхностью и кругом с границей L, называется...

a) Сферой;

b) Цилиндром;

c) Параллелепипедом;

d) Конусом.

1. Основанием прямого параллелепипеда является ромб с диагоналями 6 см и 3 см, а высота параллелепипеда равна 8 см. Найдите большую диагональ параллелепипеда

a)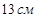

b)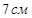

c)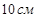

d)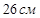

1. Какая фигура получится в осевом сечении конуса, у которого радиус основания конуса равен половине образующей?

a) Равносторонний треугольник;

b) Равнобедренный треугольник;

c) Окружность;

d) Прямоугольник.

1. Какая фигура получится в сечении цилиндра, если секущая плоскость параллельна плоскостям оснований?

a) Прямоугольник;

b) Треугольник;

c) Круг;

d) Пятиугольник.

1. Найдите площадь боковой поверхности прямой треугольной призмы, если одна из сторон основания равна 5 см, а высота составляет 3см?

a)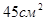

b)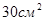

c)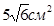

d)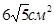

1. Какая фигура получиться в сечении конуса, которое параллельно плоскости основания?

a) Круг, радиус которого больше радиуса основания конуса;

b) Круг, радиус которого меньше радиуса основания конуса;

c) Круг, радиус которого равен радиусу основания конуса;

d) Равнобедренный треугольник.

1. Площадь боковой поверхности цилиндра вычисляется по формуле

a)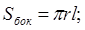

b)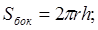

c) 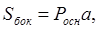где 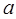- апофема.

1. В правильной треугольной призме сторона основания равна 3 см и высота 5 см. Вычислить площадь боковой поверхности призмы.

a)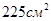

b)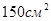

c)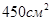

d)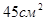

1. Призма – это...

a) Многогранник, составленный из двух равных многоугольников, расположенных в параллельных плоскостях, и 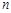параллелограммов;

b) Правильный многогранник, составленный из двадцати равносторонних треугольников;

c) Многогранник, составленный из 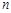-угольника и 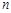треугольников.

1. Боковой гранью правильной шестиугольной усечённой пирамиды является...

a) Треугольник;

b) Равнобедренный треугольник;

c) Равнобедренная трапеция;

d) Прямоугольник.

1. Что представляет собой сечение конуса плоскостью, проходящей через его вершину и параллельное его основанию?

a) Круг;

b) Отрезок;

c) Точка;

d) Равнобедренный треугольник.

1. Найдите диагональ осевого сечения, если радиус цилиндра равен 2 м, а высота 3 м.

a)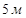

b)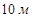

c)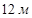

d)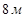

1. Какая из перечисленных фигур не является сечением конуса

a) Точка;

b) Круг;

c) Трапеция;

d) Треугольник.

1. Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, будем называть...

a) Плоскостью;

b) Многогранником;

c) Гранью многогранника;

d) Двугранным углом.

1. Площадь боковой поверхности правильной пирамиды равна

a) Произведению периметра основания на высоту призмы;

b) Сумме оснований призмы умноженных на высоту призмы;

c) Половине произведения периметра основания на апофему;

d) Произведению половины длины окружности основания на образующую.

1. Цилиндр может получиться путем вращения

a) Прямоугольника;

b) Треугольника;

c) Трапеции;

d) Пятиугольника

1. Какое наименьшее число ребер может иметь многогранник?

a) 5

b) 6

c) 8

d) 9

1. Площадь боковой поверхности прямой призмы равна...

a) Произведению периметра основания на высоту призмы;

b) Сумме оснований призмы умноженных на высоту призмы;

c) Половине произведения периметра основания на апофему;

d) Произведению половины длины окружности основания на образующую.

 

Критерии оценивания:

4, 5,16 задания оцениваются 2-мя балами, остальные по 1 баллу

11 – 14 баллов – «3» 15 – 18 баллов - «4» 19 – 21 балл - «5»

Баллы снижаются за отсутствие рисунка к задаче и отсутствие решения задачи. В определениях решений быть не может.