Лекция
Тема: Предел функции
План лекции:
1. Предел Числовая последовательность и ее предел
2. Предел функции на бесконечности и в точке
3. Основные теоремы о пределах
4 Замечательные пределы
Предел числовой последовательности
Если по некоторому закону каждому числу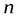 
поставлено в соответствие вполне определенное число 
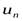, то говорят, что задана числовая последовательность 
:
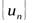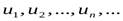(4.1)
Числа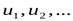 
называются членами ряда, а член 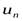общим или 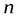-м членом ряда. Числовая последовательность называется заданной, если известен ее общий член 
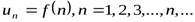, т.е. задана функция 
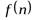натурального аргумента.
Существуют числовые последовательности, как с конечным числом членов, так и с бесконечным.
В случае бесконечной числовой последовательности мы сможем определить вид любого ее члена, зная функциональную зависимость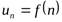 
.
Последовательность называется:
1. ограниченной сверху, если все члены ее меньше одного и того же числа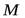 
:
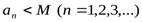(4.2)
2. ограниченной снизу, если все члены ее больше одного и того же числа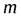 
:
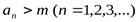(4.3)
3. ограниченной, если она ограничена и сверху и снизу:
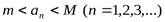(4.4)
Приведем пример нескольких бесконечных числовых последовательностей:
2, 4, 6, …, 2 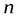, … (монотонная неограниченная)
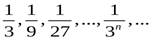(монотонная ограниченная)
1, 0, 1, 0, 1, … (немонотонная ограниченная)
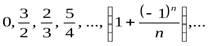(немонотонная ограниченная)
Всякая конечная последовательность, очевидно, ограничена. В качестве 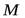можно взять любое число, большее, чем наибольший из членов последовательности; в качестве 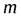– любое число, меньшее, чем наименьшее из членов последовательности.
Совсем по иному обстоит дело с бесконечными последовательностями. В данном случае возможны следующие варианты: числовая последовательность ограничена сверху, числовая последовательность ограничена снизу, также они могут быть неограниченными ни сверху, ни снизу.
Числовая последовательность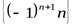 
является неограниченной, ни сверху, ни снизу.
Всякая точка, обладающая тем свойством, что в любой ее окрестности содержится бесконечное множество членов последовательности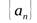 
, называется предельной точкой этой последовательности.
Используя данный термин, можно сформулировать теорему Больцано-Вейерштрасса:
Всякая ограниченная бесконечная последовательность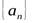 
имеет, по крайней мере, одну предельную точку.
Заметим, что различные последовательности могут иметь то или иное количество предельных точек; существуют также последовательности, которые обладают бесконечным множеством предельных точек (например, последовательность из всех рациональных чисел, занумерованных произвольным образом). При этом предельная точка может как «принадлежать» данной числовой последовательности, т.е. входить в состав ее членов, так и не принадлежать ей.
.Если ограниченная последовательность имеет одну предельную точку, то эта точка называется пределом числовой последовательности.
Если же ограниченная последовательность имеет более одной предельной точки, то говорят, что последовательность не имеет предела.
Последовательность
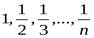(4.5)
Последовательность имеет одну предельную точку 0 (рис. 4.1).
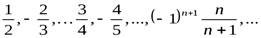
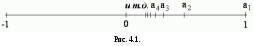
(4.6)
имеет две предельной точки -1 и 1 (рис.4.2).
Таким образом, из двух приведенных выше числовых последовательностей первая из них имеет предел, а вторая нет.
Приведем теперь классическое определение предела.
Постоянное число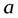 
называется пределом последовательности 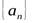, если для любого сколь угодно малого положительного числа 
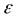существует номер 
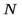, что все значения 
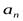, у которых 
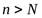, удовлетворяют неравенству:
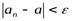(4.7)
Для обозначения того факта, что 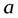– есть предел последовательности 
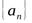, применяется следующая запись:
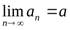(4.8)
Последовательность, имеющая предел, называется сходящейся, в противном случае – расходящейся.
Геометрический смысл понятия предела числовой последовательности состоит в следующем. Число 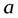– есть предел числовой последовательности, 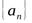, если для любого 
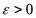найдется номер 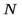, начиная с которого (при 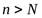) все члены последовательности будут заключены в 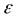– окрестности точки 
.
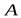Предел функции
Понятие предела функции является обобщением понятия предела числовой последовательности, так как предел последовательности можно рассматривать как предел функции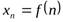 
целочисленного аргумента .
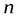Рассмотрим следующую функцию:
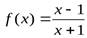(4.9)
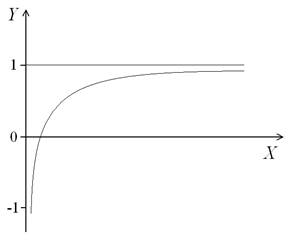Рис. 4.4.
Если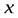 
принимает только целые значения, то значения этой функции будут вести себя также как и последовательность.
При стремлении к бесконечности x значение функции будет все ближе и ближе подходить к единице, что видно из графика на рис.4.4. Это пример недостижимого предела.
Функция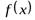 
стремится к пределу 
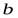при 
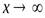, если для каждого произвольного сколь угодно малого положительного числа 
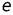можно указать такое положительное число N что для всех значений 
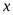, удовлетворяющих неравенству 
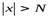будет выполняться неравенство:
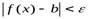(4.10)
Этот предел функции обозначается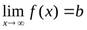 
или 
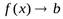при .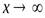
Смысл определения состоит в том, что при достаточно больших по модулю значениях x значения функции f(x) как угодно мало отличаются от числа b (по абсолютной величине).
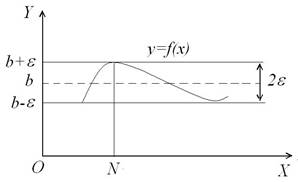Рис. 4.5.
Геометрически число 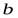есть предел функции 
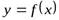при 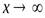, если для любого 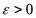найдется такое число 
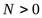, что для всех 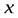, таких, что 
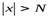, соответствующие ординаты графика функции 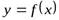будут заключаться в полосе 
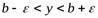, какой бы ни была эта полоса (рис.4.5).
Приведенное выше определение предела функции при 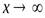предполагает неограниченное возрастание переменной 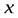по абсолютной величине. В то же время можно сформулировать понятие предела при стремление к бесконечности определенного знака, т.е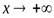. при 
и при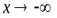 
. В первом случае неравенство (4.10) должно выполняться для всех x таких, что 
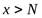, а во втором – для всех 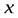таких, что 
.
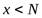Число a называется пределом функци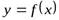и при 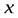стремящемся к 
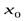(или в точке 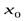), если для любого, даже сколь угодно малого, числа 
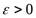, найдется такое число 
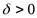(зависящее от , 
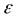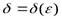), что для всех 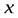, не равных 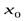и удовлетворяющих условию
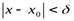(4.11)
выполняется неравенство:
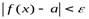(4.12)
Это определение называют определением предела функции по Коши. Смысл определения предела функции 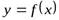в точке 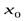состоит в том, что для всех значений 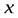достаточно близких к 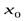, значения функции 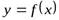как угодно мало отличаются от числа 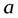(по абсолютной величине).