Работа №2 Системы эконометрических уравнений
Пример решения типовой задачи
Изучается модель вида

где  – расходы на потребление в период
– расходы на потребление в период 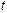 ,
,  – совокупный доход в период
– совокупный доход в период  ,
,  – инвестиции в период
– инвестиции в период  ,
,  – процентная ставка в период
– процентная ставка в период  ,
,  – денежная масса в период
– денежная масса в период  ,
,  – государственные расходы в период
– государственные расходы в период  ,
,  – расходы на потребление в период
– расходы на потребление в период  ,
,  инвестиции в период
инвестиции в период  .
.
Первое уравнение – функция потребления, второе уравнение – функция инвестиций, третье уравнение – функция денежного рынка, четвертое уравнение – тождество дохода.
Модель представляет собой систему одновременных уравнений. Проверим каждое ее уравнение на идентификацию.
Модель включает четыре эндогенные переменные  и четыре предопределенные переменные (две экзогенные переменные –
и четыре предопределенные переменные (две экзогенные переменные –  и
и  и две лаговые переменные –
и две лаговые переменные – 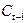 и
и  ).
).
Проверим необходимое условие идентификации для каждого из уравнений модели.
Первое уравнение:  . Это уравнение содержит две эндогенные переменные
. Это уравнение содержит две эндогенные переменные  и
и  и одну предопределенную переменную
и одну предопределенную переменную 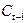 . Таким образом,
. Таким образом,  , а
, а  , т.е. выполняется условие
, т.е. выполняется условие  . Уравнение сверхидентифицируемо.
. Уравнение сверхидентифицируемо.
Второе уравнение:  . Оно включает две эндогенные переменные
. Оно включает две эндогенные переменные  и
и  и одну экзогенную переменную
и одну экзогенную переменную  . Выполняется условие
. Выполняется условие  . Уравнение сверхидентифицируемо.
. Уравнение сверхидентифицируемо.
Третье уравнение:  . Оно включает две эндогенные переменные
. Оно включает две эндогенные переменные  и
и 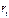 и одну экзогенную переменную
и одну экзогенную переменную  . Выполняется условие
. Выполняется условие  . Уравнение сверхидентифицируемо.
. Уравнение сверхидентифицируемо.
Четвертое уравнение:  . Оно представляет собой тождество, параметры которого известны. Необходимости в идентификации нет.
. Оно представляет собой тождество, параметры которого известны. Необходимости в идентификации нет.
Проверим для каждого уравнения достаточное условие идентификации. Для этого составим матрицу коэффициентов при переменных модели.

| 
| 
| 
| 
| 
| 
| 
| |
| I уравнение | –1 | 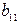
| 
| |||||
| II уравнение | –1 | 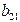
| 
| |||||
| III уравнение | –1 | 
| 
| |||||
| Тождество | –1 |
В соответствии с достаточным условием идентификации ранг матрицы коэффициентов при переменных, не входящих в исследуемое уравнение, должен быть равен числу эндогенных переменных модели без одного.
Первое уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

| 
| 
| 
| 
| |
| II уравнение | –1 | 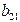
| 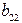
| ||
| III уравнение | –1 | 
| |||
| Тождество |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы  не равен нулю:
не равен нулю:
 .
.
Достаточное условие идентификации для данного уравнения выполняется.
Второе уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

| 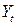
| 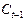
| 
| 
| |
| I уравнение | –1 | 
| 
| ||
| III уравнение | 
| 
| |||
| Тождество | –1 |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы  не равен нулю:
не равен нулю:
 .
.
Достаточное условие идентификации для данного уравнения выполняется.
Третье уравнение. Матрица коэффициентов при переменных, не входящих в уравнение, имеет вид

| 
| 
| 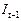
| 
| |
| I уравнение | –1 | 
| |||
| II уравнение | –1 | 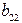
| |||
| Тождество |
Ранг данной матрицы равен трем, так как определитель квадратной подматрицы  не равен нулю:
не равен нулю:
 .
.
Достаточное условие идентификации для данного уравнения выполняется.
Таким образом, все уравнения модели сверхидентифицируемы. Приведенная форма модели в общем виде будет выглядеть следующим образом:

Задание на практическую работу
1 часть. Выполняется по индивидуальным вариантам
1. Даны системы эконометрических уравнений.
Требуется
1. Применив необходимое и достаточное условие идентификации, определите, идентифицируемо ли каждое из уравнений модели.
2. Определите метод оценки параметров модели.
3. Запишите в общем виде приведенную форму модели.
Вариант 1
Модель протекционизма Сальватора (упрощенная версия):

где
 – доля импорта в ВВП;
– доля импорта в ВВП;
 – общее число прошений об освобождении от таможенных пошлин;
– общее число прошений об освобождении от таможенных пошлин;
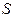 – число удовлетворенных прошений об освобождении от таможенных пошлин;
– число удовлетворенных прошений об освобождении от таможенных пошлин;
 – фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет;
– фиктивная переменная, равная 1 для тех лет, в которые курс доллара на международных валютных рынках был искусственно завышен, и 0 – для всех остальных лет;
 – реальный ВВП;
– реальный ВВП;
 – реальный объем чистого экспорта;
– реальный объем чистого экспорта;
 – текущий период;
– текущий период;
 – предыдущий период.
– предыдущий период.
Вариант 2
Макроэкономическая модель (упрощенная версия модели Клейна):

| где
 – потребление; – потребление;
 – инвестиции; – инвестиции;
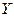 – доход; – доход;
 – налоги; – налоги;
 – запас капитала; – запас капитала;
 – текущий период; – текущий период;
 – предыдущий период. – предыдущий период.
|
Вариант 3
Макроэкономическая модель экономики США (одна из версий):

| где
 – потребление; – потребление;
 – ВВП; – ВВП;
 – инвестиции; – инвестиции;
 – процентная ставка; – процентная ставка;
 – денежная масса; – денежная масса;
 – государственные расходы; – государственные расходы;
 – текущий период; – текущий период;
 – предыдущий период. – предыдущий период.
|
Вариант 4
Модель Кейнса (одна из версий):
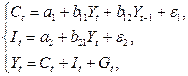
| где
 – потребление; – потребление;
 – ВВП; – ВВП;
 – валовые инвестиции; – валовые инвестиции;
 – государственные расходы; – государственные расходы;
 – текущий период; – текущий период;
 – предыдущий период. – предыдущий период.
|
Вариант 5
Модель денежного и товарного рынков:
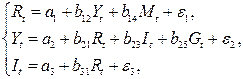
| где
 – процентные ставки; – процентные ставки;
 – реальный ВВП; – реальный ВВП;
 – денежная масса; – денежная масса;
 – внутренние инвестиции; – внутренние инвестиции;
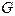 – реальные государственные расходы. – реальные государственные расходы.
|
Вариант 6
Модифицированная модель Кейнса:

| где
 – потребление; – потребление;
 – доход; – доход;
 – инвестиции; – инвестиции;
 – государственные расходы; – государственные расходы;
 – текущий период; – текущий период;
 – предыдущий период. – предыдущий период.
|
Вариант 7
Макроэкономическая модель:

| где
 – расходы на потребление; – расходы на потребление;
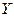 – чистый национальный продукт; – чистый национальный продукт;
 – чистый национальный доход; – чистый национальный доход;
 – инвестиции; – инвестиции;
 – косвенные налоги; – косвенные налоги;
 – государственные расходы; – государственные расходы;
 – текущий период; – текущий период;
 – предыдущий период. – предыдущий период.
|
Вариант 8
Гипотетическая модель экономики:

| где
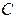 – совокупное потребление в период – совокупное потребление в период  ; ;
 – совокупный доход в период – совокупный доход в период  ; ;
 – инвестиции в период – инвестиции в период  ; ;
 – налоги в период – налоги в период  ; ;
 – государственные доходы в период – государственные доходы в период  . .
|
Вариант 9
Модель Менгеса:

| где Y - национальный доход; C - расходы на личное потребление; I - чистые инвестиции; Q - валовая прибыль экономики; P - индекс стоимости жизни; R - объем продукции промышленности. |
Вариант 10
Модель мультипликатора-акселератора:

где C – расходы на потребление, R - доход, I - инвестиции, t - текущий период, t-1 – предыдущий период.
Вариант 11
Конъюнктурная модель имеет вид:

где C – расходы на потребление, Y – ВВП, I – инвестиции, r – процентная ставка, M – денежная масса, G – государственные расходы, t – текущий период, t-1 – предыдущий период.
Вариант 12
Для прогнозирования спроса на свою продукцию предприятие использует следующую модель, характеризующую общую экономическую ситуацию в регионе:

где Q – реализованная продукция в период t, Y – ВДС региона, C – конечное потребление, I – инвестиции, K – запас капитала, t – текущий период, t-1 – предыдущий период.
Вариант 13
Дана следующая структурная форма модели:

где 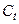 -- личное потребление в период t,
-- личное потребление в период t,  - зарплата в период t,
- зарплата в период t,  -- прибыль в период t,
-- прибыль в период t,  -- общий доход в период t,
-- общий доход в период t,  -- общих доход в период t-1, t-1 – предыдущий период.
-- общих доход в период t-1, t-1 – предыдущий период.
Вариант 14
Имеется модель кейнсианского типа:

где C – совокупное потребление в период t, Y – совокупный доход в период t, I – инвестиции в период времени t, T – налоги в период времени t, G – государственные расходы в период времени t, Yt-1 – совокупный доход в период t-1.
Вариант 15
Модель спроса и предложения на деньги:

где R – процентные ставки в период t, Y – ВВП в период t, M – денежная масса в период t, t – текущий период, t-1 – предыдущий период.
Вариант 16
Модель денежного рынка:

где R – процентные ставки, Y – ВВП, M – денежная масса, I – внутренние инвестиции, t – текущий период, t-1 – предыдущий период.
Вариант 17
Рассматривается следующая модель:

где  -- заработная плата в период t,
-- заработная плата в период t,  -- чистый национальный доход в период t,
-- чистый национальный доход в период t,  - денежная масса в период t,
- денежная масса в период t, 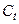 - расходы на потребление в период t,
- расходы на потребление в период t,  -- расходы на потребление в период t-1,
-- расходы на потребление в период t-1,  -- уровень безработицы в период t,
-- уровень безработицы в период t,  -- уровень безработицы в предыдущий период,
-- уровень безработицы в предыдущий период,  - инвестиции в период t, t - текущий период,
- инвестиции в период t, t - текущий период,  t-1 – предыдущий период.
t-1 – предыдущий период.
Часть.
1. Дана модифицированная модель Кейнса:

где
 – потребление;
– потребление;  – доход;
– доход;  – инвестиции;
– инвестиции;  – государственные расходы;
– государственные расходы;
 – текущий период;
– текущий период; 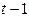 – предыдущий период.
– предыдущий период.
| годы | ||||||||||||||||||||
| Y | 95,75 | 98,55 | 103,55 | 108,25 | 107,4 | 112,7 | 117,75 | 123,45 | 126,55 | 125,85 | 128,1 | 125,35 | 130,25 | 138,3 | 142,65 | 146,80 | 151,3 | 157,4 | 161,25 | |
| C | 60,45 | 62,45 | 65,9 | 68,9 | 68,45 | 73,55 | 76,55 | 79,7 | 81,6 | 81,55 | 82,55 | 83,45 | 87,35 | 91,55 | 95,50 | 101,75 | 105,4 | 107,45 | ||
| I | 14,3 | 15,85 | 17,75 | 19,7 | 18,1 | 14,6 | 17,35 | 22,15 | 22,3 | 19,8 | 25,25 | 24,85 | 24,5 | 25,8 | 26,15 |
а) В предположении, что потребление зависит линейно от дохода (первое уравнение модели), оцените по МНК параметры  и
и  функции потребления.
функции потребления.
б) Оцените те же параметры по ДМНК
в) Сравните полученные результаты. Сделайте выводы по качеству оценок.