ЛекцИя 4. экстраполяция по трендовым моделям
4.1. Виды трендовых моделей
4.2. Оценка параметров трендовых моделей.
4.3. Измерение тесноты и направления святи при прогнозировании
4.1.
В прогнозировании используются два основных класса моделей: временных рядов и каузальные. Для построения модели временного ряда не требуется знания ни производства, ни даже экономических условий, в которых происходит процесс. Модель строится исключительно на основе имеющейся числовой информации. Задача прогнозиста при этом заключается в том, чтобы понять статистическую закономерность, которой подчиняются числа, образующие временной ряд, и сделать прогноз на будущее, основываясь на этой закономерности.
Каузальные модели в отличие от моделей временных рядов требуют глубокого знания производства, области и макроэкономической ситуации. Модели временных рядов в некоторых случаях дают не худшие, а даже лучшие результаты по сравнению с каузальными моделями.
Объяснение этому удивительному факту находят в том, что числовая информация, представляющая некоторый экономический или бизнес-процесс, уже содержит в себе, хотя и в неявном виде, будущие экономические или другие изменения и закономерности.
Временной ряд можно разложить (процесс декомпозиции) на 3 компонента:
1) Тренд f(уt) — некоторая аналитическая функция, которая связывает единым ‘‘законом движения’’ все последовательные уровни временного ряда. Тренд описывает общую тенденцию на базе лишь одного фактора – фактора времени (t). Следовательно не полностью описывает характер тенденции развития и не может рассматриваться как закон развития явления.
Временной ряд — это числовые последовательности образования уровней во времени (только в одном направлении);
Временной ряд экономических показателей как правило содержит долговременную или краткосрочную тенденции развития, связанные с преодолением случайных колебаний;
Временные ряды могут быть подвержены регулярным колебаниям, связанным с сезонностью, ритмичностью и другими периодическими колебаниями.
2) сезонные колебания (колебания в течении одного года - St или циклическая компонента (колебания в течении нескольких лет) - С t
3) случайная компонента - e
Аналитически все компоненты можно выразить уравнением вида:
 ,
,
где f(t) — некоторая функция времени, описывающая тенденцию исходного временного ряда, называемая
трендом;
Уровни временного ряда не всегда являются составляющими всех трех компонентов одновременно. Единственным компонентом, который встречается во временных рядах является случайный компонент, который может быть представлен в сочетании с определенной тенденцией или с какими-то периодическими колебаниями.

 y
y
- исходный временной ряд



- тренд





Рис.1. Пример процесса декомпозиции временного ряда
Для отображения основной тенденции развития явлений во времени или модели этого процесса применяются разные уравнения, полиномы разной степени, экспоненты, логистические кривые и другие функции.
Подобрать кривую (или набор кривых), заданную уравнением, которая бы приблизительно описывала тренд в исходной информации, т. е. общую тенденцию в изменении данных – основная задача прогнозиста.
Аналитическое выравнивание временного ряда состоит из следующих этапов:
1) выбор типа кривой, форма которой соответствует характеру изменения временного ряда;
2) определение численных значений (оценивание) параметров кривой.
В прогнозировании оцененное значение переменной принято обозначать с крышечкой наверху: ŷ.
Полиномы имеют следующий вид:
полином первой степени  ,
,
полином второй степени  , (1)
, (1)
полином n-й степени  .
.
Наиболее простым путем решения проблемы выбора формы трендовой модели можно назвать графический, на базе общей конфигурации графика фактических уровней ряда. Однако при этом подходе риск ошибочного выбора кривой очень велик. Правильность выбора уравнения в некоторой мере зависит от масштаба графика. Однако в несложных случаях подход графического выбора может дать вполне приемлемые результаты.
Подбор класса выравнивающих кривых для временного ряда производится на основе качественного анализа представленного им процесса, а также если известны:
D1,D2,D3…….Di – первые, вторые, третьи и т.д. разности или абсолютные ускорения;
TpD¢ - темпы роста первых абсолютных приростов уровней;
Тр – темпы роста.
В этих случаях критерии выбора типа кривой следующие (табл.1).
Таблица 1
Критерии выбора класса, выравнивающих кривых
| Показатель | Изменение уровней временного ряда | Формула уравнения | Наименование функции |
| D¢ D¢¢ | более или менее постоянные ≈0 | `yt=a0+a1t | линейная |
| D¢ | уменьшающиеся | `yt=a0+a1/t | гиперболическая |
| D¢ | изменяющиеся с насыщением | `yt=k/(1+be-at) | логистическая |
| D¢¢ | постоянны | `yt=a0+a1t+ a2t2 | параболическая 2-ой степени |
| D¢¢¢ | постоянны | `yt=a0+a1t+ a2t2+ a3t3 | параболическая 3-ой степени |
| D¢¢¢¢ | постоянны | `yt=a0+a1t+ a2t2+ a3t3+ a4t4 | параболическая 4-ой степени |
| TpD1 | постоянны | `yt= a0×a1t (`yt=aet) | экспоненциальная |
Парабола: ŷ t=a0+a1t+ a2t2

Рисунок 1. Кривая подгонки — парабола
У равнение логарифмической функции имеет вид: ŷ = а 1 + а 2ln(t)
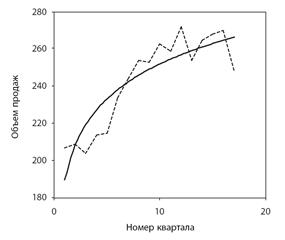
Рисунок 2. Кривая подгонки — график логарифмической функции
Экспоненциальная кривая ŷ = a0×a1t

Рисунок 3. Кривая подгонки — экспоненциальная кривая
Степенная функция ŷ = а 1(t)а2
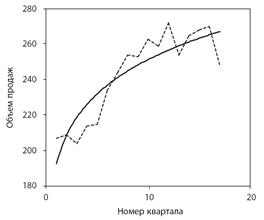
Рисунок 4. Кривая подгонки — график степенной функции
Гипербола: ŷ = a0+a1/t

Рисунок 5. Кривая подгонки — гипербола
Найденная модель позволяет получить выровненные или, как иногда называют, теоретические значения уровней, которые наблюдались бы при совпадении динамики явления с кривой найденной модели.
4.2.