Информационно-образовательные технологии

Новоуральский технологический институт

 

 

УТВЕРЖДАЮ

Зам. руководителя

 

____________ Г.С. Зиновьев

 

"_____"________ 20___ г.

 

Рабочая программа

учебной дисциплины " Математика "

(Первый – четвёртый семестры)

 

Направление подготовки	–	38.03.02 «Менеджмент»
Профиль	–	«Менеджмент»
Квалификация (степень) выпускника	–	академический бакалавр
Форма обучения	–	заочная

 

г. Новоуральск, 2014

МиМ 2.3- -14

 

Объем учебных занятий в часах:

 

Семестр					всего
Трудоемкость, ЗЕТ
Трудоемкость, ч.
Аудиторные занятия, в т.ч.:
- лекции
- практические занятия
-лабор. работа
Самостоятельная работа
Контроль
Форма итогового контроля	Зачёт	Зачёт	Экзамен	Экзамен	2З, 2Э

 

Индекс дисциплины

в Рабочем учебном плане (РУП) – Б1.Б.6.

 

Учебную программу составил ст. преподаватель кафедры высшей математики НТИ НИЯУ МИФИ Орлов Юрий Владимирович

 

Учебная программа рассмотрена на заседании кафедры Высшей математики НТИ НИЯУ МИФИ

 

"______"________________ 20 ___ г. протокол № _________

и рекомендована для подготовки бакалавров.

 

Заведующий кафедрой высшей математики

 

Н.А. Носырев ________________ «____» _______ 20____ г.

 

СОДЕРЖАНИЕ

	Цели освоения учебной дисциплины…………………….
	Место учебной дисциплины в структуре ООП ВО ……..
	Планируемые результаты обучения по учебной дисциплине и их соотношение с планируемыми результатами освоения образовательной программы.......
	Структура и содержание учебной дисциплины
	4.1.1 Семестр 1 ……………………………………………..
	4.1.2 Семестр 2...…………………………………………...
	4.1.3 Семестр 3...…………………………………………...
	4.1.4 Семестр 4...…………………………………………...
	Информационно-образовательные технологии………....
	Оценочные средства для текущего контроля успеваемости и учебно-методическое обеспечение самостоятельной работы студентов ……………………..
	Учебно-методическое и информационное обеспечение учебной дисциплины ……………………………………..
	Материально-техническое обеспечение учебной дисциплины ………………………………………………...

 

Рабочая программа составлена в соответствии с Образовательным стандартом высшего образования Национального исследовательского ядерного университета «МИФИ» по направлению подготовки 38.03.02 «Менеджмент» (квалификация (степень) «академический бакалавр»), утвержденный ученым советом университета и рабочим учебным планом (РУП) по направлению подготовки 38.03.02 «Менеджмент» профиль «Менеджмент».

Цели освоения учебной дисциплины

Целью освоения учебной дисциплины "Математика" является воспитание достаточно высокой математической культуры, развитие у студентов широкого кругозора в области математики и умения использовать математические методы и основы математического моделирования для решения практических задач.

 

Место учебной дисциплины в структуре образовательной программы

В соответствии с кредитно-модульной системой подготовки бакалавров по направлению 38.03.02 «Менеджмент» учебная дисциплина «Математика» входит в базовую часть основного раздела общепрофессионального модуля.

Дисциплина содержит разделы Линейная алгебра и аналитическая геометрия, Математический анализ, Ряды, Дифференциальные уравнения и их системы, Вероятность, Математическая статистика.

Предшествующий уровень образования обучаемого – среднее (полное) общее образование либо среднее профессиональное образование.

Изучение данной дисциплины базируется на сумме знаний и практических навыков, полученных студентами в среднем образовании на предметах Алгебра и Геометрия. Изучается дисциплина в первых четырёх семестрах (двух первых курсов).

Методы, развиваемые в данном курсе, являются базовыми при изучении других компонентов цикла и многих спецпредметов, они применяются при решении большинства прикладных задачах.

 

3. планируемыЕ результатЫобучения по учебной дисциплине И ИХ соотнОШЕНИЕ с планируемыми результатами освоения образовательной программы

Данный раздел устанавливает сквозное соотношение между планируемым результатом (ПР) в данной учебной дисциплине (УД) и образовательной программе (ОП).

 

Планируемые результаты освоения образовательной программы, относящиеся к учебной дисциплине

В результате освоения содержания дисциплины «Математика» студент должен обладать следующими компетенциями (Таблица 1)

 

Таблица 1 Компетенции, реализуемые при изучении дисциплины

 

Код компетенции	Компетенции
Профессиональные компетенции
ПК-8	владением навыками количественного и качественного анализа информации при принятии управленческих решений, построения экономических, финансовых и организационно-управленческих моделей путем их адаптации к конкретным задачам управления

Данную компетенцию реализуют дисциплины:

Б1.Б.6 Математика

Б1.Б.7 Статистика: теория статистики, социально-

экономическая статистика

Б1.Б.8 Методы принятия управленческих решений

Б1.Б.16 Учет и анализ: финансовый анализ

Б1.Б.17 Финансовый менеджмент

Б1.В.ДВ.3.1 Системный анализ

Б1.В.ДВ.3.2 Эконометрика

Б1.В.ДВ.5.1 Разработка управленческих решений

Б1.В.ДВ.9.2 Экономическая оценка инвестиций

Б1.В.ДВ.10.1 Логистика

Б2.П.2 Преддипломная практика

ИГА Итоговая государственная аттестация

 

Планируемые результаты обучения по учебной дисциплине

В результате освоения дисциплины «Математика» студент должен:

Знать:

З1 – основные понятия векторной и линейной алгебры;

З2 – основы аналитической геометрии;

З3 – основные понятия дифференциального и интегрального исчисления;

З4 – критерии сходимости числовых и функциональных рядов;

З5 – основные понятия дифференциальных уравнений и их систем;

З6 – определение и методы вычисления вероятностей;

З7– распределения и числовые характеристики случайных величин;

З8 – основные методы математической статистики и корреляции.

 

Уметь:

У1 - применять математические методы векторной и линейной алгебры;

У2 – применять математические методы аналитической геометрии;

У3 - применять дифференциальное и интегральное исчисления;

У4 - применять теорию рядов и дифференциальных уравнений при решении инженерных задач;

У5 – находить вероятности случайных событий;

У6 – составлять распределения случайных величин и находить их числовые характеристики;

У7 – выполнять обработку одномерных и двумерных статистических данных.

 

Владеть:

В1 – различными методами решения систем линейных уравнений;

В2 – методами решения типовых задач по темам: линии на плоскости, линии и поверхности в пространстве;

В3 – методами исследования функций и построения их графиков;

В4 – методами решения типовых задач геометрии и физики на основе интегрального исчисления;

В5 – методами исследования сходимости числовых и функциональных рядов;

В6 – методами решения обыкновенных дифференциальных уравнений I и II порядка и линейных систем ДУ;

В7 – действиями с случайными событиями и навыками вычисления их вероятностей;

В8 – методами обработки статистических данных.

3.3. Соотношение планируемых результатов обучения по учебной дисциплине и результатов освоения образовательной программы

Таблица 2

Планируемый результат освоения образовательной программы, относящиеся к учебной дисциплине (ПР ОП)	Планируемый результат обучения по учебной дисциплине (ПР УД)	Соотношение
ПК-8	З1–З8, У1–У7, В1–В8	Б1.Б.6/ПК-8/З1– Б1.Б.6/ПК-8/В6

 

4. Структура и содержание учебной дисциплины

Общий объем дисциплины при заочной форме обучения (ЗФО) 17 ЗЕТ, 612 ч..

4.1. Структура учебной дисциплины. Соотношение лекций, практических занятий, лабораторных занятий, с их распределением по учебным неделям семестра, трудоёмкостью в часах, самостоятельной работой и методам контроля по каждому из семестров рассмотрено в п. 4.1.1 – 4.1.4.

4.1.1 Семестр – 1 Трудоёмкость 8 ЗЕТ, 288 ч., зачёт

Таблица 3

№ п/п	Название темы/раздела учебной дисциплины	Неделя семестра	Виды учебных занятий, и их трудоемкость (в часах)	Ссылка на ПР УД	Форма контроля
Лекции	Практические занятия	Лабораторные занятия	Самостоятельная работа
1.	Матрицы, определители	1-2					З1, У1, В1	Дз-1 Часть 1
2.	Решение линейных систем	3-4
3.	Линейные действия над векторами	5-6
4.	Скалярное, векторное, смешанное произведение векторов	7-8
5.	Прямая на плоскости	9-10					З1-З2, У1-У2, В1-В2	Дз-1 Часть 2
6.	Плоскость и прямая в пространстве	11-12
7.	Кривые второго порядка	13-14
8.	Поверхности второго порядка	15-16
	Итого:
9.	Зачёт (З-1)

Дз-1 «Задания по математике, 1 семестр»

Часть 1 «Матрицы. Линейные системы. Векторы»

выдаётся на 2 нед., сдача на 9 нед.,

Часть 2 «Линии и поверхности» выдаётся на 10 нед., сдача на 18 нед.

 

Содержание 1 семестра:

1. Определение матриц, их сравнение, транспонирование, умножение на число, сумма и разность, произведение матриц.

2. Определители второго и третьего порядка: определение, правило вычисления и основные свойства. Понятие минора и алгебраического дополнения элемента, раскрытие определителя по строке или столбцу.

3. Общее определение определителя n-го порядка. Задача о расстановке ладей на шахматной доске. Вычисление определителя четвертого порядка.

4. Обратная матрица: определение, теорема о существовании обратной матрицы (способ нахождения А^-1), проверка полученного результата.

5. Система линейных уравнений, определение ее решения. Метод Крамера нахождения решений линейной системы. Теорема Крамера. Матричная запись линейной системы. Матричный метод нахождения решения линейной системы.

6. Метод Гаусса и Жордана-Гаусса решения линейной системы. Случаи единственного решения, множества решений и отсутствия решений.

7. Однородная линейная система, существование ее нетривиального решения, базисные и свободные переменные при этом.

 

8. Скалярные и векторные величины. Способы задания векторов. Действия над векторами (графически): сравнение, умножение на число, сумма и разность. Основные свойства действий над векторами.

9. Линейная зависимость системы векторов. Размерность векторного пространства (прямой, плоскости, пространства). Афинный базис, афинные координаты вектора, нахождение их геометрически.

10. Скалярное произведение векторов: определение, основные свойства. Косинус угла между векторами. Модуль вектора. Проекции вектора на ось.

11. Декартова система координат, базисные векторы. Декартовы координаты вектора, запись вектора через базисные. Связь точек и векторов. Сравнение, умножение на число, сумма, разность векторов в координатной форме.

12. Скалярное произведение векторов в декартовых координатах. Модуль вектора, расстояние между точками и угол между векторами в координатной форме.

13. Правая тройка векторов. Векторное произведение: определение и основные свойства, геометрический смысл, синус угла между векторами.

14. Векторное произведение двух векторов в координатной форме. Площадь треугольника, заданного координатами вершин с помощью векторного произведения.

15. Смешанное произведение: определение, основные свойства и правило вычисления в координатной форме, геометрический смысл, проверка линейной зависимости.

 

16. Способы задания линии на плоскости, поверхности и линии в пространстве по Декарту и Жордану. Полярная система координат.

17. Уравнения прямой на плоскости: векторное, параметрическое, через две точки, каноническое, с угловым коэффициентом, общее, в отрезках и нормальное. Связь направляющего и нормального векторов прямой.

18. Взаимное расположение двух прямых на плоскости (по уравнениям), параллельность, перпендикулярность, точка пересечения. Расстояние от точки до прямой. Угол между двумя прямыми. Проекция точки на прямую.

19. Уравнения плоскости в пространстве: векторное, параметрическое, через три точки (точку и два направляющих вектора), общее в отрезках и нормальное.

20. Связь нормального и направляющих векторов плоскости. Взаимное расположение плоскостей (параллельность, совпадение, пересечение, перпендикулярность) по уравнениям. Расстояние от точки до плоскости. Угол между плоскостями.

21. Уравнения прямой в пространстве: векторное, параметрическое, по двум точкам, каноническое, общее, через проектирующие плоскости.

22. Взаимное расположение прямой и плоскости: параллельность, пересечение, перпендикулярность, проекция точки на плоскость, симметрия точки относительно плоскости. Угол между прямой и плоскостью.

 

23. Взаимное расположение двух прямых в пространстве по уравнениям: пересечение (точка пересечения), параллельность (расстояние), скрещивание (наименьшее расстояние).

24. Эллипс: определение, каноническое уравнение, свойства, построение.

25. Гипербола: определение, каноническое уравнение, свойства, построение.

26. Парабола: определение, каноническое уравнение, свойства, построение.

27. Общее уравнение линии второго порядка, приведение к каноническому уравнению по общему (при отсутствии х^.у) выделением полных квадратов.

28. Директориальное свойство эллипса и гиперболы, правило нахождения их канонического уравнения.

29. Нахождение уравнения окружности по трем точкам.

30. Классификация линий второго порядка на плоскости. Цилиндрические и конические сечения.

31. Канонические уравнения и эскизы поверхностей второго порядка: эллипсоида, гиперболоидов, параболоидов.

32. Линейчатые поверхности (гиперболоид и параболоид). Цилиндрические и конические поверхности. Классификация поверхностей второго порядка.

33. Основы модели Леонтьева межотраслевого баланса: матрица коэффициентов прямых затрат, МОБ в количественном и стоимостном выражении, нахождение валового продукта при заданном чистом продукте.

 

 

4.1.2 Семестр – 2 Трудоёмкость 2 ЗЕТ, 72 ч., зачёт

Таблица 4

№ п/п	Название темы/раздела учебной дисциплины	Неделя семестра	Виды учебных занятий, и их трудоемкость (в часах)	Ссылка на ПР УД	Форма контроля
Лекции	Практические занятия	Лабораторные занятия	Самостоятельная работа
10.	Пределы последовательностей и функций	1-2					З3, У3, В3	Дз-2 Часть 1
11.	Производная функции одной переменной	3-4
12.	Свойства дифференцируемых функций	5-6
13.	Экстремумы функции	7-8
14.	Исследование функций и построение их графиков. Задачи на оптимизацию	9-10
15.	Неопределенный и определённый интеграл, их связь	11-12					З3, У3, В3-В4	Дз-2 Часть 2
16.	Основные методы интегрирования	13-14
17.	Применения интегралов	15-16
	Итого:
18.	Зачёт (З-2)

Дз-2 «Задания по математике, 2 семестр»

часть 1 «Пределы, непрерывность, производная функции одной переменной»

выдаётся на 2 нед., сдача на 11 нед.,

часть 2 «Интегрирование» выдаётся на 10 нед., сдача на 18 нед.

Содержание 2 семестра:

1. Определение числовой последовательности и ее предела. Свойства пределов последовательности.

2. Определение функции одной переменной, способы ее задания. Обратная функция, связь графиков взаимообратных функций. основные элементарные функции, их графики и основные свойства.

3. Преобразования, влияющие на график функции ( f(x)+c, f(x+c), c^.f(x), f(c^.x), êf(x)ê, f(êx-cê) ). Графики линейной, параболической, дробно-линейной функции и у=А^.sin(w^.x+w₀).

4. Определение предела функции в точке. бесконечный предел и предел на бесконечности. Свойства пределов.

5. Бесконечно малая функция (БМ). Сравнение БМ: эквивалентность, символ "о". Первый замечательный предел, его применение. Основные эквивалентности БМ в пределах.

6. Бесконечно большая функция (ББ). Сравнение ББ: эквивалентность, символ "о". Шкала ББ при х →∞, её применение.

7. Связь БМ, ББ и других функций. Основные виды неопределенностей в пределах, способы их раскрытия. Второй замечательный предел, правило его применения.

8. Непрерывность функции в точке. Частичные пределы, их связь с непрерывностью. Точки разрыва функции, их классификация.

9. Непрерывность основных элементарных функций. Свойства непрерывных в точке функций.

10. Свойства непрерывных на отрезке функций: сохранение знака, ограниченность, достижение наибольшего и наименьшего значений, поиск корня f(x)=0 методом половинного деления, промежуточные значения.

 

11. Производная функции f(х): определение, геометрический смысл с уравнением касательной и нормали, физический смысл. Свойства производных.

12. Производные основных функций (xⁿ, aⁿ, ln(x), sin(x), cos(x)) c доказательствами.

13. Приращение дифференцируемой функции, понятие дифференциала и его связь с производной. Геометрический смысл дифференциала. Инвариантность формы дифференциала, его применение в приближенных вычислениях.

14. Производная обратной функции. Вывести производные arcsin(x), arctg(x). Производная неявно заданной функции.

15. Логарифмическое дифференцирование. Понятие гиперболических функций, их производные.

16. Свойства дифференцируемых на отрезке функций: теоремы Ферма, Ролля, Лагранжа и Коши.

17. Производные и дифференциалы высших порядков. Формула Тейлора, её коэффициенты и остаточный член в формах Пеано и Лагранжа.

18. вывести разложения sin(x), cos(x), e^x, ln(1+x), (1+x)ⁿ по формуле Маклорена.

19. Производные y_x'(x), y_xx"(x) для функции, заданной параметрически.

20. Определение точки экстремума. Связь монотонности функции и знака ее производной. Теорема Ферма (необходимое условие точек экстремума).

Достаточные условия экстремума:

a) с помощью знака первой производной;

b) с помощью производных старших порядков.

21. Алгоритм нахождения точек экстремума. Вычисление наибольшего и наименьшего значений функции на отрезке, примеры задач на нахождение наибольшего и наименьшего значений функции одной переменной.

22. Определение выпуклой (вогнутой) НА ОТРЕЗКЕ ФУНКЦИИ. Связь выпуклости со знаком второй производной. Алгоритм нахождения точек перегиба.

23. Правило Лопиталя раскрытия неопределенностей в пределах.

24. Понятие асимптоты графика функций, их виды и способы нахождения.

25. Общий план исследования функций и построения графика функции.

26. Нахождение наибольшего (наименьшего) значения функции на ОТРЕЗКЕ.

27. Решение текстовых задач на оптимизацию.

 

28. Определение первообразной для f (x) на [a; b], теорема о двух первообразных. Неопределенный интеграл (НИ), его свойства. Таблица основных интегралов.

29. Определенный интеграл (ОИ) для f( x), как предел интегральных сумм, его основные свойства, теорема о среднем.

30. Интеграл с переменным верхним пределом, теорема о его производной.

31. Формула Ньютона-Лейбница и её применение.

32. Замена переменной в НИ и ОИ.Интегрирование по частям в НИ, ОИ, основные случаи.

33. Вычисление некоторых НИ методом неопределенных коэффициентов.

34. Дробно-рациональная функция, алгоритм ее разложения на сумму элементарных дробей:

а) выделение целой части, алгоритм "деление столбиком";

б) разложение многочлена на неприводимые множители, кратность корня;

в) метод неопределенных коэффициентов разложения на элементарные дроби.

35. Интегралы от элементарных дробей. Общий план интегрирования дробно-рациональных функций.

36. Интегралы от тригонометрических функций; Основные случаи и способы интегрирования данных интегралов.

37. Интегралы от иррациональных функций. Примеры "неберущихся" интегралов.

38. Нахождение площади криволинейной трапеции и площадей плоских фигур с помощью ОИ (ограниченных y_i=f_i(x); параметрических заданными).

39. Площадь криволинейного сектора. Нахождение площади фигуры в полярных координатах.

40. Объем тела по поперечным сечениям. Объем тела вращения с помощью ОИ.

4.1.3 Семестр – 3 Трудоёмкость 3 ЗЕТ, 108 ч., экзамен

Таблица 5

№ п/п	Название темы/раздела учебной дисциплины	Неделя семестра	Виды учебных занятий, и их трудоемкость (в часах)	Ссылка на ПР УД	Форма контроля
Лекции	Практические занятия	Лабораторные занятия	Самостоятельная работа
19.	Функции нескольких переменных	1-3					З4, У4, В5	Дз-3 Часть 1
20.	Экстремумы ФНП.. Задача линейного программирования	4-6
21.	Дифференциальные уравнения	7-8					У3, В3
22.	Интегрирование ДУ 1-го порядка	9-10					З5, У4, В6	Дз-3 Часть 2
23.	Свойства решений линейных ДУ. Метод Эйлера решения ЛОДУ	11-13
24.	Решения линейных ДУ	14-16
25.	Системы ДУ	17-18
	Итого:
26.	Экзамен (Э-3)	Контроль – 18 ч.

 

Дз-3 «Задания по математике, 3 семестр»

Часть 1 «Функции нескольких переменных» выдаётся на 2 нед., сдача на 10 нед.,

Часть 2 «Диф.уравнения. Системы ДУ» выдаётся на 12 нед., сдача на 18 нед.

Содержание 3 семестра:

 

1. Область нескольких переменных, окрестность точки. Открытая и замкнутая области нескольких переменных. Функции нескольких переменных (ФНП): определение, способы задания. Геометрический смысл Z=f(x,y), линии уровня.

2. Предел ФНП в точке. Непрерывность ФНП в точке. Основные свойства непрерывных ФНП.

3. Определение частной производной ФНП, правила их вычисления. Геометрический смысл частных производных для Z=f(x,y). Уравнение касательной плоскости и нормали.

4. Полный дифференциал ФНП, связь с Δf, инвариантность его формы. Полная производная по переменной t. Производная неявной функции.

5. Производная по направлению. Градиент функции: определение, правила вычисления, связь с производной по направлению и с линией (поверхностью) уровня.

6. Частные производные высших порядков. Теорема о смешанных производных ФНП. Дифференциалы высших порядков для ФНП, их коэффициенты для f(x, y) (треугольник Паскаля и бином Ньютона). Формула Тейлора для ФНП. Приближенные вычисления.

7. Точки экстремума ФНП. Необходимое условие экстремума. Достаточное условие экстремума в общем виде и для f(x, y), характер экстремума.

8. Условный экстремум ФНП. Метод множителей Лагранжа и метод подстановки.

9. Нахождение наибольшего и наименьшего значений ФНП в замкнутой ограниченной области (план

10. Задача о производстве нескольких изделий при ограничениях по ресурсам. Графический метод её решения.

 

11. Общие понятия теории обыкновенных дифференциальных уравнений (ДУ): ДУ, его решение, общее и частное решения, начальные и краевые условия, интегральная кривая, задача Коши. Теорема Коши для ДУ первого порядка.

12. ДУ с разделенными и разделяющимися переменными, их решения. Сведение текстовой задачи к решению ДУ на примере задачи о распаде радия и о непрерывном растворении соли (или другой задачи).

13. Однородные функции двух переменных. Общий вид и правило интегрирования однородных диф. уравнений. Уравнения, приводящиеся к однородным, их интегрирование.

14. Линейные ДУ первого порядка, методы Бернулли и Лагранжа для их интегрирования.

15. Уравнение Бернулли, его интегрирование непосредственно и сведением к линейному ДУ.

16. Уравнение в полных дифференциалах: общий вид, правило интегрирования и физический смысл (потенциальность плоского векторного поля).

17. Методы Эйлера и изоклин приближенного построения интегральных кривых.

18. Решение ДУ в виде степенного ряда, два способа нахождения его коэффициентов;

19. ДУ второго порядка. Случаи ДУ, допускающих понижение порядка.

20. Линейное ДУ второго порядка: общий вид, свойства решений, структура общего решения.

21. Линейная зависимость системы функций. Определитель Вронского. Теорема о связи определителя Вронского с линейной зависимостью решений линейного однородного ДУ. Фундаментальная система решений и общее решение при этом.

22. Линейное однородное ДУ с постоянными коэффициентами: общий вид, метод Эйлера его решения, характеристическое уравнение. Общее решение линейного ДУ при известных корнях характеристического уравнения:

а) корни действительные, различные;

б) корни кратные;

в) корни комплексные, сопряженные.

23. Нахождение частного решения линейного неоднородного ДУ при неоднородности специального вида (метод подбора):

а) P_n(x); б) P_n(x)^.e^ax; в) e^ax. (Acos(bx) + Bsin(bx)); г) Сумма функций.

Нахождение коэффициентов предполагаемого решения.

24. Нахождение частного решения линейного неоднородного ДУ методом вариации постоянных.

25. ДУ, описывающее механические колебания. Случаи свободных, затухающих, вынужденных колебаний. Случай резонанса.

26. Каноническая и нормальная формы системы ДУ. Решение системы ДУ, общее и частное решения. Начальные условия. Теорема о существовании и единственности решения системы ДУ.

27. Сведение ДУ к системе ДУ в нормальной форме, системы ДУ к одному дифференциальному уравнению (метод исключения).

28. Системы линейных уравнений, свойства решений однородных систем и неоднородных систем ДУ. Определитель Вронского системы ДУ, его свойства. ФСР системы ЛОДУ.

29. Нахождение решений линейной однородной системы методом исключения.

30. Нахождение решений линейной однородной системы с помощью собственных векторов.

31. Нахождение решений линейной неоднородной однородной системы методом вариации постоянных.

 

4.1.4 Семестр – 4 Трудоёмкость 4 ЗЕТ, 144 ч., экзамен

Таблица 6

№ п/п	Название темы/раздела учебной дисциплины	Неделя семестра	Виды учебных занятий, и их трудоемкость (в часах)	Ссылка на ПР УД	Форма контроля
Лекции	Практические занятия	Лабораторные занятия	Самостоятельная работа
27.	Действия над событиями	1-2					З6 У5, В7	Дз-4 Часть 1
28.	Вероятность событий	3-4
29.	Распределения ДСВ	5-6					З6-З7, У5-У6, В7
30.	Функция и плотность распределения НСВ	7-8
31.	Распределения НСВ	9-10
32.	Нормальное распределение	11-12
33.	Анализ одномерных выборок	13-14					З8, У7, В8	Дз-4 Часть 2
34.	Проверка статистических гипотез. Общий план обработки стат.данных	15-16
35.	Корреляция	17-18
	Итого:
36.	Экзамен	Контроль 9 ч.

Дз-1 «Задания по дисциплине, 4 семестр» разбита на 2 части:

Дз-1 часть 1 «Вероятность. Случайные величины»

выдаётся на 2 нед., сдача на 12 нед.,

Дз-1 Часть 2 «Статистика. Корреляция»

выдаётся на 13 нед., сдача на 18 нед.,

 

Содержание 4 семестра:

1. Понятие испытания и случайного события. Основные виды испытаний и событий. Действия над событиями: равенство, сумма, произведение, противоположное событие (определения и диаграммы) и их основные свойства.

2. Частота и относительная частота события, статистическое определение вероятности события. Свойства вероятности. Понятие исходов испытания, классическое определение вероятности события. Отличие статистического и классического определений вероятности.

3. Элементы комбинаторики: сформулировать определения и вывести способы вычисления чисел перестановок, размещений, сочетаний и их основные свойства.

4. Вывести формулу вероятности суммы совместных и несовместных событий, формулу включения-исключения.

5. Сформулировать определения зависимых и независимых событий, условной вероятности. Вывести формулу вероятности произведения событий. Примеры зависимых и независимых событий, вероятности их произведения.

6. Сформулировать определение гипотез, вывести формулу полной вероятности и правило её применения.

7. Вывести формулу Байеса и правило её применения.

8. Описать схему Бернулли повторения испытаний. Вывести формулу Бернулли и правило её применения. Наивероятнейшее число появлений события.

9. Геометрическая вероятность, условия её применения. Формулировка и решение задачи о встрече.

10. Определение случайной величины, отличие дискретных случайных величин (ДСВ) от непрерывных случайных величин (НСВ), их примеры. Закон распределения ДСВ, способы вычисления и основные свойства математического ожидания ДСВ.

11. Определение, вычисления для ДСВ и основные свойства дисперсии D(x) и 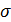(x).

12. Вывести М(х), D(x) и 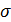(x) для биномиального распределения.

13. Определение и основные свойства функции распределения F(x).

14. Определение и основные свойства плотности распределения f (x) для НСВ.

15. Сформулировать правила вычисления М(х), D(x) и 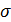(x) для НСВ и их основные свойства.

16. Вывести параметры плотности распределения, функцию распределения для равномерного распределения, найти М(х), D(x) и 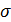(x) для него. Вероятность попадания в указанный промежуток.

17. Вывести параметры плотности распределения, функцию распределения для показательного распределения, найти М(х), D(x) и 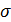(x) для него. Функция надёжности. Вероятность попадания в указанный промежуток.

18. Записать плотность распределения нормированного и ненормированного нормального распределения, использование таблиц для вычисления их значений. Влияние параметров нормального распределения на вид нормальной кривой.

19. Вероятность попадания Х с нормальным распределением в указанный промежуток, правило «трёх сигма». Нахождение вероятности отклонения.

20. Центральная предельная теорема. Закон больших чисел.

21. Сформулировать локальную и интегральную теоремы Лапласа, вывести свойства функций 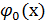,Ф(х), использование их таблиц. Нахождение вероятности отклонения.

22. Цели и задачи математической статистики. Выборочный метод: понятие выборки, её объёма, способы отбора её элементов, репрезентативность.

23. Графическое представление выборки (в зависимости от способа представления): полигон, гистограмма, выборочные плотность и функция распределения, диаграммы и картограммы.

24. Нахождение числовых характеристик выборки: среднего выборочного, выборочной дисперсии, s_в, моды и медианы (общие и сгруппированные).

25. Виды статистических оценок: несмещённые, эффективные и состоятельные оценки (на примере М(х) и D(x)).

26. Применение критерия согласия Пирсона для проверки статистической гипотезы. Нахождение параметров равномерного, показательного, Пуассонова и нормального распределений по выборочным данным.

27. Общий план обработки статистических данных.

28. Зависимость и независимость случайных величин, стохастическая и функциональная составляющие зависимости. Корреляционная зависимость.

29. Постановка задачи и применение метода наименьших квадратов, нахождение параметров кривой Y(x) (общий случай).

30. Вывести правило нахождения параметров линейной регрессии по выборочным данным с помощью метода наименьших квадратов, его связь с результатами корреляционного анализа.

31. Вывести правило нахождения параметров параболической регрессии по выборочным данным с помощью метода наименьших квадратов.

32. Правило составления корреляционной таблицы по выборочным данным.Правила нахождения средних (центра корреляции), условных средних и построения эмпирической линии регрессии по корреляционной таблице.