Урок 9
Тема: Равномерное движение тел по окружности. Кинематика абсолютно твёрдого тела.
Цели урока:
Изучить равномерное движение тела по окружности и познакомить учащихся с основными характеристиками данного движения.
Задачи урока:
Образовательная
(Обучающие: продолжить формирование представлений о движении тела; сформировать у учащихся представления о характеристиках равномерного движения по окружности. Развивающие: продолжить работу по формированию ключевых компетенций учащихся: умения сравнивать, анализировать, делать выводы из наблюдений, обобщать опытные данные на основе имеющихся знаний о движении тела;
развивать способность обобщать и представлять разнообразную информацию в рамках общей поставленной задачи;
формировать умения использовать основные понятия, формулы и физические законы движения тела при движении по окружности;
развивать физическое мышление учащихся через практическую деятельность; развивать умения сравнивать и анализировать.
Воспитывающие: воспитывать самостоятельность; научить детей сотрудничеству;
воспитывать уважение к мнению других (работа в группе)
Ход урока
Организационный момент
Актуализация знаний
В начале занятия давайте проведем физическую разминку. Повторим основные понятия кинематики.
Вопросы разминки:
1. Какое движение называют равномерным?
2. Что называют скоростью равномерного движения?
3. Какое движение называют равнопеременным?
4. Что такое ускорение тела?
5. Что такое путь и перемещение?
6. Какие типы траектории Вам известны?
7. При каком движении путь и перемещение совпадают? Не совпадают?


Задача 1 Почему бомба, сброшенная с горизонтально летящего самолета, не падает вертикально вниз?
|
|
Решение:
Бомба, как и самолет, имеет скорость в горизонтальном направлении и в момент отрыва от самолета вследствие инерции удерживается в этом состоянии движения.
Задача 2. Снаряд вылетает из горизонтально направленного ствола пушки с некоторой скоростью. С какой скоростью вылетел бы тот же снаряд из той же пушки, если бы выстрел был произведен также горизонтально на поверхности Марса, сила притяжения которого составляет 0,38 силы притяжения Земли? Трением в стволе пушки пренебречь.
Решение:
Скорость движения снаряда зависит от величины силы, действующей на снаряд, и от массы снаряда, но не зависит от силы тяжести. Более слабое притяжение Марса повлияло бы на дальность полета снаряда и на форму его траектории движения. Поэтому снаряд будет вылетать из пушки с одинаковой скоростью и на Марсе, и на Земле.
Задача 3. С башни в горизонтальном направлении бросили камень с начальной скоростью 10 метров в секунду. Камень упал на расстоянии 40 метров от основания башни. Сколько времени камень находился в полете?
Дано Решение:
V0=10 м/с  S=40м
S=40м 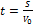 t= 4 c
t= 4 c
t-? Ответ: t= 4 c
Задача 4. Шарик катился по гладкой горизонтальной поверхности стола со скорость 2 метра в секунду. Докатившись до края стола, шарик падает на пол на расстоянии 0,8 метров от основания стола. С какой высоты упал шарик?
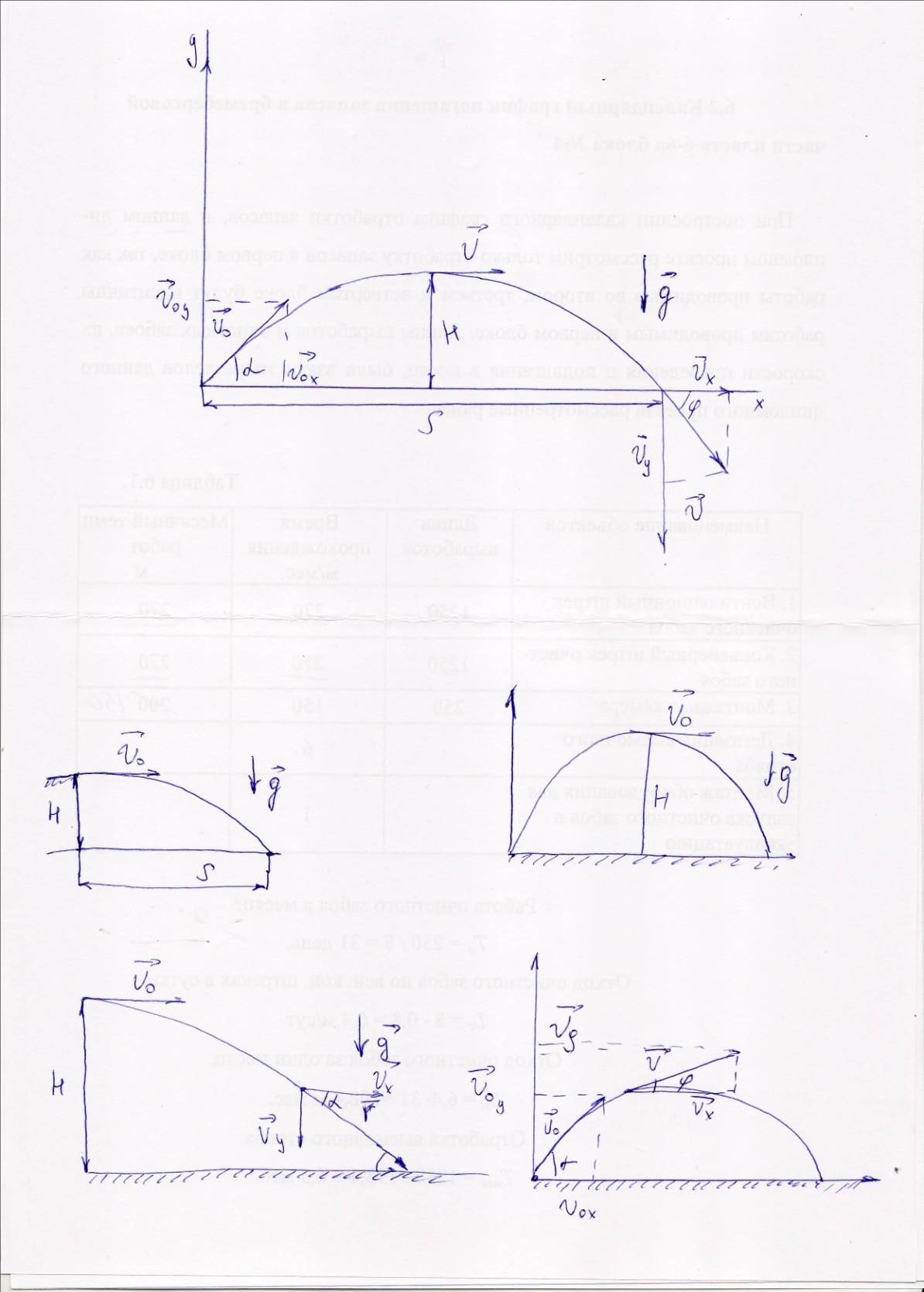 Дано Решение:
Дано Решение:
g=10 м/с2 S = V*t, V = V0 t = S/V0= 0.4 м/с
S=0,8 м 
V=2 м/с
H-? Ответ: H=0.8 м
Задача 7. Мальчик бросил горизонтально мяч из окна, расположенного на высоте 15 м. Сколько времени летел мяч до земли и с какой скоростью он был брошен, если мяч упал на расстоянии 5,3 м от основания дома?
|
|
Дано:
h = 15 м;
l=5,3м;
g = 9,8 м/ 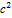
| Решение:
Для описания движения выберем прямоугольную систему координат х0у, ось у направим вертикально вниз. За начало отсчета координат О примем точку бросания мяча.
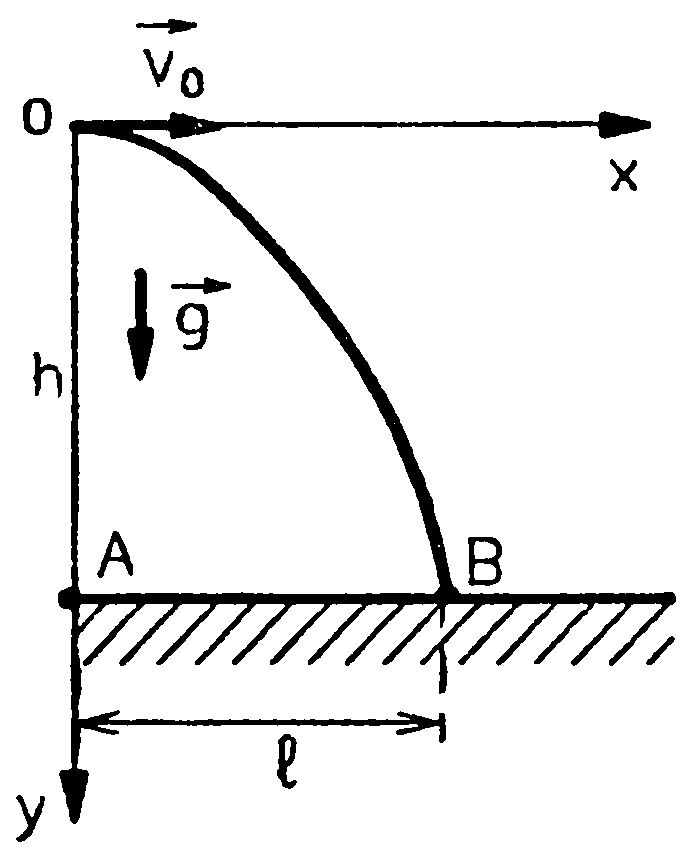 Уравнения движения мяча:
0x: x = Уравнения движения мяча:
0x: x = 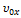 t
0y: y = t
0y: y = 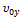 t + t + 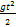 По условию задачи
По условию задачи 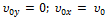 , следовательно:
x = , следовательно:
x = 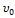 t
y = t
y = 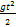 В момент приземления
y = h; x = l.
Тогда определим время полета и начальную скорость:
В момент приземления
y = h; x = l.
Тогда определим время полета и начальную скорость:
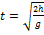 ; ; 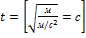
 Вычислим:
Вычислим:

 или или
 Ответ:
Ответ:  , , 
|
Задача 5 Кошка прыгает с подоконника высотой 1,2 метра горизонтально со скоростью 6 метров в секунду. На какое расстояние от стены она окажется на момент приземления.
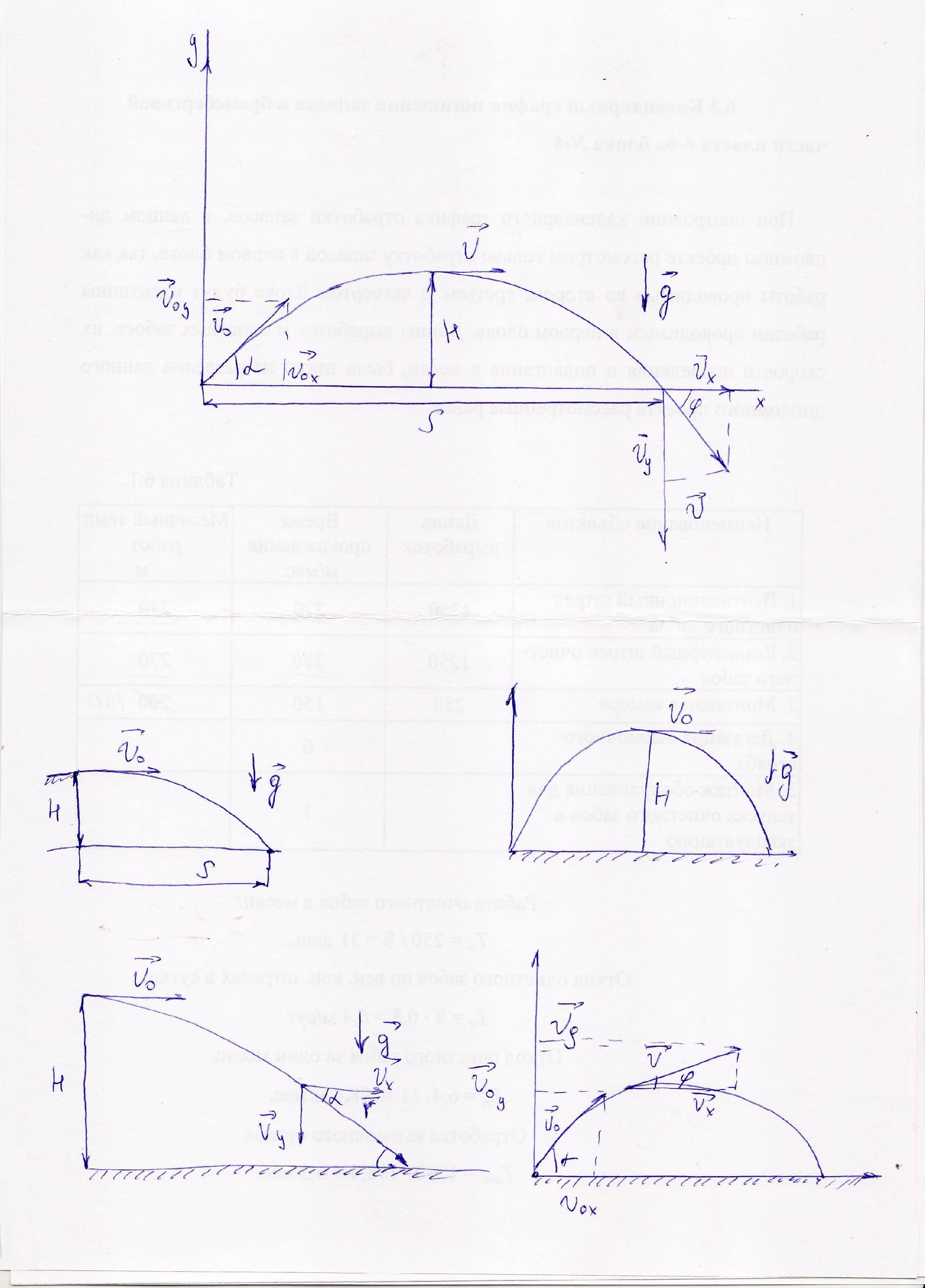 Дано Решение:
Дано Решение:
g =9.8 м/с2 S=V0t H=gt2/2 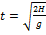
V0=6 м/с H=1,2 м
S-? 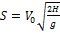
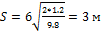
Ответ: S=3 м
2. Объяснение нового материала При криволинейном движении путь и перемещение не совпадают. Давайте рассмотрим данное движение более подробно
Угловая скорость
Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

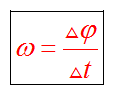
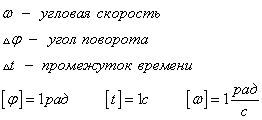
Период и частота
Период вращения T - это время, за которое тело совершает один оборот.
Частота вращение - это количество оборотов за одну секунду.

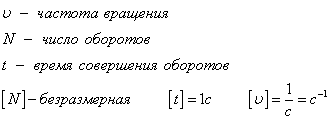
Частота и период взаимосвязаны соотношением


Связь с угловой скоростью

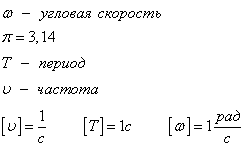
Линейная скорость
Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.
|
|

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено - это есть период T. Путь, который преодолевает точка - это есть длина окружности.

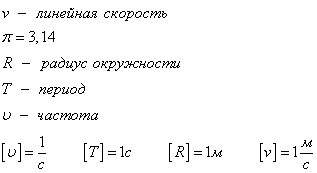
Центростремительное ускорение
При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

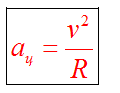

Используя предыдущие формулы, можно вывести следующие соотношения
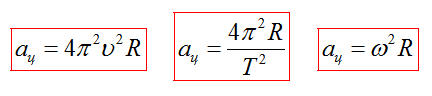
Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.