Основные требования к курсовой работе
Курсовая работа по дисциплине «Бизнес-статистика» выполняется по теме «Применение статистических методов анализа в бизнесе».
Написание работы предполагает ознакомление студента с публикациями по теме исследования. Все теоретические положения, приводимые в работе должны сопровождаться ссылкой на литературный источник (монографии, статьи, учебные издания, Интернет-ресурсы и т. п.). Не следует использовать в качестве единственного источника учебное пособие по дисциплине – выполнение курсовой работы предполагает более глубокое изучение избранной темы.
Структура курсовой работы является типовой и включает следующие элементы:
- титульный лист, который оформляется в соответствии с приложением;
- задание, которое оформляется в соответствии с приложением;
- содержание;
- введение;
- основная часть;
- заключение (выводы);
- список использованных источников;
- приложения (при необходимости).
Во введении обосновывается актуальность выбранной темы, определяется общая цель курсовой работы, ее конкретные задачи и методы исследования.
Основная часть содержит: теоретический раздел (главу), прикладную часть (главу).
Теоретический раздел посвящается представлению сущности теоретических аспектов выбранного для разработки метода бизнес-статистики. В ней приводятся цифровые примеры использования этого метода в конкретных бизнес приложениях. Прикладная часть носит практический характер, в ней формируется и исследуется статистическая модель для решения поставленных в работе задач.
Курсовая работа должна быть оформлена в соответствии с требованиями к оформлению работ ИБМТ БГУ.
|
|
Объем работы – до 20 страниц компьютерного текста шрифта Times New Roman 14 размера через 1,5 интервала на бумаге формата А4 (210 х 297 мм). Приложения в указанный объем не входят.
Выполнение курсовой работы предполагается по следующим основным методам Бизнес-статистики:
· Метод средних величин и показателей вариации;
· Выборочный метод;
· Метод рядов динамики (временных рядов);
· Индексный метод;
· Корреляционно-регрессионный анализ.
Все предложенные методы рассматриваются с точки зрения возможности использования теоретических сведений, приобретенных в процессе их изучения, для решения поставленных задач. Остановимся более подробно на особенностях предложенных для написания курсовой работы методов Бизнес-статистики.
Методы Бизнес-статистики
Методы Бизнес-статистики используются в различных областях бизнеса для принятия решений на основе количественной информации. С их помощью получаются точные количественные характеристики рыночной ситуации и проводится ее исследование и прогнозирование. Путем применения статистических методов для обработки показателей имеющиеся данные о бизнес-среде помогают менеджерам, экономистам, маркетологам и всем другим специалистам понимать процессы развития компании, оценивать ее перспективы.
Целью курсовой работы является использование студентом теоретических знаний статистических методов анализа для развития практических умений и навыков в конкретных бизнес-приложениях.
В ходе выполнения курсовой работы предполагается применять статистические методы:
Метод средних величин и показателей вариации;
|
|
Выборочный метод;
Метод рядов динамики (временных рядов);
Индексный метод;
Корреляционно-регрессионный анализ.
Далее приведем краткую характеристику указанных методов.
Метод средних величин и показателей вариации
Средние величины – это обобщающие показатели, в которых находит выражение действие общих условий, закономерность изучаемого явления.
Например, выбор инвестиционной стратегии должен начинаться с анализа среднегодовой доходности фондов за ряд последних лет. Целесообразно сравнивать доходность фондов, имеющих разную степень риска.
В большинстве случаев данные концентрируются вокруг некоей центральной точки. Таким образом, для описания любого набора данных, достаточно указать некое типичное значение. Эту величину называют средним значением.
Вариация – количественное изменение величины исследуемого признака в пределах однородной совокупности, которое обусловлено перекрещивающимся влиянием действия различных факторов.
Такие показатели вариации как дисперсия и среднее квадратическое (стандартное) отклонение позволяют оценить разброс данных вокруг среднего значения, т.е. сколько элементов выборки меньше среднего, а сколько – больше. Дисперсия обладает ценными математическими свойствами. Однако ее величина представляет собой квадрат единицы измерения (квадратный %, квадратный доллар и т.д.). Поэтому естественной оценкой дисперсии является стандартное отклонение, которое выражается в обычных единицах измерения - %, доллары…
Стандартное отклонение позволяет оценить величину колебания индивидуальных значений вокруг среднего. Практически во всех ситуациях наблюдаемые величины лежат в интервале плюс-минус одно стандартное отклонение от среднего значения. Поэтому, зная среднее арифметическое и среднее квадратическое (стандартное) отклонение можно определить интервал, которому принадлежит основная масса данных.
|
|
Определяются три вида дисперсии:
- общая дисперсия 
,
- межгрупповая дисперсия 
,
- средняя внутригрупповых дисперсий 
.
Общая дисперсия характеризует вариацию признака, которая зависит от всех условий в данной совокупности:
где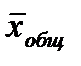 
- общая средняя для всей изучаемой совокупности.
Межгрупповая дисперсия отражает вариацию изучаемого признака, которая возникает под влиянием признака фактора, положенного в основу группировки,
Где:
- средняя по отдельным группам;
- средняя общая;
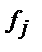- численность отдельных групп.
Средняя внутригрупповых дисперсий характеризует случайную вариацию в каждой отдельной группе. Это вариация результативного признака, которая возникает под влиянием всех остальных факторов, кроме группировочного.
где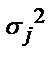 
- дисперсия в каждой группе.
Большую практическую значимость имеет правило сложения дисперсий:
.
Коэффициент детерминации h2 находят по формуле:
.
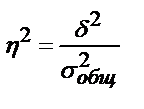Он характеризует долю вариации группировочного признака в общем объеме вариации или на сколько процентов уровень результативного признака определяется группировочным признаком.
Выборочный метод
Практические исследования не всегда имеют дело с данными сплошного наблюдения. Из всех видов не сплошного наблюдения главным является выборочное наблюдение, т. к. только выборка позволяет распространить данные, полученные по части совокупности, на всю совокупность.
Под выборочным понимается метод статистического исследования, при котором обобщающие показатели изучаемой совокупности (генеральной совокупности) устанавливаются по некоторой её части (выборочной совокупности или просто выборке) на основе положений случайного отбора.
В проведении ряда исследований выборочный метод является единственно возможным, например, при контроле качества продукции (товара), если проверка производится с уничтожением или разложением на составные части обследуемых образцов.
Выборочный метод использует два основных вида обобщающих показателей:
- относительную величину альтернативного (качественного) признака.
Она характеризует долю (удельный вес) единиц в статистической совокупности, которые отличаются от других единиц только наличием изучаемого признака (доля нестандартных изделий во всей партии товара);
- среднюю величину количественного признака.
Это обобщающая характеристика варьирующего признака, который имеет различные значения у отдельных единиц статистической совокупности (средняя цена акции; средняя выработка; средняя оплата труда).
Определим следующие величины для генеральной совокупности:
- доля единиц с изучаемым признаком (генеральная доля) Р;
- средняя величина варьирующего признака (генеральная средняя) 
.
И для выборки:
- доля изучаемого признака (выборочная доля или частота) w;
- средняя величина в выборке 
(выборочная средняя).
Тогда основная задача выборочного обследования состоит в том, чтобы на основе характеристик w и 
из выборки получить достоверные суждения о Р и 
в генеральной совокупности. Их расхождения измеряются средней ошибкой выборки m.
При изучении доли альтернативного признака показатели в генеральной совокупности соотносятся следующим образом:
,
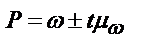При изучении средней величины:
.
Величина коэффициента доверия t зависит от доверительной вероятности и определяется по специальным таблицам, исчисленным применительно к случаю нормально распределенной совокупности (таблицы интегральной функции Лапласа).