ТЕОРЕТИЧЕСКАЯ ЧАСТЬ
Опыт и элементарная теория показывают, что показатель преломления газов зависят от плотности. При прочих неизменных условиях зависимость эта может быть представлена следующим выражением:
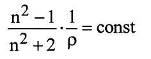 (1)
(1)
где р - плотность газа.
Так как n для газа отличается от 1 лишь в четвертом знаке после запятой, то приближенно можно положить:
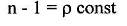 (2)
(2)
Для газов ρ ~ Р, где Р - давление газа. Поэтому n-1 = k0P, где k0-некоторая константа. Было показано, что k0= 2πα/kТ (см. описание 17), где k - постоянная Больцмана, Т - температура, ά -поляризуемость молекулы.
Т. к. воздух есть смесь газов, то под поляризуемостью молекул понимают среднюю величину, определяемую соотношением:

Зная α, можно для различных условий (Т,р) вычислить показатель преломления.
Дифракция Фраунгофера на двух щелях
Измерение показателя преломления в данной работе проводится с помощью интерферометра Рэлея. Устройство интерферометра основано на дифракции Фраунгофера на двух щелях.
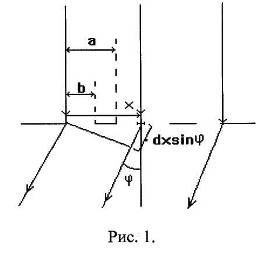
Пусть на экран с двумя щелями нормально падает плоская монохроматическая волна. Рассмотрим дифракционную картину Фраунгофера за экраном. Рассчитаем интенсивность световых колебаний в волне, направление распространения которой составляет угол φ с нормалью к экрану (рис. 1.). Применим для расчета принцип Гюйгенса-Френеля.
Элемент щели dx посылает в направлении φ волну с амплитудой, пропорциональной dx. Фаза колебаний, приходящих в точку наблюдения от элемента с координатой х отстает от колебаний, исходящих из элемента с х=0, на величину kх sinφ (k - волновое число). Колебание dE в точке наблюдения, вызванное нашим элементом dx, может быть записано поэтому в виде
 (3)
(3)
где Ео - некоторый коэффициент пропорциональности. Найдем результат суммарного действия всех элементов обеих щелей. Для этого надо проинтегрировать выражение (3) по значениям х, соответствующим открытым частям экрана. При этом будем считать, что угол φ достаточно мал (sin φ ≈ φ) и что в правой щели искусственно создана дополнительная разность хода Δ, одинаковая для всех ее элементов (это позволит написать смещение интерференционных полос, используемое для измерений в интерферометреРэлея).
Интегрируя (3), найдем
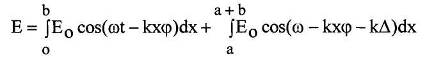 (4)
(4)
где а - расстояние между щелями, b - ширина щели. Элементарные вычисления дают
 (5)
(5)
Интенсивность световых колебаний I равна квадрату их амплитуды
 (6)
(6)
здесь IО=ЕО2b2 - интенсивность света, возникающего в центре дифракционного пятна в том случае, когда открыта только одна из щелей.
Как видно из (6), зависимость I от φ распадается на произведение двух сомножителей. Первый из них описывает распределение интенсивности в дифракционной картине Фраунгофера от одной щели. Второй сомножитель обусловлен интерференцией световых колебаний, приходящих в точку наблюдения от разных щелей. Практический интерес представляют яркие интерференционные полосы, расположенные в пределах первого дифракционного максимума, т.е. в области
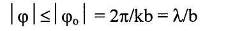
b- ширина щели
Интерференционные максимумы отстоят друг от друга на равные угловые расстояния δφ
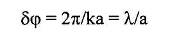
а - расстояние между щелями (вывод этих простых соотношений предоставляются читателю). В пределах первого дифракционного максимума располагается No интерференционных полос
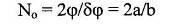 (7)
(7)
Картина зависимости I от φ представлена на рис. 2. Смещение интерференционных полос от середины центрального дифракционного максимума (φ=0) определяется сдвигом фаз Δ и равно Δ/а.
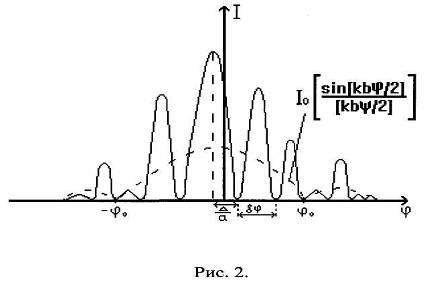
Если одну из щелей закрыть, то наблюдаемое распределение интенсивности опишется сомножителем (6), т. е. пунктирной кривой (рис. 2.). Если закрыть другую щель (а первую открыть), то центральный дифракционный максимум расположится, конечно, в том же самом месте, так что дифракционные картины от каждой из щелей точно накладываются друг на друга (что и является признаком дифракции Фраунгофера). При ознакомлении с интерферометром Рэлея такие опыты полезно проделать.
ПРАКТИЧЕСКАЯ ЧАСТЬ