Рассмотрим систему N тел или материальных точек с массами 
, положение которых относительно произвольной точки О (полюса) задается радиус-векторами 
(рис.16).
Рис.16
Под центром массC системы тел понимают точку, в которой сосредоточена вся масса системы 
, положение 
которой относительно выбранного полюса О задается соотношением
.
Любая система тел с известным положением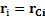 
их центров масс может быть заменена системой материальных точек, положение 
общего центра масс C которых может быть вычислено по приведенной формуле.
Это векторное равенство может быть спроецировано на оси X,Y,Z, произвольно выбранной системы координат XYZ с началом в полюсе О
,
где 
– координаты центра масс С в выбранной системе координат XYZ.
Для тела с распределенной массой положение его центра масс С относительно полюса О и его координаты в выбранной системе отсчета XYZ рассчитываются по формулам
.
Центр масс движется со скоростью 
и ускорением 
, равными
, 
,
где 
и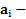 
скорость и ускорение i-го тела системы.
Пример 1. Найти положение центра масс квадрата со стороной l, массы сторон которого равны m, 2m, 3m, 4m.
Дано: l, 
Найти: 
Решение: Пронумеруем стороны квадрата в соответствии с их массами. Выберем начало О системы координат в центре квадрата, ось X направим от О к центру третьей стороны, а ось Y - от О к центру второй. Заменим стороны квадрата материальными точками, находящимися в центрах его сторон. В этой системе координат положения центров сторон квадрата равны
Координаты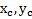 
и положение 
центра масс C квадрата относительно его центра О (полная масса квадрата 
равны
Угол 
между направлением вектора 
и осью X определяется условием 
, то есть 
Ответ: 
Пример 2. Найти положение ЦМ равностороннего треугольника высотой 
.
Дано: . Найти: 
Решение: Выберем начало О системы координат в вершине треугольника, ось 
направим вдоль его высоты (рис.17). Площадь треугольника равна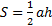 
, а масса 
.
Рис.17
В качестве элемента массы возьмем полоску на расстоянии z от точки О шириной dz, параллельную основанию a. Длина полоски 
, ее площадь 
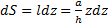, а масса 
. Тогда положение ЦМ треугольника относительно его вершины
Ответ: 
относительно вершины треугольника.
Пример 3. Найти положение центра масс прямого конуса высотой h и радиусом основания R.
Дано: h, R. Найти: 
.
Решение: Выберем начало О системы координат в вершине конуса. Ось Z направим по его оси симметрии к его основанию, а оси X и Y перпендикулярно к оси Z в произвольных направлениях (рис.18). Масса конуса 
.
Рис.18
В качестве элемента массы dm выберем диск радиуса r, на расстоянии z от его вершины, толщиной dz, плоскость которого параллельна его основанию. Тогда 
Координаты центра масс C конуса из симметрии задачи 
Ответ: Центр масс конуса находится на расстоянии 
от его вершины.
Пример 4. Найти положение центра масс полусферы радиуса R относительно ее основания.
Дано: R. Найти: .
Решение: Выберем начало О системы координат в центре полусферы. Ось Z направим по ее оси симметрии перпендикулярно к ее основанию, а оси X иYперпендикулярно к оси Z в произвольных направлениях (рис.19).Масса полусферы 
. В качестве элемента массы dm выберем диск радиуса 
, на расстоянии z от центра полусферы, толщиной dz, плоскость которого параллельна основанию полусферы. Тогда 
Координаты центра масс C полусферы из симметрии задачи
Ответ: 
Рис.19
Пример 5. Найти положение ЦМ половины диска радиуса R.
Дано: R. Найти: .
Решение: Выберем начало О системы координат в центре диска. Ось Z направим вдоль оси симметрии половины диска к его вершине (рис.20).
Рис.20
Масса полукруга 
, где 
– поверхностная плотность массы. В качестве элемента массы выберем стержень на расстоянии z от точки О длиной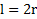 
, где . Ширина стержня dz, площадь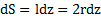 
, а масса 
. При 
– 
и 
. Тогда положение ЦМ полукруга на оси Z
.
Ответ: 
.
Пример 6. Найти положение ЦМ кругового сектора радиуса R с углом при вершине равным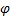 
.
Дано: 
. Найти: 
Решение: Начало О системы координат возьмем в центре кругового сектора, а ось Z направим вдоль его оси симметрии (рис.21). Масса сектора 
,где – поверхностная плотность его массы.
Рис.21
Задачу будем решать в полярной системе координат. В качестве элемента массы dmвыберем площадку, находящуюся на расстоянии rот точки О под углом α к оси X, перпендикулярной оси Z симметрии сектора. Ее координата по оси Z равна 
, площадь 
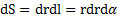, а масса 
.
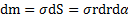Положение 
ЦМ кругового сектора на оси Z относительно точки О, боковые стороны которого составляют углы 
с осью X 
, с учетом, что 
, равно
.
Для половины диска 
приходим к результату примера 5: 
.
Ответ: 
.
Силы в механике
Сила 
– это векторная мера взаимодействия тел (скалярной мерой взаимодействия является потенциальная энергия тела 
).
Любая сила характеризуется ее величиной, направлением и точкой приложения. Осуществлять параллельный перенос начал векторов сил, действующих на тело, в одну точку в задачах на поступательное движение тела нежелательно, а в задачах на вращательное движение тела вообще нельзя, так как это приведет к неправильному решению задачи.
К механическим силам, действующим на тело, относятся:
1. Реакции связейN, T, R и т.д. Связь (опора) – это любое тело, ограничивающее движение другого тела (поверхность какого-либо тела, нить). Реакции связей не имеют конкретного способа вычисления и их находят из второго закона Ньютона.
2. Сила трения скольжения 
, где μ – коэффициент трения тела о поверхность связи, N – нормальная реакция связи. Силу трения покоя находят из условия равновесия тела на поверхности. Силу трения качения и скольжения тела 
находят из основных динамических принципов: второго закона Ньютона или основного закона динамики вращательного движения.
3. Гравитационная сила или сила тяжести согласно закону всемирного тяготения Ньютона
где γ – гравитационная постоянная, M и m – гравитационные массы взаимодействующих тел, r –расстояние между их центрами. Если M – масса планеты, то g – это ускорение свободного падения на расстоянииr от центра планеты. Для планеты радиуса R (для Земли 
) ускорение свободного падения на высоте h от поверхности планеты равно
где 
– ускорение свободного падения на поверхности планеты. Для Земли 
Масса тела, входящая в закон всемирного тяготения, называется гравитационной, а входящая во второй закон Ньютона – инертной. Это разные массы. Равенство единиц измерения инертной и гравитационной масс достигается соответствующим опытным выбором гравитационной постоянной 