Лабораторная работа 3
Вариант 2
ПЛАН
I. Классическая транспортная задача. Решить и проанализировать ТЗ без ограничений.
II. Транспортная задача с ограничениями. Решить ТЗ с запретом перевозки по самому выгодному пути (с наименьшими затратами).
III. Двухэтапная транспортная задача. Решить двухэтапную ТЗ с числом поставщиков – 3, складов – 2 и потребителей – 4, взяв за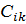 
первых два столбца коэффициентов исходной матрицы, а за 
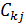– последние две строки этой матрицы. Мощности складов одинаковы и равны половине суммарных запасов поставщиков, округлённых до целых десятков в большую сторону.
I. Классическая транспортная задача
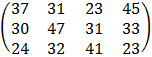
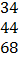
Решается следующая задача (рисунок 1.1).
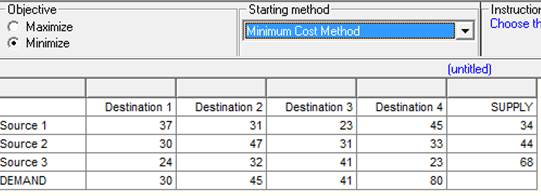
Рисунок 1.1 – Окно исходных данных ТЗ
Центральная часть таблицы – это тарифы по перевозке единицы груза от поставщика к потребителю. Последний столбец (SUPPLY) – запасы груза у поставщика, последняя строка (DEMAND) – спрос потребителя. Как видим, суммарный спрос равен 196, а суммарное предложение – 146 ед. груза. Начальный метод заполнения исходного решения – метод минимальной стоимости.
Решив задачу, можно вывести на экран и сохранить следующие окна:
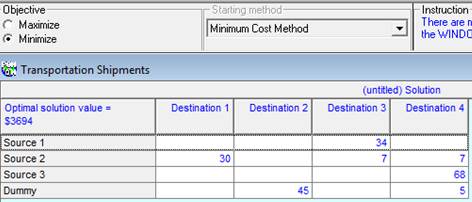
Рисунок 1.2 – Оптимальный план перевозки груза
В этом окне (рисунок 1.2) отражены поставки груза в оптимальном решении ТЗ (от поставщиков к потребителям). В заголовке таблицы указано значение целевой функции в оптимальном решении (Optimal solution value = $3694) – это минимальная стоимость по перевозке. Кроме того, в верхней части отчёта указан метод нахождения начального решения.
Как видно из приведённого отчёта, алгоритм решения задачи ввёл в рассмотрение дополнительного поставщика (последняя строка Dummy) с предложением, равным 50, и поставки от этого поставщика к 2-му и 4-му потребителям означают их неудовлетворенный спрос.
|
|
Как отмечалось, алгоритм решения ТЗ предусматривает равенство суммарного предложения и суммарного спроса и в случае нарушения этого условия вводятся либо фиктивный поставщик (как в нашем случае), либо фиктивный потребитель (если суммарные потребности больше суммарного спроса) с нулевыми тарифами.
Следующее окно (рисунок 1.3) – это оценки свободных клеток таблицы ТЗ в оптимальном решении.
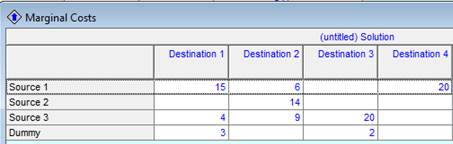
Рисунок 1.3 – Оценки свободных клеток
Эти оценки являются аналогом двойственных оценок задачи ЛП и показывают, насколько изменится целевая функция, если в соответствующую клетку таблицы перераспределить поставку, равную единице. Поскольку все оценки неотрицательны, то это и есть оптимальных план – любое его изменение не приведёт к уменьшению общих затрат по перевозке груза от поставщиков к потребителям. По этой же информации можно судить о числе оптимальных базисных решений – по числу нулевых оценок: в этом примере имеем единственное оптимальное базисное решение.
II. транспортная задача с ограничениями
Предположим, что 2-ой поставщик и 1-й потребитель не связаны между собой прямым маршрутом и поставка между ними не возможна. Для решения задачи в таком виде для запрета поставки между поставщиками и потребителями вводятся «запретительные» тарифы. По сути это «большие» тарифы и алгоритм ТЗ поставку в эту клетку не осуществит, т.к. он нацелен на минимизацию целевой функции. В нашем случае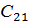 
поставим равным 999. Тогда решение задачи с изменённым тарифом примет вид (рисунок 1.4).
|
|
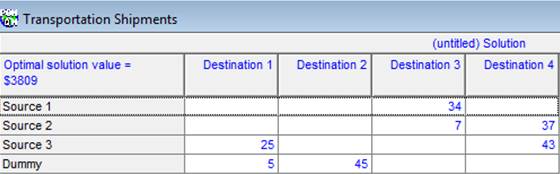
Рисунок 1.4 – Решение ТЗ с запретом
Как видим, клетка (2,1) пуста, т.е. поставка в эту клетку отсутствует, а значение целевой функции увеличилось на 115 за счёт перераспределения поставок по менее выгодным маршрутам.