Импульс системы тел сохраняется 
или 
в двух случаях: если система тел замкнутая 
и в быстрых процессах (взрыв, распад системы, столкновения тел), для которых интервал времени протекания процесса 
. Это следует из второго закона Ньютона в дифференциальной и интегральной форме
, 
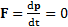Если выполняется условие 
, то говорят о замкнутости системы в направлении оси X и сохранении импульса системы в направлении этой оси: 
Если начальный импульс системы тел равен нулю и он сохраняется, то есть
(в любой момент t),
то положение ЦМ системы сохраняется: 
.
Если система замкнута в направлении оси X и ее начальный импульс равен нулю, то в этом случае сохраняется положение ЦМ системы в направлении этой оси: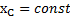 
.
Пример 1. Человек массой m переходит с одного конца лодки массой M и длиной l на другой ее конец со скоростью 
относительно лодки. Найти скорость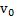 
лодкии ее перемещение x относительно земли, когда человек перейдет на другой конец лодки.
Дано: m, M, l, 
. Найти: 
Решение: Система (лодка и человек +вода) является замкнутой и, в частности, замкнутой в направлении оси X, параллельной поверхности воды (рис.36). Поэтому в системе лодка-человек имеет место закон сохранения импульса, который в начальный момент времени был равен нулю. Наличие сил трения между лодкой и водой не нарушает замкнутость системы в направлении оси X и не влияет на величину перемещения лодки относительно воды.
Рис.36
Во избежание ошибок в знаках проекций векторов задачу будем решать в векторной форме. При движении человека по лодке со скоростью 
лодка придет в движение со скоростью 
относительно берега реки и станет движущейся системой отсчета, и скорость человека относительно земли будет равна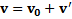 
. Закон сохранения импульса в системе лодка-человек в системе отсчета, связанной с землей, имеет вид
.
Откуда скорость лодки относительно берега равна 
. Знак (
) означает анти параллельность векторов и . В скалярной форме 
.
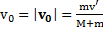Умножая обе части этого равенства на время t движения человека по лодке и обозначая 
и 
, получим для смещения лодки относительно берега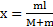 
.
Второй способ решения задачи основывается на сохранении положения ЦМ системы лодка-человек, если ее начальный импульс был равен нулю и сохраняется.
Выберем начало О оси X на противоположном начальному положению человека конце лодки, а ось X направим вдоль лодки в направлении человека. Положение ЦМ системы человек-лодка при t=0 в выбранной СО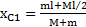 
, а после его перехода на другой конец лодки 
. Из условия 
опять получим 
. Разделив обе части этого равенства на время t движения человека по лодке и обозначая 
и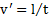 
придем к прежнему выражению для скорости лодки относительно берега.
Ответ: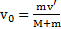 
, .
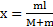Пример 2. На параллелепипед с массой M, находящимся на горизонтальной гладкой поверхности, лежит тело массой m. Телу сообщают горизонтальную начальную скорость 
. Найти ускорение, с которым будет двигаться параллелепипед после толчка, и ускорение движения тела относительно параллелепипеда. Какой путь и за какое время пройдет тело при его движении по поверхности параллелепипеда до остановки? На какое расстояние сместится параллелепипед за это время? Какова начальная скорость параллелепипеда после толчка? Коэффициент трения между телом и параллелепипедом равен μ. Трение между параллелепипедом и горизонтальной поверхностью отсутствует.
Дано: 
. Найти: 
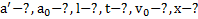
Решение: Для решения задачи выберем две СО: неподвижную XOY, связанную с горизонтальной плоскостью, и движущуюся – 
, связанную с параллелепипедом. Оси X и 
направим параллельно горизонтальной плоскости (рис.37) в направлении ускорений параллелепипеда 
и тела 
Рис.37
После толчка тела между телом и параллелепипедом возникнут силы трения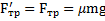 
и параллелепипед начнет двигаться с ускорением , а на тело подействует сила инерции 
.
Из второго закона Ньютона для параллелепипеда (рис.37) 
найдем его ускорениев неподвижной СО 
, а из второго закона Ньютона для тела 
его ускорение в движущейся СО 
. Ускорения тел связаны соотношением 
.
Путь, пройденный телом и время его движения по поверхности параллелепипеда до остановки равны
, 
.
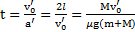Система двух тел является замкнутой и, в частности, замкнутой в направлении осиX. Поэтому в системе имеет место закон сохранения импульса, который в начальный момент времени был равен нулю. С учетом, что в неподвижной СО скорость тела равна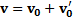 
закон сохранения импульса в рассматриваемой системе двух тел будет в момент времени t=0 в неподвижной СО иметь вид
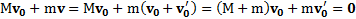
Откуда скорость параллелепипеда после толчка тела равна 
. В скалярной форме 
. В произвольный момент времени связь между скоростями тел будет такой же 
.
Смещение параллелепипеда за время движения тела по его поверхности найдем из закона сохранения положения ЦМ системы. Для этого выберем начало О СО XOY в точке конечного положения тела, а ось X направим в сторону его начального положения (рис.36). Обозначая 
положение ЦМ параллелепипеда, получим для начального и конечного положений ЦМ системы: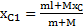 
, 
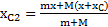. Из условия приходим к уравнению 
, из которого находим смещение параллелепипеда 
.
Уравнения движения тел в неподвижной и движущейся СО в проекциях на направления скоростей их движения и предположения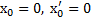 
имеют вид
; 
.
Ответ: , 
, 
, 
, , 
.
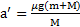Пример 3. Решить предыдущую задачу в предположении, что начальная скорость 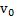была сообщена параллелепипеду (рис.37).
Дано: 
. Найти: 
Решение: Ускорения тел, входящие во второй закон Ньютона, не зависят от их начальной скорости, и они после толчка будут двигаться с теми же ускорениями 
, 
.
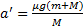Закон сохранения импульса в системе будет иметь такой же вид, как и в предыдущем примере. Решая полученное уравнение относительно параметра , получим для начальной скорости тела 
. Тогда путь и время движения тела по поверхности параллелепипеда будут равны (конечные выражения отличаются для полученных в предыдущем примере)
, 
.
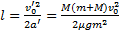Закон сохранения положения ЦМ системы не изменится и из него получим для смещения параллелепипеда за время движения тела по нему 
.
Ответ: 
, , 
, 
, , 
.
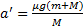Столкновения тел
Различают следующие виды соударений тел: абсолютно неупругое, частично-упругое и абсолютно упругое. Если процесс столкновения быстрый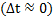 
, то имеет место закон сохранения импульса в системе сталкивающихся тел.
Абсолютно неупругое столкновение тел. При этом виде столкновения тела слипаются и после столкновения движутся вместе(рис.38).
Рис. 38
Любое столкновение тел описывается законом сохранения импульса и энергии. В данном случае, обозначив импульсы тел до и после столкновения 
, 
, 
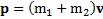и Q – выделившееся при ударе тепло, получим
.
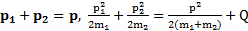Возведя первое равенство в квадрат, найдем квадрат импульса тел после столкновения, а из второго – выделившееся при ударе тепло
, 
,
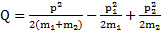где 
– угол между векторами импульсов тел до их столкновения.
При прямом центральном ударе скорость тел после столкновения 
, а выделившееся при ударе тепло
,
где 
и 
– проекции скоростей тел 
и 
на направление их движения и имеют знак 
.
Частично упругое столкновение тел. Ограничимся случаем лобового столкновения тел. При этом виде удара тела не слипаются, но после столкновения у них имеется остаточная деформация (вмятины) и выделяется при ударе тепло 
. Законы сохранения импульса в проекциях на направление движения тел и энергии в этом случае будут иметь вид
,
где 
и 
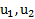– скорости тел до и после их столкновения.
Абсолютно упругое столкновение тел. При этом виде столкновения тела после столкновения восстанавливают свою форму и остаточная деформация у них отсутствует, поэтому выделившееся при ударе тепло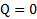 
Рис.39
Система уравнений, описывающая удар (рис.39), будет иметь вид
, 
.
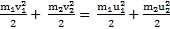Эту систему уравнений можно свести к линейной. Для этого перенесем члены с одинаковыми индексами в одну часть равенства. Получим
, 
.
Разделив второе уравнение на первое и добавив к полученному уравнению закон сохранения импульса, придем к линейной системе уравнений
, ,
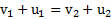решая которую, получим
, 
.
В этих уравнениях и 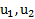– это проекции скоростей тел на выбранное направление оси проецирования X и имеют знак . Если при расчетах будет получено 
, это означает, что скорость тела 
после столкновения тел направлена противоположно выбранному направлению оси X.