Установившаяся концентрация носителей заряда является результатом динамического равновесия между процессами генерации и рекомбинации. Эти процессы можно схематически представить в виде:
,
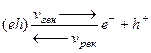где (eh) отображает связанное состояние электрона, e- и h+ - свободный электрон и дырка.
Скорость термогенерации зависит от типа полупроводника и температуры:
vген=g0(T)
Скорость рекомбинации пропорциональна произведению концентраций носителей:
vрек=r0 np
В равновесии vген= vрек, отсюда
np=ni2= g0 /r0
Среднее время жизни равновесных носителей равно отношению концентрации этих носителей к скорости рекомбинации. Таким образом,
tn=n/vрек= 1/(r0 p), tp=p/vрек= 1/(r0 n)
Отсюда следует, что время жизни неосновных носителей на несколько порядков меньше времени жизни основных. Например,
(tp) n= 1/(r0 Nd)<< (tn) n= 1/(r0 pn) = Nd /(r0 ni2)
Неравновесная концентрация носителей.
Неравновесная концентрация носителей в полупроводнике может быть создана при различных энергетических воздействиях (облучение светом, импульсный нагрев, инжекция из соседних областей и др.). Неравновесные концентрации можно записать в виде
n=n0+ D n,
p=p0+ D p,
где D n иD p – отклонение концентраций от равновесных значений n0 и p0.
Объем полупроводника сохраняет электронейтральность, поэтому всегда
D n= D p
После прекращения воздействия избыточные носители рекомбинируют, и концентрации возвращаются к исходным значениям. Скорость рекомбинации пропорциональна отклонению:
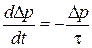, и 
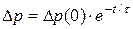(1.11)
где t - время жизни неравновесных носителей, D p (0) – начальное отклонение.
Когда приращение концентрации значительно меньше концентрации основных носителей, значение t близко к времени жизни неосновных носителей.
|
|
Механизмы рекомбинации.
Различают непосредственную рекомбинацию и рекомбинацию на примесных центрах (ловушках).
При непосредственной рекомбинации электрон из зоны проводимости переходит в валентную зону, заполняя вакантный уровень, т.е. уничтожая дырку. При этом должна выделиться энергия, равная ширине запрещенной зоны D W. Энергия может выделяться либо в виде фотона (излучательная рекомбинация), либо в виде фонона (безызлучательная рекомбинация). В большинстве полупроводниках, в частности, в кремнии и германии, вероятность излучательной рекомбинации на несколько порядков меньше, чем безызлучательной. Однако вероятность безызлучательной рекомбинации также мала, поскольку сравнительно большая энергия редко может быть передана одному фонону, а ее распределение между двумя фононами маловероятно. Поэтому непосредственная рекомбинация не является главным механизмом рекомбинации в полупроводниках.
Главную роль играет рекомбинация на примесных центрах, когда атомы примеси, образуют глубокие уровни вблизи середины запрещенной зоны, которые называются ловушками. В этом случае рекомбинация протекает в два этапа – сначала электрон переходит из зоны проводимости на уровень ловушки и находится там некоторое время, а затем переходит в валентную зону. На каждом этапе выделяется энергия, примерно вдвое меньшая, чем при непосредственной рекомбинации, что резко повышает вероятность передачи энергии фонону. Столкновение с фононом может также перевести электрон из валентной зоны на уровень ловушки и на следующем этапе с этого уровня – в зону проводимости, что соответствует двухступенчатой генерации. В присутствии ловушек процессы генерации-рекомбинации идут значительно интенсивнее и время жизни носителей оказывается значительно меньше.
|
|
На рис.1.3 показаны двухступенчатые процессы. Электрон может перейти на уровень ловушки из зоны проводимости и затем соединиться с дыркой – рекомбинация (а) или из валентной зоны (оставляя дырку) и затем в зону проводимости – генерация (б). Ловушка может также захватить дырку, а затем на этот уровень может перейти свободный электрон (в) – рекомбинация. Наконец, атом примеси может отдать свой электрон в зону проводимости, а затем захватить электрон из валентной зоны (г) – генерация. Штриховые стрелки показывают, что захваченный носитель может также вернуться обратно.
Роль ловушек могут играть не только примесные атомы, но и различные дефекты кристаллической решетки. Из-за нарушения кристаллической решетки у поверхности полупроводника образуется множество дополнительных уровней в запрещенной зоне, которые и служат центрами рекомбинации. Поэтому время жизни носителей у поверхности оказывается значительно меньше, чем в объеме, и, если в объеме создана неравновесная концентрация, возникает поток носителей к поверхности, где они рекомбинируют.
ЗАКОНЫДВИЖЕНИЯ НОСИТЕЛЕЙ В ПОЛУПРОВОДНИКАХ
Согласно квантовой теории для описания движения свободных носителей в кристалле можно использовать понятие эффективной массы электрона mn и дырки mp. Эффективная масса не совпадает с массой свободного электрона mo в вакууме, обычно mn < mp. Например, в кремнии mn= 0,33 m0, mp= 0,55 m0. Импульс электрона не сохраняется при движении в периодическом электрическом поле кристалла и вместо него вводится понятие квазиимпульса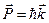 
, где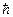 
– постоянная Планка, 
– волновой вектор. Квазиимпульс подчиняется закону сохранения. В отличие от электронов в вакууме связь энергии и квазиимпульса электронов в кристалле зависит от кристаллографического направления вследствие анизотропии кристалла.
|
|
В идеальном кристалле свободные носители движутся без соударений и при отсутствии внешних сил их квазиимпульс постоянен. В реальном кристалле всегда присутствуют дефекты кристаллической решетки, на которых происходит рассеяние носителей, т.е. изменение направления и скорости их движения при взаимодействии с дефектом. Важнейшими дефектами являются ионы донорных и акцепторных примесей, поскольку практически в любом приборе применяются примесные полупроводники. Идеальность решетки нарушается также за счет тепловых колебаний атомов, которые вызывают рассеяние, называемое фононным, так как оно сопровождается возбуждением или поглощением фононов.
Тепловое движение.
Свободные носители в полупроводниках можно рассматривать как электронный или дырочный газ, заполняющий объем кристалла, в котором частицы находятся в непрерывном хаотическом тепловом движении. Средняя скорость теплового движения определяется по известной формуле 
, где m – эффективная масса частицы. Время tпр и длина lпр=vTlпр свободного пробега определяется процессами рассеяния, т.е. зависит от концентрации центров рассеяния и температуры
При хаотическом движении направления скоростей носителей равновероятны и электрический ток равен нулю.
Дрейфовое движение.
Если в полупроводнике создано электрическое поле, носители ускоряются этим поле на пути свободного пробега. Приобретенная скорость теряется при рассеянии, затем носители снова ускоряются до следующего столкновения. В результате хаотическое движение носителей приобретает составляющую, направленную вдоль вектора напряженности поля. Направленное движение носителей под действием электрического поля называется дрейфом (дрейфовым движением). Скорость направленного движения, усредненная по всем носителям одного знака, называется скоростью дрейфа vдр. Скорость дрейфа пропорциональна напряженности электрического поля E:
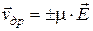(1.12)
Коэффициент пропорциональности m называется подвижностью, см2/(В×с). Это средняя скорость, которую приобретает электрон или дырка в электрическом поле с напряженностью 1 В/см. Здесь знак «+» относится к дыркам, «–» – к электронам. Здесь и далее будем рассматривать одномерный случай и опускать обозначение векторной величины.
Направленное движение носителей заряда – это электрический ток. Плотности электронной и дырочной составляющих дрейфового тока равны произведению плотности соответствующих зарядов на скорость дрейфа:
(jn) др= – en (vn) др=en m nE (1.13 а)
(jp)др= ep(vp)др =ep m pE, (1.13 б)
где mn и mp – подвижности электронов и дырок, e – элементарный заряд. Плотность дрейфового тока равна
jдр=(jn) др + (jp) др =e (n m n+ p m p ) E (1.14)
Здесь коэффициент пропорциональности перед E – удельная электропроводность s:
s= e (n m n+ p m p ) (1.15)
Диффузия.
При неравномерном распределении частиц в объеме возникает направленное движение, стремящееся выровнять концентрацию, которое называется диффузией. Скорость диффузии пропорционально градиенту концентрации с обратным знаком. В случае заряженных частиц это приводит к появлению диффузионных токов:
(jn) дф=eDn (dn/dx) и (jp) дф=- eDp (dp/dx), (1.16)
где Dn и Dp – коэффициенты диффузии электронов и дырок, см2/с. Ток дырок направлен против градиента концентрации вследствие их положительного заряда, электронный ток противоположен направлению их движения.
Электронный и дырочный токи включают обе составляющие (1.13) и (1.16):
jn =en m nE + eDn (dn/dx), (1.17)
jp=ep m pE- eDp (dp/dx). (1.18)
Подвижность и коэффициент диффузии связаны соотношением Эйнштейна:
D= j T× m, (1.19)
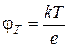(1.20)
Коэффициент φ Т называется температурным потенциалом.