Для охлаждения бензола в межтрубное пространство кожухотрубчатого теплообменника с диаметром кожуха D = 800 мм, диаметром труб d×δ = 12×2 мм и их числом 490 шт. подаётся вода со средней температурой 30ºС. Скорость воды в межтрубном пространстве должна быть 0,3 м/с. Необходимо определить расход воды в м3/час и режим её движения.
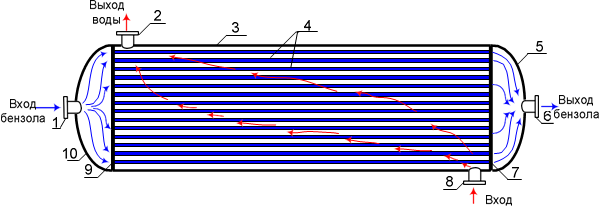
Рис. 2 к задаче 3. Вода подаётся в межтрубное пространство.
Решение.
Решение этой задачи основано на уравнении объёмного расхода
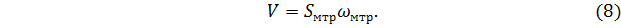
Но Sмтр – это площадь сечения межтрубного пространства. Если рассечь корпус нашего теплообменника плоскостью, то в сечении мы увидим такую фигуру
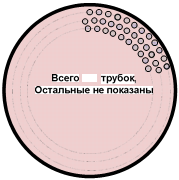
Рис. 3 к задаче 3. Сечение межтрубного пространства.
Площадь сечения межтрубного пространства будет равна
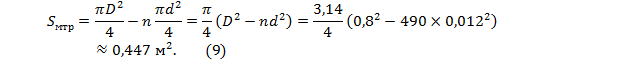
Теперь в формулу подставляем наружный, а не внутренний диаметр трубок. Внутри трубок движется бензол.
Теперь находим объёмный расход воды, которая движется в межтрубном пространстве со скоростью 0,3 м/с.
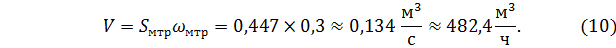
Следует отметить, что на производстве принято расход воды измерять именно в кубических метрах в час, а не в секунду.
Теперь определим режим движения воды в межтрубном пространстве. Для этого надо вычислить значение критерия Рейнольдса. Для трубы в формуле для критерия Рейнольдса участвует её внутренний диаметр. У нашего профиля нет диаметра (рис. 3). В таких случаях в расчётах используется эквивалентный диаметр, т.е. для потоков некруглого сечения делается попытка сравнить их с потоком круглого сечения, с трубой. Классическая расчётная формула имеет вид
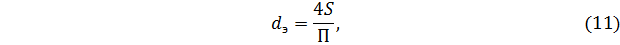
где S – площадь сечения потока, в нашем случае это будет Sмтр, П – смоченный периметр, т.е. те длины, которые смачивает жидкость. В нашем примере это будут длина окружности кожуха плюс сумма всех длин окружностей трубок. Запишем формулу
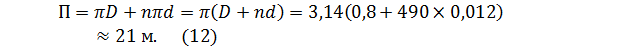
Подставим полученное значение в формулу (11) и получим
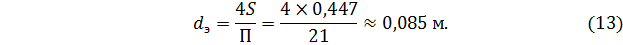
Т.е. то сечение, по которому течёт вода, эквивалентно трубе с внутренним диаметром 85 мм.
Теперь вычислим значение критерия Рейнольдса для воды
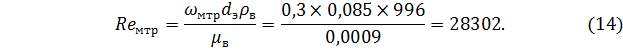
Следовательно, режим движения воды в межтрубном пространстве нашего аппарата будет турбулентным.
Ответ: объёмный расход воды 482,4 м3/ч, режим её движения – турбулентный.
Задача 3
На трубопроводе имеется переход с диаметра 70 мм на диаметр 130 мм (диаметры внутренние). По трубопроводу движется вода, имеющая температуру 20ºС. Её скорость в узком сечении 3,1 м/с. Определить:
1. объёмный и массовый расходы воды;
2. скорость воды в широком сечении;
3. режимы течения в узком и широком сечениях.
Решение.
Сделаем эскиз для этой задачи.
| Рис. 4 |
Проведём на нашем эскизе два сечения, проходящие через трубу диаметром 70 мм и через трубу диаметром 130 мм. Обозначим их 1-1 и 2-2.
Уравнение материального баланса (уравнение неразрывности потока) для наших выбранных сечений можно записать так
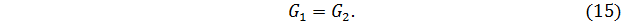
Учитывая, что G = V × ρ, можно записать уравнение (15) так
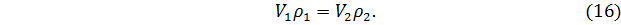
Распишем объёмный расход V по уравнению (1)
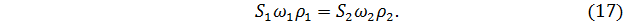
Так как наши потоки – трубы, т.е. имеют круглое сечение, то уравнение (17) можно записать так
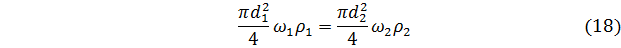
или после сокращения
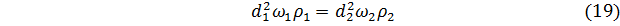
В общем случае сокращать плотность ρ сразу нельзя, т.к. не сказано, что в разных сечениях она одинакова.
Можем допустить, что вода при переходе из сечения 1-1 в сечение 2-2 не изменяет свою плотность, ρ1 = ρ2. Тогда из уравнения (19) получим
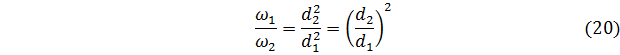
Т.е. получим, что скорость потока в трубе обратно пропорциональна квадрату её диаметра. Следовательно, при увеличении диаметра в 2 раза скорость уменьшается в 4 раза. А если диаметр уменьшился в 3 раза, то скорость возрастёт в 9 раз.
Определим объёмный и массовый расходы воды. Для нахождения объёмного расхода воспользуемся уравнением (1)
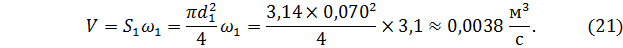
Массовый расход воды будет равен
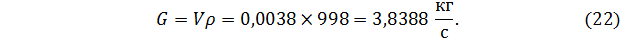
Скорость воды в широком сечении 2-2 найдём из уравнения (20)
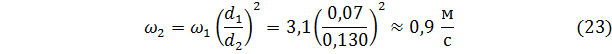
Критерий Рейнольдса для узкого сечения 1-1
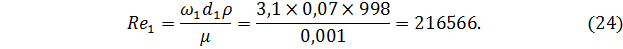
Критерий Рейнольдса для сечения 2-2
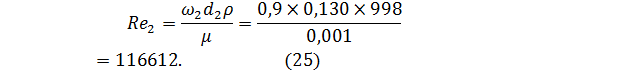
Ответ: объёмный расход воды 0,0038 м3/с, массовый расход 3,8388 кг/с, скорость воды в широком сечении 0,9 м/с, режим движения воды в обоих сечениях – турбулентный.
Задача 4
Труба диаметром 110×4 мм переходит в трубу диаметром 90×4 мм, после чего поднимается вверх на 15 м. В нижнем и верхнем сечениях трубы установлены манометры. Нижний манометр показывает давление Р1 = 5 кГс/см2. По трубопроводу перекачивается вода с расходом 55 м3/ч и температурой 40ºС. Определить показания верхнего манометра. Наличием сил вязкости пренебречь.
Решение.
| 35×2 мм |
| 55×2 мм |
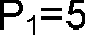
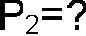
Начнём решение с эскиза. Это наша труба, которая сначала «худеет», а потом резко поднимается на 15 м. Нам надо определить, какое давление покажет манометр Р2.
Запишем уравнение Бернулли для нижнего 1 и верхнего 2 сечений:
| Рис. 9 к задаче 7 |
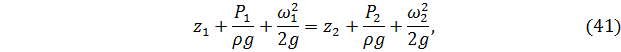
где z – геометрический напор,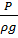 
– статический напор, 
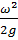– скоростной напор. Все они измеряются в метрах.
Нам нужно найти Р2. Для этого необходимо сначала вычислить скорости воды в широкой и узкой трубах.
Скорость воды в широкой трубе
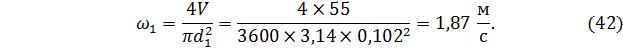
Скорость воды в узкой трубе можно найти точно также, а можно как мы её находили в задаче 4 (уравнение (23)). Посчитаем и так, и так для проверки совпадения.
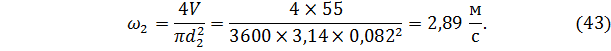
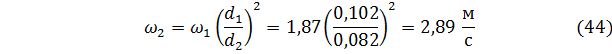
Теперь выразим из уравнения Бернулли дробь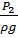 
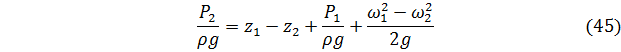
Разность z1 - z2 ‒ это подъём нашей трубы на 15 м. Но в уравнение (45) эту величину надо подставлять со знаком минус, т.к. z2 больше z1 именно на 4 м.
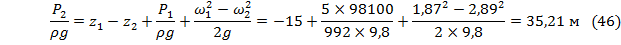
В уравнении (46) для давления Р сделан переход из кГс/см2 в паскали (Па) путём умножения на переводной коэффициент 98100, т.к. все расчёты надо делать строго в системе СИ.
Осталось перейти из напора в давление
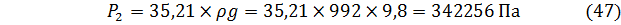
После перевода в кГс/см2 получим
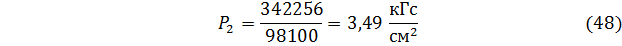
Ответ: верхний манометр покажет давление 3,4 кГс/см2.
Задача 5
По трубопроводу длиной 15 км и диаметром 190×4 мм перекачивается бензол с расходом 63 т/ч при средней температуре 20°С. Стенки трубопровода гладкие. Манометр, установленный в начале, показывает давление 4 ат. Определить показание манометра, установленного в конце трубопровода.
Решение.
| Рис. 10 к задаче 8 |
| 135×3 |
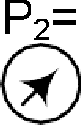
Сделаем эскиз для этой задачи. Решение этой задачи основано на знании формул Дарси-Вейсбаха и Блазиуса.
Вычислим скорость бензола в трубе.
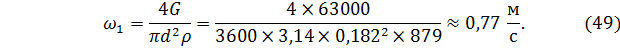
Найдём значение критерия Рейнольдса
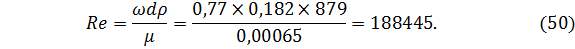
По формуле Блазиуса определим значение коэффициента трения
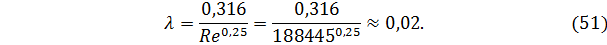
По уравнению Дарси-Вейсбаха определим потерю давления
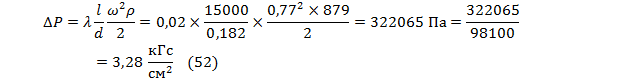
Итак, потеря давления составила 3,28 кГс/см2, второй манометр покажет 0,72 кГс/см2.
Ответ: второй манометр покажет 0,72 кГс/см2.