Вариант 1.
| Скалярная теория дифракции работает даже для объектов, сравнимых с длиной волны света. | да | нет |
Скалярная теория дифракции дает очень хорошие результаты, подтвержденные экспериментами, но при следующих условиях:
1) отверстия в экранах велики, по сравнению с длиной волны l;
2) дифрагированные волны наблюдаются не слишком близко от экрана.
| Уравнение Гельмгольца имеет частное решение в виде суперпозиции Бесселевых функций. | да | нет |
Известно, что волновое уравнение Гельмгольца
имеет частное решение в виде бесселевых мод:
| Параксиальное приближение верно в случае, когда размеры поперечных координат сравнимы с размером продольной координаты | да | нет |
Параксиальное приближение верно в случае, когда размеры поперечных координат много меньше (<<) размеров продольной координаты. Сферическую волну:
в точке (x,y,z), достаточно близкой к оси z, но далекой от начала координат (см. Рис. 6).
Рис. 6
В этом случае можно считать, что 
(условие параксиальности).
| Многопорядковый ДОЭ работает как пространственный фильтр, согласованный с некоторым набором ортогональных функций. | да | нет |
Предлагается метод композиций для расчета широкого класса ДОЭ. При этом функция комплексного пропускания ДОЭ t (x) представляется в виде конечной линейной комбинации ортогональных функций: 
, (1.65)
где j (x) - фаза ДОЭ, A (x) - амплитуда ДОЭ (для фазовых ДОЭ связывается с амплитудой освещающего пучка), Y n (x) – набор ортонормированных функций, W – множество индексов n с ненулевыми коэффициентами, C n – комплексные коэффициенты суммы (1.65), которые вычисляются по формуле: 
, (1.66)
Для многоканальных ДОЭ, формирующих световые распределения в нескольких порядках дифракции, к выбранным базисным функциям добавляют пространственные несущие /244, 308/. Такие многоканальные ДОЭ могут использоваться как для одновременного формирования нескольких световых пучков, распространяющихся под различными углами к оптической оси /49*, 308/, так и в качестве пространственных фильтров для вычисления коэффициентов разложения светового поля по некоторому ортогональному базису.
| Функции Бесселя являются модами свободного пространства. | да | нет |
Инвариантность к оператору распространения, или, преобразованию Френеля, демонстрируют световые моды в своих средах: Бесселевы моды - в свободном пространстве, моды Гаусса-Лагерра и Гаусса-Эрмита - в оптической среде с параболическим показателем преломления. Гауссовы моды также можно считать модами свободного пространства с точностью до масштаба. Однако, свойством инвариантности к оператору распространения обладают каждая мода в отдельности. Произвольная композиция световых мод, в общем случае, таким свойством не обладает.
| Кодирование амплитудно-фазового распределения в чисто амплитудное или число фазовое используется в оптике для сжатия информации. | да | нет |
| Теорема Котельникова позволяет получить связь между дискретностью в объектной и частной плоскостях для преобразования Фурье. | да | нет |
| Моды Гаусса – Эрмита инвариантны к повороту. | да | нет |
Свойством инвариантности к повороту обладают все радиально-симметричные световые поля. Среди модовых функций к этому типу относятся Бесселевы функции нулевого порядка и необобщенные функции Гаусса-Лагерра, а также любые их линейные комбинации.
Моды Гаусса-Эрмита не обладают свойством инвариантности к повороту, но они инвариантны к преобразованию Фурье, Френеля.
| Сохранение ортогональности при распространении является основным свойством моды. | да | нет |
Мода обладает следующими основными свойствами:
1) инвариантность к оператору распространения в своей среде,
2) сохранение ортогональности при распространении,
3) меньшие потери энергии для мод с меньшими индексами,
4) наилучшая среднеквадратичная аппроксимация полей, распространяющихся в данной среде.
| Многомодовый световой пучок обладает теми же свойствами, что и одномерный. | да | нет |
Произвольная композиция световых мод, в общем случае, свойством инвариантности к оператору распространения не обладает.
Свойством инвариантности к оператору распространения обладают каждая мода в отдельности, в том числе и одномодовый (одномерный пучок).
| Введение параметров адаптации и регуляризации позволяет снизить уровень стагнации в итеративных алгоритмах. | да | нет |
Модификация адаптивно-регуляризационного алгоритма для метода композиций выглядит следующим образом:
(1.115)
где b - параметр регуляризации, a >0 - параметр адаптации алгоритма или константа релаксации.
В общем виде адаптивно-регуляризационный алгоритм (1.115) позволяет регулировать скорость сходимости рассчитанных коэффициентов к заданным и преодолевать стагнацию за счет дополнительно введенных в рассмотрение ненулевых коэффициентов, регулируя их энергетический вклад.
| Кодирование для бинарных носителей требует большего количества отсчетов, чем для многоградационных | да | нет |
при бинарной среде при кодировании 1-го отсчета необх много отсчетов. бин. изготавливать сложнее(коммент был дан на лекции, списано у Гули Юношевой =))
| Амплитудные оптические элементы являются более энергетически выгодными, чем фазовые. | да | нет |
(0-1)Наибольший интерес с точки зрения энергетической эффективности представляют собой фазовые ДОЭ:
,
Фазовые ДОЭ осуществляют требуемые преобразования волновых полей теоретически без потери световой энергии (практическая дифракционная эффективность 60-95%). Действие фазового ДОЭ в приближении тонкой оптики сводится к определенному набегу фазы падающего излучения в каждой точке области ДОЭ. Затем, после прохождения некоторого расстояния, фазовые изменения проявляются в изменениях амплитуды падающего света.
| Энергетическая эффективность дифракционного оптического элемента и точность формирования заданного распределения являются конкурирующими параметрами. | да | нет |
(0-2)Качество расчета и изготовления ДОЭ характеризуется степенью отличия сформированного распределения света от заданного и величиной световой энергии, идущей на формирование этого распределения. Для задач обработки информации, в которых требуется высокая точность формирования волновых фронтов или распределений интенсивности, основной характеристикой качества ДОЭ является ошибка отклонения. А для задач обработки материалов мощным лазерным излучением требуется высокая степень концентрации энергии в области заданного изображения. Для таких задач требуются фазовые ДОЭ, обладающие высокой энергетической эффективностью.
С целью достижения оптимальных соотношений конкурирующих параметров: точности и эффективности формирования светового поля, следует применять методы кодирования ДОЭ, обеспечивающие повышенную дифракционная эффективность.
| Один и тот же ДОЭ можно использовать для излучения с различными длинами волн. | да | нет |
(0-2)Высота микрорельефа, создаваемого на прозрачной или отражающей пластинке определяется по формуле 
, (3)
где l – длина волны освещающего ДОЭ источника, n – коэффициент преломления материала пластинки.
Максимальная высота рельефа составляет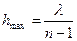 
(4)
и имеет порядок длины волны (например, для стекла n= 1,5 и hmax =2 l).
Вариант 2.
| Уравнение Гельмгольца описывает параксиальное приближение в оптике. | да | нет |
уравнение Гельмгольца: 
(1.3)
описывающее распространение пространственной части. 
называется комплексной амплитудой.
| В рамках скалярной теории поле за непрозрачным экраном полагается равным нулю.пересмотреть | да | нет |
Ясно, что введение диафрагмы (непрозрачного экрана с отверстием заданной формы) точно заданных размеров, как и формирование освещающего гауссового пучка с точно заданными параметрами, представляют практическую сложность /103*/.
Для ослабления жесткой зависимости от формы и размеров диафрагмы и освещающего пучка в данной работе предлагается ввести "мягкую" диафрагму, представляющую собой дополнительные скачки фазы ДОЭ приблизительно там, где должна проходить граница диафрагмы.
Таким образом, во входной плоскости будет формироваться световое поле вида:
, (2.12)
(2.13)
где W(c,d) - форма "мягкой" диафрагмы.
| Волновой фронт определяется по функции фазы. | да | нет |
Волновым фронтом называются поверхности равной фазы:
, q - целое.
Плоская волна имеет следующую комплексную амплитуду:
. (1.4)
где A - комплексная константа, называемая комплексной оболочкой, 
- волновой вектор.
Так как фаза 
, то волновой фронт определяется из уравнения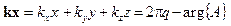 
, q - целое, и будет представлять собой параллельные плоскости, перпендикулярные волновому вектору k (поэтому и называется плоская волна).
| Чем больше степеней свободы, тем хуже сходится итеративный алгоритм. | да | нет |
Разработанные итеративные алгоритмы работают тем лучше, чем больше имеется степеней свободы, которыми являются фазы весовых коэффициентов в композиции. В случае малого числа свободных параметров в композиции, в частности, при формировании одномодовых пучков (одно слагаемое), итерационные методы приводят к стагнации через 1–2 итерации.
| Световое поле в дальней зоне дифракции рассматривается как суперпозиция плоских волн. | да | нет |
| В зоне дифракции Френеля невозможно использование интеграла Кирхгофа в параксиальном приближении. | да | нет |
интеграл Кирхгофа имеет простую физическую интерпретацию в соответствии с принципом Гюйгенса-Френеля: поле в точке представляет собой суперпозицию сферических волн, распространяющихся из каждой точки апертуры системы.
| Возникновение эффекта стагнации указывает на то, что итеративный алгоритм достиг локального максимума функционала. | да | нет |
Эффект стагнации показывает, что алгоритм достигает локального минимума функционала (2.11) и в этом смысле он является квазиоптимальным. Чтобы увеличить скорость сходимости процедуры и частично избежать эффекта стагнации, используется целый ряд адаптивных алгоритмов, в которых вводятся некоторые параметры, контролирующие скорость сходимости. Поэтому иногда эти алгоритмы называют параметрическими.
| Любое световое поле можно представить в виде конечной суммы модовых функций. | да | нет |
| Многомодовый лазерный пучок всегда сохраняет свою структуру при распространении | да | нет |
Свойством инвариантности к оператору распространения обладают каждая мода в отдельности. Произвольная композиция световых мод, в общем случае, таким свойством не обладает.
| При расчете дифракционного оптического элемента, формирующего одномодовый пучок, лучше использовать итерационные алгоритмы. | да | нет |
Итеративные алгоритмы работают тем лучше, чем больше имеется степеней свободы, которыми являются фазы весовых коэффициентов в композиции. В случае малого числа свободных параметров в композиции, в частности, при формировании одномодовых пучков (одно слагаемое), итерационные методы приводят к стагнации через 1–2 итерации. При этом результат близок к методу кодирования киноформов: высокая дифракционная эффективность достигается за счет понижения точности формируемого пучка. Также затрудненно применение итеративных алгоритмов при формировании в сечении пучка заданного изображения. В этом случае амплитуды и фазы коэффициентов также заданы и свободные параметры отсутствуют. В этих двух случаях необходимо применять методы кодирования амплитудно-фазовой функции в чисто фазовую.
| Метод кодирования Лезема для киноформов является итерационным методом. | да | нет |
Киноформ (Метод Лезема). – НЕ итерационный метод (численный расчет)
Киноформ представляет из себя тонкую фазовую пластинку с постоянным амплитудным пропусканием и фазовым пропусканием, определяемым фазой j (u,v) функции комплексного пропускания.
В каждом отсчете комплексную функцию A exp(i j) заменяют на exp(i j), т.е. заменяют везде амплитуду на единичное значение.
Хотя потеря амплитудной информации приводит к ошибкам при восстановлении комплексной амплитуды самого объекта (20-30%), но такие элементы энергетически выгодны - более половины энергии освещающего пучка идет на формирование объекта.
| Метод частичного кодирования позволяет варьировать соотношение таких характеристик оптического элемента как энергетическая эффективность и точность формирования заданного распределения. | да | нет |
Метод частичного кодирования является универсальным для различных задач, т.к. позволяет варьировать параметры "точность" и "эффективность" в широких пределах и достигать наилучших в конкретном случае соотношений. Это достигается за счет введения параметра степени кодирования, в качестве которого выступает пороговый уровень амплитуды, ниже которого амплитуда кодируется в фазу, а выше которого заменяется на постоянную величину.
| Параметр адаптации в итеративных алгоритмах регулирует соотношение энергии в полезной области и остальной области. | да | нет |
Модификация адаптивно-регуляризационного алгоритма для метода композиций выглядит следующим образом:
(1.115)
где b - параметр регуляризации, a >0 - параметр адаптации алгоритма или константа релаксации.
В общем виде адаптивно-регуляризационный алгоритм (1.115) позволяет регулировать скорость сходимости рассчитанных коэффициентов к заданным и преодолевать стагнацию за счет дополнительно введенных в рассмотрение ненулевых коэффициентов, регулируя их энергетический вклад.
| Основным подходом при кодировании методами цифровой голографии является введение дополнительных дифракционных порядков. | да | нет |
Кодирование функции пропускания с введением вспомогательных элементов может осуществляться аналитически (например, введением в фазу или амплитуду несущей частоты, что приводит к формированию вспомогательных дифракционных порядков) или в ходе итерационного процесса.
Но: Общим недостатком методов Ломана, Ли и Бэркхардта является низкая энергетическая эффективность, что вызвано амплитудным характером голограммы и возникновением высших дифракционных порядков вследствие неявного введения несущей.
| Фазу светового поля можно напрямую зарегистрировать каким-нибудь фоточувствительным устройством. | да | нет |
| 3+ | Нулевое значение интенсивности в центре винтовых пучков возникает из-за неопределенности фазы хз что | да | нет |
на практике приходится иметь дело с градиентными волокнами, реальный профиль которых значительно отличается от идеального параболического. Как правило, имеет место резкий провал значения показателя преломления в центре сердцевины волокна, что объясняется спецификой используемой технологии изготовления градиентных волокон. Уменьшить влияние технологических погрешностей изготовления волокон можно, выбирая для передачи одного канала связи группу мод ГЛ, имеющих нулевую интенсивность в центре, связанную с фазовой особенностью обобщенных мод ГЛ exp(imf), m ¹0.
| 7+ | Сфероидальные волновые функции являются модами градиентных оптических волокон | да | нет |
| 14+ | Гауссовы моды являются частным решением уравнения Гельмгольца | да | нет |
Частным решением уравнения Гельмгольца являются плоские и сферические волны, а также моды Бесселя
Вариант 3.
| Применение интеграла Кирхгофа возможно только в дальней зоне дифракции. | да | нет |
Интеграл Кирхгоффа применяется к сферическим волнам, которые существуют именно в ближней зоне дифракции. 
| При параксиальном приближении рассматриваются области в поперечной плоскости, близкие к оптической оси. | да | нет |
Параксиальное, оно же параболическое, приближение предполагает наличие волнового фронта такого, что его возможно аппроксимировать параболой, а это возможно лишь в поперечной плоскости направления распространения волны на небольшом расстоянии от оптической оси.
| Дифракционные оптические элементы хорошо работают только в случае когерентного монохроматического излучения. | да | нет |
Свет считается монохроматическим и когерентным, если его можно описать некоторой комплексной функцией, удовлетворяющей уравнению Гельмгольца.
Оптический элемент расчитывается для монохроматического когерентного пучка.
Полихроматический пучок будет по-разному преломляться, а если пучок некогерентный, то вообще дифракции не получим.
| Киноформ – это амплитудный оптический элемент | да | нет |
Киноформ представляет из себя тонкую фазовую пластинку с постоянным амплитудным пропусканием и фазовым пропусканием, определяемым фазой j (u,v) функции комплексного пропускания.
| В зоне дифракции Фраунгофера распространение света можно описывать с помощью преобразования Фурье. | да | нет |
В зоне дифракции Фраунгофера (при удалении по оси z на расстояние 
) волны практически плоские, можно использовать преобразование Фурье.
| При использовании последовательно нескольких итеративных алгоритмов лучше начинать с тех, ограничения в которых наиболее жесткие. | да | нет | |
| Свойством периодического самовоспроизведения при распространении обладают только одномодовые световые пучки. | да | нет |
Периодическое самовоспроизведение – свойство многомодовых световых пучков.
| Базис Карунена-Лоэва является оптимальным при анализе случайных сигналов и изображений. | да | нет |
Функции Карунена-Лоэва:
; 
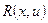- корреляционный оператор.
К оптимальным свойствам относят: 1. Коэффициенты разложения некоррелированы, что благотворно сказывается на качестве распознавания и эффекте кластеризации.
2. Среднеквадратичная ошибка минимальна среди всех ортогональных базисов.
| Гауссовы моды инвариантны к распространению в оптической среде с постоянным показателем преломления. | да | нет |
Инвариантность к оператору распространения, или, преобразованию Френеля, демонстрируют световые моды в своих средах: Бесселевы моды - в свободном пространстве, моды Гаусса-Лагерра и Гаусса-Эрмита - в оптической среде с параболическим показателем преломления. Гауссовы моды также можно считать модами свободного пространства с точностью до масштаба. Однако, свойством инв-ти к оп-ру распространения обладают каждая мода в отдельности. Произвольная композиция световых мод, в общем случае, таким свойством не обладает.
| Высота фазового рельефа ДОЭ, как правило, равна нескольким миллиметрам. | да | нет |
Высота микрорельефа, создаваемого на прозрачной или отражающей пластинке определяется по формуле ,где l – длина волны освещающего ДОЭ источника, n – коэффициент преломления материала пластинки. Максимальная высота рельефа составляет 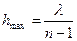Длина световой волны составляет 390 - 760 нанометров. Исходя из этого, для того, чтобы высота микрорельефа была соизмерима с миллиметром, коэффициент преломления вещества, из которого сделан оптический элемент должен быть практически таким же, как и коэффициент преломления окружающей среды, что на практике не используется.
| Накладывая определенные условия на модовый состав светового пучка можно управлять его свойствами самовоспроизведения при распространении в определенной оптической среде. | да | нет |
Многомодовые световые пучки, в отличие от одномодовых, могут проявлять при распространении, кроме свойства инвариантности, такие интересные свойства, как периодическое самовоспроизведение и, в частности, вращение поперечного сечения пучка. Данное явление возникает в результате интерференции нескольких (не менее двух) световых волн, содержащихся в многомодовом пучке. При формировании различных типов многомодовых световых полей желательно иметь простые и удобные условия, накладываемые на модовый состав и обеспечивающие те или иные свойства таких полей.
| Параметр регуляризации в итеративных алгоритмах регулирует распространение в полезной области. | да | нет | |
| Благодаря свойству инвариантности к преобразованию Фурье функции Цернике используются для анализа аберраций волнового фронта светового поля. | да | нет |
Функции Цернике не инвариантны преобразованию Фурье, а инвариантны лишь повороту.
| Фазовую функцию дифракционного оптического элемента, рассчитанную для света одной длины волны, можно использовать для света другой длины волны. | да | нет |
Для монохроматической волны можно записать временную зависимость в виде:
, где ню – длина волны, видимо. Так как эта Байда лежит в основе Всего, то использовать элемент для другой длины волны низя.
| Метод кодирования Ломана характеризуется высокой энергетической эффективностью. | да | нет |
Метод Ломана относится к методам построения амплитудных голограмм, которые характеризуются высокой точностью, но низкой эффективностью.
| 8+ | Наилучшая среднеквадратичная аппроксимация световых полей, распространяющихся в определенной оптичекой среде, достигается при разложении поля по модам этой среды | да | нет |
В теории волноводов существует понятие мод, которые обладают рядом замечательных свойств:
1) инвариантность к оператору распространения в своей среде,
2) сохранение ортогональности при распространении,
3) меньшие потери энергии для мод с меньшими индексами,
4) наилучшая среднеквадратичная аппроксимация полей, распространяющихся в данной среде
| 13+ | Энергетическая эффективность показывает долю энергии, которая попадает от освещающего пучка в заданную область фокусировки | да | нет |
E (u,v) – комплексная амплитуда сформированного поля
e – дифракционная эффективность
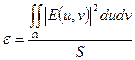, S – энергия освещ. пучка