Лекция 3. Система уравнений МКЭ
Сетка МКЭ
Покроем область  сеткой конечных элементов
сеткой конечных элементов  ,
,  , так чтобы
, так чтобы  .
.
Тогда  . Звёздочка означает, что при интегрировании по границе в сумму входят лишь те конечные элементы
. Звёздочка означает, что при интегрировании по границе в сумму входят лишь те конечные элементы  , границы которых
, границы которых  хотя частично лежат на границе области
хотя частично лежат на границе области  .
.
Рассмотрим отдельный конечный элемент. Например это многоугольник. Пусть он имеет  узлов. Тогда можно ввести базисные функции этого элемента
узлов. Тогда можно ввести базисные функции этого элемента  . Эти функции линейно независимы и нормированы так, что
. Эти функции линейно независимы и нормированы так, что  . Произвольная функция
. Произвольная функция  на элементе
на элементе  может быть представлена разложением по базису
может быть представлена разложением по базису
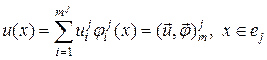 (3.1)
(3.1)
Индекс 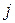 обозначает принадлежность к
обозначает принадлежность к 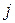 -му элементу. В дальнейшем, если это не приводит к недоразумениям, индекс
-му элементу. В дальнейшем, если это не приводит к недоразумениям, индекс 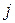 часто будем опускать. Индекс
часто будем опускать. Индекс  используется для локальной нумерации узлов конечного элемента. Следует отметить, что локальные узлы элемента могут совпадать с вершинами многоуголника
используется для локальной нумерации узлов конечного элемента. Следует отметить, что локальные узлы элемента могут совпадать с вершинами многоуголника  , а могут и не совпадать с ними, как показано на рис. 3.1. Наряду с локальной вводят сквозную глобальную нумерацию узлов. Соответствие локальных и глобальных номеров, их координаты, а также связность (т.е. указание, какие узлы образуют элемент) задаётся с помощью двух основных таблиц, которые представляют МКЭ-сетку.
, а могут и не совпадать с ними, как показано на рис. 3.1. Наряду с локальной вводят сквозную глобальную нумерацию узлов. Соответствие локальных и глобальных номеров, их координаты, а также связность (т.е. указание, какие узлы образуют элемент) задаётся с помощью двух основных таблиц, которые представляют МКЭ-сетку.

Рис. 3.1. Трехузловой, шестиузловой и десятиузловой
треугольные конечные элементы
Таблица 1. Узлы
| № | x | y | b | z |
| i | 
| 
| 
| 
|
| N |
Поле 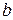 (bound) используется, чтобы отличить внутренние узлы (
(bound) используется, чтобы отличить внутренние узлы ( ) от граничных (
) от граничных ( ). Признак
). Признак  позволяет в программе, использующей эту сетку, задавать нужное граничное условие; например, если
позволяет в программе, использующей эту сетку, задавать нужное граничное условие; например, если  , ‑ то это условие Дирихле, если
, ‑ то это условие Дирихле, если  , ‑ то ставится условие Неймана, и т.д. на разных участках границы
, ‑ то ставится условие Неймана, и т.д. на разных участках границы  . Поле
. Поле  (zone) используется, чтобы задавать различные функции для коэффициентов решаемой задачи; например коэффициент теплопроводности в композитных материалах:
(zone) используется, чтобы задавать различные функции для коэффициентов решаемой задачи; например коэффициент теплопроводности в композитных материалах:  ‑ сталь,
‑ сталь,  ‑ аллюминий и т.д.
‑ аллюминий и т.д.
|
|
Таблица 1 не позволяет нарисовать МКЭ-сетку, а только узлы. Это значит, что требуется еще одна таблица элементов, или таблица связности, в которой указывались бы связи узлов ребрами и то, какие узлы образуют элемент.
Таблица 2. Элементы
| № | n1 | n2 | n3 | … | nm | z |
| j | ||||||
| M |
Строка 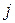 таблицы элементов показывает, что конечный элемент
таблицы элементов показывает, что конечный элемент  ‑ это треугольник с вершинами в узлах 213, 45 и 41246 и расположенный в зоне 3. Таким образом, эта таблица указывает соответствие локальных и глобальных номеров узлов. При этом локальный порядок нумерации определен заранее, например как показано на рис. 3.1. Принято, чтобы «основные» узлы элемента, т.е. узлы, совпадающие с вершинами многоугольника, нумеровались против хода часовой стрелки.
‑ это треугольник с вершинами в узлах 213, 45 и 41246 и расположенный в зоне 3. Таким образом, эта таблица указывает соответствие локальных и глобальных номеров узлов. При этом локальный порядок нумерации определен заранее, например как показано на рис. 3.1. Принято, чтобы «основные» узлы элемента, т.е. узлы, совпадающие с вершинами многоугольника, нумеровались против хода часовой стрелки.
С томощью двух таблиц – узлов и элементов – легко нарисовать МКЭ-сетку. Для этого в цикле  рисуем каждый элемент. Конечный элемент
рисуем каждый элемент. Конечный элемент  рисуется так: в строке
рисуется так: в строке 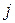 таблицы 2 последовательно берутся глобальные номера
таблицы 2 последовательно берутся глобальные номера  , для каждого из них в строках
, для каждого из них в строках  таблицы 1 берутся координаты и узлы соединяются ребрами в порядке
таблицы 1 берутся координаты и узлы соединяются ребрами в порядке  . Таким образом, таблицы узлов и элементов однозначно определяют МКЭ-сетку. На практике наряду с этими таблицами удобно пользоваться таблицами инцидентности (или таблицами соседей). Так, для фрагмента сетки, показанной на рис. 3.2 таблицы 3, 4 инцидентых узлов и элементов выглядят так (заполнены только 1-я и 19-я строки)
. Таким образом, таблицы узлов и элементов однозначно определяют МКЭ-сетку. На практике наряду с этими таблицами удобно пользоваться таблицами инцидентности (или таблицами соседей). Так, для фрагмента сетки, показанной на рис. 3.2 таблицы 3, 4 инцидентых узлов и элементов выглядят так (заполнены только 1-я и 19-я строки)
|
|

Рис. 3.2. Фрагмент МКЭ-сетки
Таблица 3. Инцидентные узлы
| № | e1 | e2 | e3 | e4 | e5 | e6 | … | ep |
| N |
Таблица 4. Инцидентные элементы
| № | k1 | k2 | k3 | k4 | k5 | k6 | … | kz |
| N |
Элементные вектора и матрицы. Элементные вклады в систему МКЭ
Преобразуем интегральное тождество (2.19) на МКЭ-сетке
 (3.2)
(3.2)
заменяя интегралы суммой интегралов по элементов и используя разложения функций по базису (3.1) внутри каждого элемента
 (3.3)
(3.3)
Здесь 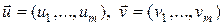 ‑ элементные вектора. Начнем с первого интеграла в (3.2).
‑ элементные вектора. Начнем с первого интеграла в (3.2).
 (3.4)
(3.4)
Здесь квадратная матрица  размерности
размерности  (число узлов элемента
(число узлов элемента  ) называется элементной матрицей масс. Отметим некоторые её свойства. Во-первых, по построению она симметрична. Во-вторых, в обшем случае она будет заполненной (примеры будут рассмотрены ниже), но если воспользоваться квадратурной формулой численного интегрирования по узлам вида
) называется элементной матрицей масс. Отметим некоторые её свойства. Во-первых, по построению она симметрична. Во-вторых, в обшем случае она будет заполненной (примеры будут рассмотрены ниже), но если воспользоваться квадратурной формулой численного интегрирования по узлам вида
 ,
,
где 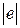 ‑ полощадь (объем) элемента
‑ полощадь (объем) элемента  , то в силу свойства базисных функций
, то в силу свойства базисных функций  получаем диагональную матрицу масс
получаем диагональную матрицу масс  .
.
Перейдем к преобразованию интеграла
 (3.5)
(3.5)
Здесь квадратная симметричная матрица  размерности
размерности  называется элементной матрицей жесткости.
называется элементной матрицей жесткости.
Интеграл по границе вычисляется следующим образом.
 (3.6)
(3.6)
Принципиальное отличие коэффициентов  от элементов матрицы масс (3.4) в том, что интегрирование в (3.6) ведется не по площади элемента
от элементов матрицы масс (3.4) в том, что интегрирование в (3.6) ведется не по площади элемента  , а лишь по той части его границы, которая лежит на границе области
, а лишь по той части его границы, которая лежит на границе области  . При этом из-за свойства
. При этом из-за свойства  среди всех коэффициентов
среди всех коэффициентов  будут отличны от нуля лишь те, для которых одновременно
будут отличны от нуля лишь те, для которых одновременно 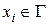 и
и  . Например, для линейного треугольного элемента, показанного на рис. 3.3, элементная матрица
. Например, для линейного треугольного элемента, показанного на рис. 3.3, элементная матрица  будет иметь следующую структуру
будет иметь следующую структуру
|
|
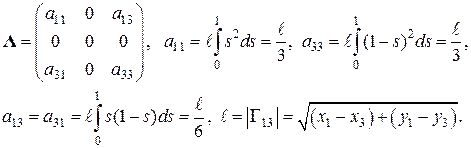 (3.7)
(3.7)

Рис. 3.2. К подсчету интеграла по границе
Перейдем к преобразованиям интегралов в правой части интегрального тождества (3.2). В первом из них обозначим  , тогда, точно так же, как (3.3) получаем
, тогда, точно так же, как (3.3) получаем
 , (3.8)
, (3.8)
где  ‑ матрица масс, определенная в (3.4), а вектор
‑ матрица масс, определенная в (3.4), а вектор  называется вектором сил или нагрузок.
называется вектором сил или нагрузок.
Наконец, интеграл по границе вычисляется так:
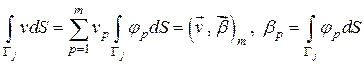 (3.9)
(3.9)
Для примера на рис. 3.2 вектор  равен
равен  .
.
Итак, интегральное тождество (3.2) можно переписать в виде суммы элементных вкладов:
 (3.10)
(3.10)