Дальневосточный государственный университет
Кафедра физической химии и физико-химических проблем экологии
Е.В. Щитовская, И.В. Григорьева
Физическая химия
В вопросах и ответах
(Применение термодинамики к фазовым равновесиям)
Методическое пособие
Владивосток
Издательство Дальневосточного университета
ББК 24.5
Щ 83
Щитовская Е.В., Григорьева И.В.
Щ 83 Физическая химия в вопросах и ответах. Применение термодинамики к фазовым равновесиям. Метод. Пособие. – Владивосток: Изд-во Дальневост. ун-та, 2006. – 25 с.
Методическое предназначено для самостоятельной подготовки студентов к сдаче коллоквиумов, экзамена по курсу «Физическая химия» составлены согласно существующей программе по физической химии для химических специальностей университетов и охватывают раздел «Термодинамика. Фазовые равновесия» курса физической химии.
Печатается по решению методической комиссии ИХПЭ ДВГУ
 ББК 24.5
ББК 24.5
ã Щитовская Е.В., Григорьева И.В.
ã Издательство Дальневосточного
университета, 2006
Применение термодинамики к фазовым равновесиям
Вопросы
1. Запишите условия равновесия (термического, механического и химического) в системе лед – жидкая вода:
2. Чему равно число степеней свободы (С) в однокомпонентной системе, если число фаз, находящихся в равновесии, равно: а) 1, б) 2, в) 3?
3. Может ли чистое вещество иметь 4 разных фазовых состава? Если да, то могут ли все 4 фазы данного вещества находиться в равновесии при каких-либо условиях?
4. Основной закон фазового равновесия – это
а) уравнение Менделеева-Клапейрона;
б) правило фаз Гиббса;
в) уравнение Клапейрона-Клаузиуса.
Выберите правильный ответ и запишите соответствующее уравнение.
5. Какова связь между основными термодинамическими параметрами однокомпонентной двухфазной системы, находящейся в состоянии равновесия?
6. Запишите условие равновесия в тройной точке.
7. Что собой представляют диаграммы состояния, и в частности диаграммы состояния однокомпонентных систем?
8. Как на диаграмме состояния однокомпонентной системы изобразится инвариантное, моно- и бивариантное состояния?
9. Эндо– или экзотермическими являются процессы плавления кристаллических веществ, испарения жидкости и сублимации твердых тел? Ответ обоснуйте.
10. В каком соотношении находятся теплота сублимации кристаллических тел и теплота испарения жидкости? Выберите правильный вариант ответа и обоснуйте его: а) DНсубл. = DНиспар .;
б) DНсубл. > DНиспар .;
в) DНсубл. < DНиспар .;
11. Что называется составляющим веществом и компонентом? Для каждой из следующих систем установите число компонентов:
а) NH4Cl(кр), NH3(г), HCl(г), где парциальное давление аммиака Р (NH3) не обязательно равно парциальному давлению хлороводорода Р (HCl);
б) СаСО3(кр), СаO(кр), СО2(г);
в) NH4Cl(кр), NH3(г), HCl(г), где Р (NH3) всегда равно Р (HCl).
12. Объясните, почему система NaCl – KCl – H2O (1) должна рассматриваться как 3-х компонентная, тогда как система КСl – NaBr – H2O (2) должна считаться 4-х компонентной?
13. Что представляют собой кривые испарения, возгонки и плавления однокомпонентной системы? Изобразить схематически диаграмму состояния воды при низких давлениях и обозначить на ней эти кривые: ОС – испарения, ОВ – плавления, ОА – возгонки.
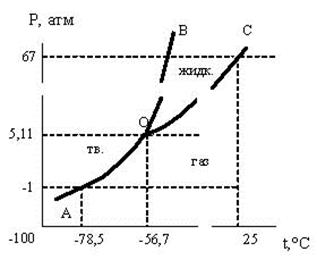
14. Каковы верхняя и нижняя границы кривых испарения жидкости, возгонки твердого вещества и плавления однокомпонентной системы?
15. Как меняется температура плавления льда и температура кипения воды с уменьшением давления? Выберите правильный вариант ответа и обоснуйте его.
а) DТпл. > DТ кип .; б) DТпл. = DТкип.; в) DТпл. < DТкип .
16. Используя уравнения Клаузиуса-Клапейрона, покажите, что вблизи тройной точки однокомпонентной системы кривая температурной зависимости давления насыщенного пара над твердым веществом имеет больший наклон, чем аналогичная кривая для жидкости.
17. Дайте определение фазовым равновесиям и приведите их примеры.
18. Дайте определение фазовым переходам I и II рода и приведите их примеры.
19. Изобразите зависимость термодинамических параметров G, S, V, H и Ср от температуры при фазовых переходах I и II рода.
20. Изобразите зависимости химического потенциала и мольного объема воды от температуры вблизи температуры плавления при Р = 1 атм.
21. Изобразите зависимости химического потенциала и мольного объема воды от температуры вблизи нормальной температуры кипения.
22. Получите уравнение для зависимости температуры плавления чистого вещества А в зависимости от давления. Какие свойства вещества будут определять, увеличится или уменьшится температура плавления при увеличении давления.
23. Можно ли использовать уравнение Клаузиуса-Клапейрона в форме  для расчета энтальпии перехода между двумя кристаллическими модификациями вещества?
для расчета энтальпии перехода между двумя кристаллическими модификациями вещества?
24. Изобразите зависимость молярной энергии Гиббса вещества от температуры и объясните ее.
25. Зависит ли температура фазовых переходов от давления? Если да, то, каким (или какими) уравнениями описывается эта зависимость?
26. Возможно ли существование метастабильных состояний при фазовых переходах? Если да, то приведите примеры.
27. Что такое стабильное, метастабильное и нестабильное равновесие? Приведите примеры.
28. Как рассчитать, при каком давлении температура плавления льда понизится от 0 до 1º С? Нужны ли для этого дополнительные справочные данные.
29. Зависит ли давление пара над чистой жидкостью, энтальпия и энтропия испарения от числа молей вещества?
30. Как из справочных данных определить, при каком давлении пары йода будут находиться в равновесии с кристаллическим йодом при 25 0 С? Что будет, если при этой температуре увеличить (уменьшить) давление?
31. Как их справочных данных рассчитать давление насыщенного пара сульфурилхлорида SO2Cl2 при 25º С? Что произойдет, если при этом давлении увеличить (уменьшить) температуру?
32. Как их справочных данных определить, что устойчивее при 25º С и 1 атм – ромбическая или моноклинная сера? При какой температуре при стандартном давлении ромбическая и моноклинная сера будут находиться в равновесии?
33. Зависимость давления насыщенного пара перфторорганического соединения, использующегося в качестве компонента искусственной крови, от температуры имеет вид  (T,K; P,Па), где a, b, c – постоянные. Найдите зависимость энтальпии и энтропии испарения этого соединения от температуры.
(T,K; P,Па), где a, b, c – постоянные. Найдите зависимость энтальпии и энтропии испарения этого соединения от температуры.
34. Стандартная энтальпия образования твердого 1-фминоадамантана (C10H15NH2), который является основой противовирусного препарата «Мидантан», равна DН0 при 298 К. Зависимость давления насыщенного пара над твердым соединением может быть выражена уравнением:  (T, K). Как рассчитать DfН0 DfU0 при 298 К для газообразного 1-аминоадамантана?
(T, K). Как рассчитать DfН0 DfU0 при 298 К для газообразного 1-аминоадамантана?
35. Почему «сухой лед» (твердый углекислый газ) при обычных условиях испаряется, а «обычный» лед плавится?
36. Изобразите диаграмму состояния углекислого газа. Покажите, как меняется число фаз, находящихся в равновесии, и число степеней свободы при изменении температуры одного моля СО2 от 100º С до 25º С при Р = 1 атм. Изменится ли ответ, если рассматривать систему из двух молей СО2?
Ответы
1. Ответ
а) Тлед = Твода ж; б) Рлед = Рвода ж; в) mлед = mвода ж;
2. Ответ
Для однокомпонентной системы С = К + 2 – Ф, К = 1, f = 3 – Ф.
а) С = 2, б) С = 1, в) С = 0.
3. Ответ
Не существует каких-либо ограничений для общего числа фаз любой системы. Например, для воды известны 7 типов льдов, жидкая вода и пар. Для углерода известны 2 твердые фазы, но жидкий углерод до сих пор еще не получен – этому отвечают пока экспериментально недостижимые значения Т и Р. Однако при равновесии число одновременно существующих фаз не является произвольным. Оно определяется правилом фаз Гиббса. Для чистого вещества С = 3 – Ф, если Ф = 4, то С = –1 – не имеет смысла. Например, С = 0 при Ф = 3, т.е. максимальное число фаз, находящихся в равновесии равно 3. Если число фаз больше трех, то имеется несколько тройных точек.
4. Ответ
б) С = К + 2 – Ф, 2 – два внешних термодинамических параметра (Р и Т).
5. Ответ
Это зависимость Р = f (Т), даваемая уравнением Клапейрона-Клаузиуса 
6. Ответ
Pi0ж.ф. = Pi0тв.ф., где P0 – давление насыщенного пара вещества i над соответствующей фазой, жидкой и твердой; mI(тв) = mI(ж) = mI(п), где mI – химический потенциал.
7. Ответ
Диаграммы состояния – это графики в различных координатах, выражающие фазовые состояния и условия равновесного сосуществования фаз в гетерогенной системе.
Состояние однокомпонентной системы вполне определяется двумя независимыми параметрами. Поскольку в соответствии с правилом фаз Гиббса для такой системы С = 3 – Ф, и максимальное число степеней свободы при наличии только одной фазы равно двум, т.е. изменять независимо друг от друга без изменения числа фаз, находящихся в равновесии, можно 2 параметра, например, давление Р и температуру Т, а объем системы V = f(P,T).
Если по трем координатным осям отложить, соответственно, давление, температуру и объем системы, то полученная пространственная диаграмма, выражающая зависимость состояния системы и фазовых равновесий в ней от внешних условий, называется диаграммой состояния или фазовой диаграммой. Построение таких пространственных диаграмм связано с определенными трудностями, и они мало удобны для практического применения. Для характеристики состояния однокомпонентных систем чаще используют плоскую фазовую диаграмму, представляющую собой проекцию пространственной диаграммы состояния на плоскость Р–Т.
В двух- и многокомпонентных системах состояние каждой фазы определяется однозначно, если заданы Р, Т и состав этой фазы. Поэтому, например, двухкомпонентные системы обычно представляют графически в координатах Р – состав (Т = const) или Т – состав (Р = const).
8. Ответ
На Р,Т диаграммах однокомпонентных систем инвариантные системы (С = 0) изобразится в виде точек (тройных, т.к. Ф = 3), моновариантные в виде линий (С = 1 при Ф = 2) и бивариантные (С = 2 при Ф = 1) в виде участков плоскости (областей или полей).
9. Ответ
Для процессов сублимации твердых тел, испарения жидкостей переход в газовую фазу связан с преодолением энергии межмолекулярного взаимодействия, поэтому всегда сопровождается поглощением теплоты:
DНсубл . > 0 и DНиспар . > 0. С термодинамической точки зрения для этих процессов DНф.п . = Тф.п.·(Sг – Sж.), Sг > Sтв., Sг > Sж., т.е. DНсубл. > 0 и DНиспар. > 0.
Для плавления переход к жидкой фазе также связан с поглощением некоторого количества теплоты DНпл. = Тпл.(Sж – Sтв.), Sж > Sтв ., поэтому DНпл. > 0, и, следовательно, все эти процессы являются эндотермическими.
10. Ответ
б) DНсубл. > DНиспар .; так как в соответствии с законом Гесса: тв ® газ
DНсубл .
DНпл . ë ж û DНисп .
DНсубл. = DНпл. + DНисп ., поскольку DНпл. > 0, то DНсубл.> DНисп . (вблизи тройной точки).
11. Ответ
Составляющими веществами называются все индивидуальные химические вещества, которые могут быть выделены из равновесной системы (простыми препаративными методами – кристаллизацией, испарением, конденсацией и др.) и существовать вне её.
Компонентами называют независимые составляющие вещества, т.е. вещества, наименьшее число которых необходимо и достаточно для образования всех возможных фаз данной системы. При этом число компонентов (К) равно числу составляющих веществ (N) минус число уравнений (Е), связывающих концентрации составляющих веществ в равновесной системе:
К = N – Е.
а) N = 3 (NH4Cl, NH3, HCl,); E = 1; (NH4Cl = HCl(г) + NH3); K = 3 – 1 = 2
б) N = 3 (СаО, СаСО3, СО2); Е = 1 (СаСО3 = СаО + СО2); К = 3 – 1 = 2
в) N = 3 (NH4Cl, HCl, NH3); E = 2 (NH4Cl = HCl(г) + NH3); Р NH3 = P HCl;
K = 3 – 2 = 1
12. Ответ
Если К – число компонентов, N – число составляющих веществ и Е – число уравнений, связывающих их концентрации в равновесной гетерогенной системе, то К = N – Е.
· Для системы (1) N = 3 (NaCl, KCl, H2O), Е = 0, К = 3, т.е. система 3-х компонентная,
· для второй системы (2) N = 5 (КСl, NaBr, КBr, NaСl, Н2О), Е = 1, т.к. КСl + NaBr = КBr + NaСl, поэтому К = 5 – 1 = 4
13. Ответ
Кривые Р = f(Т), представляющие условия равновесия между жидкостью и паром, твердой фазой и паром, твердой фазой и жидкостью, называются соответственно кривыми испарения, возгонки (сублимации) и плавления.
14. Ответ
Верхняя граница кривой испарения – критическая температура, нижняя граница кривой испарения определяется областью метастабильного состояния переохлажденной жидкости. Верхней границей кривой сублимации всех веществ является точка плавления (тройная точка). Перегреть кристаллическое вещество выше его температуры плавления не удается, т.к. происходит разрушение кристаллической решетки. Нижняя граница находится (теоретически) при абсолютном нуле, если не образуется новой фазы, т.е. другой кристаллической модификации.
Кривая плавления продолжается вверх с соответствующим наклоном, пока не будут достигнуты такие давление и температура, при которых оказывается более устойчивой другая кристаллическая модификация. После перехода твердого вещества в другую модификацию на кривой плавления появляется другой наклон, зависящий от новых значений Тф.п., DНпл., Vтв. и Vж этой кристаллической модификации. Внизу кривая плавления заканчивается в тройной точке, т.к. при меньшем давлении и кристаллы и жидкость переходят в пар.
15. Ответ
Зависимость температуры плавления (Тпл .) льда от давления – это кривая ОВ. Как видно из диаграммы состояния воды, при понижении давления Тпл . льда увеличивается. Кривая испарения жидкой воды ОС, и при понижении давления Ткип . воды уменьшается. Чтобы получить соотношение между DТпл . и DТкип ., воспользуемся уравнением Клаузиуса-Клапейрона: 
Для процесса плавления  , т. к. Vж< Vтв., DНпл > 0, то
, т. к. Vж< Vтв., DНпл > 0, то 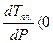 и, следовательно, при понижении давления Тпл . льда увеличивается.
и, следовательно, при понижении давления Тпл . льда увеличивается.
При Тпл .= 273 К, Vж = 1,000 см3/г и Vтв . = 1,0908 см3/г, D Нпл . = 79,7 кал/г = 79,7 кал/г × 41,29 см3атм./кал = 3290,8 см3атм./г

Для процесса испарения жидкой воды  , Ткип . = 373 К, D Нисп .= 539,7 кал/г = 539,7×41,29 см3атм/г = 22284,2 см3атм/г. Vп = 1651 см3/г, Vж = 1 см3/г.
, Ткип . = 373 К, D Нисп .= 539,7 кал/г = 539,7×41,29 см3атм/г = 22284,2 см3атм/г. Vп = 1651 см3/г, Vж = 1 см3/г.
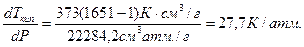 Таким образом, D Ткип . > D Тпл ., в отличие от процесса плавления температура кипения очень сильно зависит от давления, увеличиваясь с его повышением. Это связано с большой величиной изменения объема (D V), при переходе жидкости в пар. Отношение
Таким образом, D Ткип . > D Тпл ., в отличие от процесса плавления температура кипения очень сильно зависит от давления, увеличиваясь с его повышением. Это связано с большой величиной изменения объема (D V), при переходе жидкости в пар. Отношение  и
и 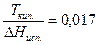 , в то время как D Vисп . = 1650 см3/г, а D Vпл .= – 0,0907 см3/г.
, в то время как D Vисп . = 1650 см3/г, а D Vпл .= – 0,0907 см3/г.
16. Ответ
В соответствии с уравнением Клаузиуса-Клапейрона, зависимость давления насыщенного пара от температуры для равновесия двух фаз 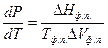 , наклон кривых возгонки (тв Û г) и испарения (ж Û п) зависит от теплоты фазового перехода, температуры и изменения объема:
, наклон кривых возгонки (тв Û г) и испарения (ж Û п) зависит от теплоты фазового перехода, температуры и изменения объема:
DVпл = Vп – V тв. и Dисп. = Vп – Vж. Поскольку Vп >> Vтв. и Vп >> Vж, то вблизи тройной точки наклон Р(Т) кривой определяется величиной D Нф . п. В соответствии с законом Гесса DНвозг. = DНпл.+ DНисп ., поэтому DНсубл. > DНисп . и 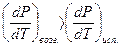 , так что вблизи тройной точки кривая возгонки имеет бóльший наклон, чем кривая испарения.
, так что вблизи тройной точки кривая возгонки имеет бóльший наклон, чем кривая испарения.
17. Ответ
Равновесие в гетерогенных системах, т.е., состоящих из нескольких фаз,в которых не происходит химического взаимодействия между компонентами, а протекают лишь процессы перехода компонентов из одной фазы в другую (или в другие), называется гетерогенным или фазовым. К ним относятся равновесия типа: Т1 Û Т2; Т Û Ж; Т Û Г; Ж1 Û Ж2; Ж Û Г.
18. Ответ
Фазовыми переходами, или фазовыми превращениями, называют равновесные при постоянных температуре и давлении переходы вещества из одной фазы в другую. Фазовые переходы I рода сопровождаются тепловыми эффектами и изменением удельного объема. Согласно Эренфесту, при фазовых переходах I рода (испарение, плавление, возгонка) скачкообразно меняется как первые производные от энергии Гиббса по температуре и давлению, т.е. энтропия и объем, так и вторые производные энергии Гиббса: теплоемкость – Ср, коэффициент термического расширения – 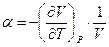 ; сжимаемость –
; сжимаемость – 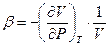 .
.
Фазовые переходы II рода – переходы вещества из одной фазы в другую без теплового эффекта и изменения удельного объема, но скачкообразно меняются Ср, b, a, т.е. вторые производные энергии Гиббса:  ;
;  ;
;  .
.
К фазовым переходам II рода относятся переходы жидкого гелия в сверхтекучее состояние Не-I Û Не-II, железа из ферромагнитного в парамагнитное состояние, металла из обычного в сверхпроводящее состояние, переход «порядок - беспорядок» в сплавах типа b-латуни и др.
19. Ответ
Изменение термодинамических параметров при фазовых переходах I-го и II-го родов представлены на рис. 1, где Тtr – температура равновесного фазового перехода вещества из фазы i в фазу j. Как видно, при фазовых переходах II рода первые производные не претерпевают скачков.

Рис. 1. Изменение термодинамических функций при фазовых переходах I-го и II-го рода.
20. Ответ
Из диаграммы состояния воды видно, что изобара при Р = 1 атм пересекает кривую плавления в точке, отвечающей температуре плавления льда, при которой существуют фазовое равновесие Н2О(лед) Û Н2О(ж) и D m = 0, т.е. m(лед) = m(ж). Для индивидуального вещества химический потенциал представляет собой молярное значение энергии Гиббса  , а
, а 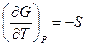 , и зависимость химического потенциала от температуры для твердой и жидкой фаз выражается соответствующими уравнениями:
, и зависимость химического потенциала от температуры для твердой и жидкой фаз выражается соответствующими уравнениями:
 и
и  . Поскольку величина энтропии всегда положительна, то химические потенциалы жидкой воды и льда вблизи температуры плавления убывают линейно, а наклоны прямых определяются величиной энтропии: Sлед< Sж, поэтому
. Поскольку величина энтропии всегда положительна, то химические потенциалы жидкой воды и льда вблизи температуры плавления убывают линейно, а наклоны прямых определяются величиной энтропии: Sлед< Sж, поэтому 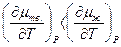 , т.е. mж = f(T) идет круче.
, т.е. mж = f(T) идет круче.
Объем твердой и жидкой фаз с повышением температуры увеличивается, а при Т = Тпл . объем меняется скачком, причем Vльда > Vж для воды (DV ¹ 0).
21. Ответ
При температуре кипения между жидкой водой и паром устанавливается гетерогенное равновесие, относящееся к фазовым переходам I рода:
Н2О(ж) Û Н2О(пар), условием которого является равенство химических потенциалов: m(ж)= m(пар) или Dmисп. = 0. При повышении температуры m(ж) и m(пар) уменьшается, т.к.  , а S всегда положительна. Чем больше S, тем круче идет кривая m = f(T). Поскольку S(пар) > S(ж), то убывание функции m(ж) = f(T) отразится на графике более пологой кривой, чем m(пар) = f(T).
, а S всегда положительна. Чем больше S, тем круче идет кривая m = f(T). Поскольку S(пар) > S(ж), то убывание функции m(ж) = f(T) отразится на графике более пологой кривой, чем m(пар) = f(T).
Энтропия жидкой воды меньше, чем энтропия пара S(ж) < S(пар) и при Ткип . энтропия меняется скачком: S(пар) – S(ж) = DS(исп.).
22. Ответ
Уравнение зависимости Тпл. = f(P) можно получить из уравнения Клаузиуса-Клапейрона для равновесия Т = Ж
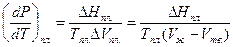 ,
,  . Поскольку D Нпл .> 0, то характер изменения Тпл. с давлением зависит от знака DV: если Vж > Vтв. для вещества А, то
. Поскольку D Нпл .> 0, то характер изменения Тпл. с давлением зависит от знака DV: если Vж > Vтв. для вещества А, то  и с повышением давления Тпл . увеличится. Если же Vж < Vтв . для вещества В (как у воды), то DV< 0,
и с повышением давления Тпл . увеличится. Если же Vж < Vтв . для вещества В (как у воды), то DV< 0, 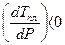 и с повышением давления Тпл . понизится.
и с повышением давления Тпл . понизится.
23. Ответ
Нет, эта форма уравнения является частным случаем уравнения Клаузиуса-Клапейрона:  . Оно может быть применено к процессам возгонки твердого вещества и испарения жидкости, когда DV » Vп (Vп >> Vтв. и Vп >> Vж) и пар ведет себя как идеальный газ Vп =
. Оно может быть применено к процессам возгонки твердого вещества и испарения жидкости, когда DV » Vп (Vп >> Vтв. и Vп >> Vж) и пар ведет себя как идеальный газ Vп = 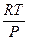 , тогда
, тогда  или
или  .
.
24. Ответ
При изменении температуры индивидуального вещества меняется его агрегатное состояние, т.е. происходят фазовые переходы. В изобарно-изотермическом процессе перехода вещества из состояния 1 в состояние 2 D G = G2 – G1 £ 0, и, следовательно, процесс возможен, если G2 < G1, при этом вещество переходит из фазы 1 с бόльшим значением энергии Гиббса G1 в фазу 2 с меньшим значением G2. При Т = Тф.п. DG = 0, т.е. переход вещества из одной фазы в другую не сопровождается изменением энергии Гиббса и может происходить в обоих направлениях, при этом две фаза (два агрегатных состояния) находятся в равновесии. Для каждого агрегатного состояния G является функцией температуры: Gтв.(Т), Gж(Т), Gг(Т), но по-разному изменяются с температурой, поскольку производная энергии Гиббса по температуре  = –S, а энтропия разных агрегатных состояний существенно различаются: Sтв < Sж < Sг. В соответствии с этим убывание функции Gтв.(Т) на графике отразится более пологой кривой, чем функция Gж(Т), а последней, в свою очередь, - более пологой кривой, чем Gг(Т). При определенных значениях температуры эти зависимости G(Т) пересекаются: при температуре отвечающей точке пересечения кривых Gтв.(Т) и Gж(Т), DG = 0, в равновесии находятся твердая и жидкая фазы, и таким образом, эта точка является точкой плавления (Тпл .). В точке пересечения кривых Gж(Т) и Gг(Т) при определенном давлении будут сосуществовать жидкая и газообразная фазы, и это будет точка кипения (Ткип .) при заданном давлении. При Т' < Тпл . устойчивой является твердая фаза, т.к. Gтв.< Gж, а при Т'' < Тпл – жидкая фаза, т.к. Gж. < Gтв ..
= –S, а энтропия разных агрегатных состояний существенно различаются: Sтв < Sж < Sг. В соответствии с этим убывание функции Gтв.(Т) на графике отразится более пологой кривой, чем функция Gж(Т), а последней, в свою очередь, - более пологой кривой, чем Gг(Т). При определенных значениях температуры эти зависимости G(Т) пересекаются: при температуре отвечающей точке пересечения кривых Gтв.(Т) и Gж(Т), DG = 0, в равновесии находятся твердая и жидкая фазы, и таким образом, эта точка является точкой плавления (Тпл .). В точке пересечения кривых Gж(Т) и Gг(Т) при определенном давлении будут сосуществовать жидкая и газообразная фазы, и это будет точка кипения (Ткип .) при заданном давлении. При Т' < Тпл . устойчивой является твердая фаза, т.к. Gтв.< Gж, а при Т'' < Тпл – жидкая фаза, т.к. Gж. < Gтв ..
25. Ответ
Температура фазовых переходов, как первого, так и второго рода является функцией давления. Для фазовых переходов I рода (плавление, возгонка, испарение) эта зависимость описывается дифференциальным уравнением Клаузиуса – Клапейрона для равновесного существования фаз:  . Для фазовых переходов II рода, где нет существования фаз, Р от Тф.п.II выражается одним из уравнений Эренфеста:
. Для фазовых переходов II рода, где нет существования фаз, Р от Тф.п.II выражается одним из уравнений Эренфеста:  и
и 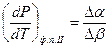 , где
, где  - коэффициент термического расширения,
- коэффициент термического расширения,  – изотермический коэффициент сжимаемости. Как видно, зависимости Р = f (Tф.п.) задаются с помощью тех термодинамических свойств, которые изменяются при переходе от одной фазы к другой. В случае фазовых переходов I рода это DНф.п. ≠ 0 и DVф.п. ≠0, а для фазовых переходов II рода это DСр ≠ 0, Da ≠ 0, Db ≠ 0. Интересно, что последние величины – первые производные от тех, которые скачкообразно изменяются при фазовых переходах I рода.
– изотермический коэффициент сжимаемости. Как видно, зависимости Р = f (Tф.п.) задаются с помощью тех термодинамических свойств, которые изменяются при переходе от одной фазы к другой. В случае фазовых переходов I рода это DНф.п. ≠ 0 и DVф.п. ≠0, а для фазовых переходов II рода это DСр ≠ 0, Da ≠ 0, Db ≠ 0. Интересно, что последние величины – первые производные от тех, которые скачкообразно изменяются при фазовых переходах I рода.
26. Ответ
При фазовых переходах I рода имеется возможность существования метастабильных состояний, например, переохлажденной или перегретой жидкости, пересыщенного пара, которые наблюдаются иногда при медленном переходе через температуру фазового перехода Тф.п.I (Ttr). Условия метастабильного равновесия выражаются с помощью обычных соотношений термодинамики, например DG = 0 и  .
.
При фазовых превращениях II рода не существует метастабильных состояний, и каждая фаза может существовать только в определенной температурной области. Эти переходы осуществляются без появления и исчезновения фазовых границ, без явления «переохлаждения».
27. Ответ
При стабильном равновесии энергия Гиббса достигает минимума, и всякое отклонение от этого состояния приводит к возрастанию энергии Гиббса (G) системы. Поэтому система самопроизвольно возвращается к равновесному состоянию.
При метастабильном равновесии система так же, как и при стабильном равновесии достигает минимума энергии Гиббса, но этот минимум не является абсолютным. Система может находиться в другом состоянии, которому отвечает еще меньшее значение G, и может перейти самопроизвольно в это состояние, которое представляет собою уже стабильное равновесие. Например, возможно метастабильное равновесие между серой жидкой переохлажденной, серой твердой ромбической перегретой и серой в виде пересыщенного пара. Энергии Гиббса всех трех фаз одинаковы: Gж Gтв. Gг, но существует еще моноклиническая твердая сера. Если в систему ввести даже незначительную крупицу моноклинической серы, метастабильное равновесие нарушится, и система переходит к стабильному равновесию, которому отвечает сера моноклиническая и равновесный с ней насыщенный пар.
При нестабильном состоянии (неустойчивом равновесии) всякое изменение системы связано с уменьшением энергии Гиббса, и раз начавшись, это изменение переводит всю систему в новое более устойчивое состояние. Например, пересыщенный пар воды в очень чистых условиях может сохраняться некоторое время без изменения, но появление даже ничтожной капли жидкой воды вызывает конденсацию, при которой часть пара переходит в жидкую воду, и получается устойчивая система из воды и насыщенного пара.
28. Ответ
Зависимость температуры плавления от давления определяется уравнением Клаузиуса-Клапейрона:  ,
, 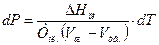 . Проинтегрируем его при условии, что DНпл. = const и (Vж–Vтв.) = const.
. Проинтегрируем его при условии, что DНпл. = const и (Vж–Vтв.) = const.
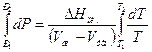 ,
, 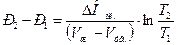 ; если Т1 =273К при Р1 =1атм-1,0133×105 Па, а Т2 = 272 при Р2, то
; если Т1 =273К при Р1 =1атм-1,0133×105 Па, а Т2 = 272 при Р2, то 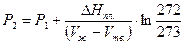 ; D Нпл .= 6025 Дж/моль, Vж = 18 мл/моль, Vтв . = 19,8 мл/моль.
; D Нпл .= 6025 Дж/моль, Vж = 18 мл/моль, Vтв . = 19,8 мл/моль.
Р2 = 1,0133×105 Па + 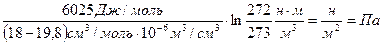 ;
;
Р2 = 1,0133×105 – 3347×106(-0,00367) = 1,0133×105 + 12,28×106 = 123,833×105 Па = 122,2 атм.
29. Ответ
Давление пара над жидкостью Р, DНисп. и Sисп . – это свойства вещества, но если Р – это интенсивное свойство, не зависящее от количества вещества, то DНисп. и Sисп . – это экстенсивные (емкостные) свойства, поэтому они зависят от числа молей вещества.
30. Ответ
I2(тв) Û I2(г) Из справочника найдем DfG°298 (I2(г)) = 19,39 кДж/моль; DfG°298 (I2(тв)) = 0, где DfG°298 – энергияГиббса образования вещества при Т = 298 К и Р = 1 атм. DfG°(испар) = 19,39 – 0 = 19,39 кДж/моль > 0, т.е. при Т = 298 К и Р = 1 атм более устойчивым является I2(тв), и пары йода не находятся в равновесии с кристаллическим йодом. Чтобы достичь равновесия при Т = 298 К, нужно изменить давление, поскольку 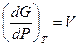 и
и 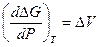 , а DV = Vг – Vтв > 0, то при увеличении давления DG увеличивается, а при уменьшении – увеличивается, а при уменьшении – DG уменьшается. Следовательно, чтобы достичь равновесия I2(тв) Û I2(г) нужно уменьшить внешнее давление. Если считать газообразный I2 идеальным газом и DV = Vг =
, а DV = Vг – Vтв > 0, то при увеличении давления DG увеличивается, а при уменьшении – увеличивается, а при уменьшении – DG уменьшается. Следовательно, чтобы достичь равновесия I2(тв) Û I2(г) нужно уменьшить внешнее давление. Если считать газообразный I2 идеальным газом и DV = Vг =  , то рассчитать давление, при котором будет достигнуто равновесие, можно по уравнению
, то рассчитать давление, при котором будет достигнуто равновесие, можно по уравнению 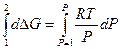
31. Ответ
Насыщенный пар – это пар, находящийся в равновесии с жидкостью или твердой фазой при Т и Р = const. Рнас.пара = Ратм ., а Т = Ткип. DG = 0 (условие равновесия). Ткип. – 298 К (по условию). SO2Cl2 (ж) Û SO2Cl2 (г).
Другой вариант решения – с помощью изотермы химической реакции:
DG = DG°298 + RT×ln P(SO2Cl2) = 0; Нужны справочные данные по DfG°298.
RT×ln P(SO2Cl2) = – DG°298; DrG°298 = DfG°298 (г) – DfG°298 (ж) = – 318,85 + 321,49 = 2,64 кДж/моль;  =0,345 атм. т.е. при Т = 298 К и Р = 1 атм. Жидкий SO2Cl2 не будет кипеть.
=0,345 атм. т.е. при Т = 298 К и Р = 1 атм. Жидкий SO2Cl2 не будет кипеть.
Чтобы выяснить влияние температуры на данное равновесие, необходимо знать тепловой эффект реакции DH°298 = DH°298(г) – DH°298(ж).
DrH°298 = -363,17 + 394,13 = 30,96 кДж/моль > 0
Кр = РSO2Cl2;  , поскольку DH ° > 0, то при увеличении температуры давление насыщенного пара будет возрастать.
, поскольку DH ° > 0, то при увеличении температуры давление насыщенного пара будет возрастать.
32. Ответ
Чем меньше DfG°298, тем устойчивее модификация. Из справочника находим DfG°298(ромб.S) = 0, DfG°298(мон.S) = 0,19 кДж/моль, DfG°298(ромб.S) < 0, DfG°298(мон.S), поэтому устойчивее ромбическая сера.
Sромб. Û Sмон . Если ромбическая и моноклинная сера находятся в равновесии, то  ; DrG°T = 0, Поскольку
; DrG°T = 0, Поскольку  , то
, то 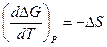
DG°T – DG°298 = – 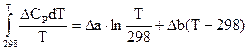 ; DCP = Da + DbT,
; DCP = Da + DbT,
или, если считать, что в интервале температур 298 – Т DS = const = DS°298
DS° = Sм – Sp = 32,55 – 31,92 = 0,63 (Дж/моль×К)
DG°298 = DS(T – 298) = DS°×T - DS °× 298.
T = 
33. Ответ
Давление насыщенного пара – это давление пара, находящегося в равновесии с жидкостью: A(ж) Û А(п). Можно записать константу Кр этого равновесия: Кр = Р(А), где Р(А) – давление насыщенного пара. В соответствии с уравнением изобары реакции 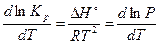 , откуда
, откуда
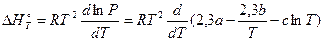
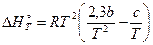 – это зависимость энтальпии испарения от температуры.
– это зависимость энтальпии испарения от температуры.
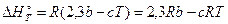 ;
; 
34. Ответ
Насыщенный пар над твердым веществом – это пар, находящийся в равновесии с твердым веществом:
С10Н15NH2 (тв.) Û С10Н15NH2 (г)
Константа этого гетерогенного равновесия Кр = Р (С10Н15NH2 (г)) = Р.
Тепловой эффект этой реакции (возгонка) можно найти из уравнения изобары Вант – Гоффа:  ;
;
 ,
,
 при Т = 298 К, DН0возг.=8,314 Дж/моль.
при Т = 298 К, DН0возг.=8,314 Дж/моль.
По закону Гесса DrH°298 = DfH°298 (С10Н15NH2 (г)) – DfH°298 (С10Н15NH2 (тв.)) = DH°возг.,
Откуда DfH°298 (С10Н15NH2 (г)) = DH°возг. – DfH°298 (С10Н15NH2 (тв.)) = 8,314(2,3В – 298С) + DfH°298 (С10Н15NH2 (тв.)).
Этот тепловой эффект [DfH°298 (С10Н15NH2 (г))] относится к реакции:
10Сграф. + 8,5Н2 + 0,5N2 ® С10Н15NH2 (г), Dnг = 1 – 9 = – 8.
DH = DU + DnгRT; DU(г) = DН(г) + 9 · 8,314 · 298
35. Ответ
Тройная точка для воды находится при Р = 4,58 мм рт. ст. (0,006 атм.) и t = 0,01 ° С, а для СО2 при Р = 5,11 атм. и t = - 56,6 ° С. Поэтому при температуре 18 – 20 ° С и давлении 1 атм. лед плавится, а твердый СО2 испаряется.

а б
Рис. 2. Фазовые диаграммы воды (а) и диоскида углерода (б).
36. Ответ
Плоская Р,Т – диаграмма состояния СО2. АО – линия возгонки СО2(тв.) СО2(г); ВО – линия плавления СО2(тв.) СО2(ж); СО – линия испарения СО2(ж) СО2(г);

Рис. 3. Фазовая диаграмма диоскида углерода.
т.к. Р = 1атм. = const, то правило фаз Гиббса имеет следующий вид: С = 2 – Ф в т. (Т = – 1000С, Р = 1атм) – система гомогенная, однофазная тв. СО2. Число степеней свободы С = 2 – Ф = 1, т.е. в определенных пределах можно изменять температуру без изменения числа фаз и вида системы. При достижении t = 78,5° С система становится гетерогенной: тв. Û г. Число степеней свободы уменьшается С = 2 – 2 = 0, т.е. при Р = 1 атм.существует единственна