Теория и практика оперируют различными методами оценки риска, многообразие которых вызвано множеством рисков и рисковых ситуаций. Анализ этих методов позволяет выделить следующие их группы.
1. Математические, статистические методы. Обычно применяются для оценки рисков частых и однородных событий, оценки количественного размера риска, к ним относятся: теория игр, теория статистических решений, теория дифференциального исчисления, имитационное моделирование и др.
2. Теоретическое описание систем (процессов) и построение причинно-следственных связей. Наиболее эффективно для оценки рисков редких или уникальных событий, нацелено на оценку качественных и количественных характеристик риска. К нему относятся: морфологический подход, метод построения деревьев и др.
3. Экспертные методы. Применяются при оценке индивидуальных, специфических рисков, открытии новых рынков, т.е. во всех отраслях экономики при отсутствии аналогов, высоком риске; оценивают количественные и качественные стороны риска.
Разнообразные методы тем не менее предполагают в своей основе расчет «классических» показателей степени (уровня) риска математического ожидания, дисперсии, стандартного отклонения, вероятности. Кратко охарактеризуем указанные показатели.
Оценка риска в условиях частичной неопределенности, связанной с разной информированностью и/или разной степенью неполноты информации у лиц, принимающих решение относительно управления каким-либо риском, традиционно происходит в рамках так называемых «игр с природой», математическая модель которыхотражает основные ситуации риска (неопределенности) описывает:
ü множество заинтересованных сторон (игроков, субъектов, \ участников);
ü возможные действия каждой из сторон, именуемые также стратегиями или ходами;
ü интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.
Пусть у нас имеются два игрока, при этом игрок 1 выступает сознательно действующий участник игры, а игрок 2 - «природа» как участник, который только отражает какую-либо объектную действительность или ее изменения. Пусть игрок 1 имеет m возможных стратегий: А1. А2...., Ат, а у природы имеется п возможных состояний (стратегий): П1, П2,..., Пn тогда условия игры с природой задаются матрицей выигрышей А игрока 1:
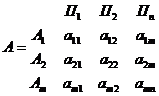 (1)
(1)
Возможен и другой способ задания матрицы игры с природой: не в виде матрицы выигрышей, а в виде так называемой матрицы рисков
R = 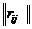 тп или матрицы упущенных возможностей.
тп или матрицы упущенных возможностей.
Величина риска - это размер платы за отсутствие информации о состоянии среды. Матрица R может быть построена непосредственно из условий задачи или на основе матрицы выигрышей.
Риском rij игрока при использовании им стратегии Ai и при состоянии среды Пj считается разность между выигрышем, который игрок получил бы, если бы он знал, что состоянием среды будет Пj, и выигрышем, который игрок получит, не имея этой информации. Зная состояние природы (стратегию) Пj игрок выбирает ту стратегию, при которой его выигрыш максимален, т.е.
rij= 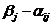 , (2)
, (2)
где
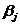 = max
= max 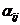 при заданном j
при заданном j
1 ≤ i ≤ m
Например, для матрицы выигрышей
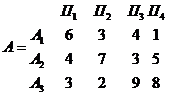 (3)
(3)
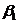 =6,
=6, 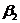 =7,
=7, 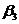 =9,
=9, 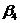 =8
=8
Согласно приведенным определениям rij и 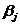 получаем матрицу рисков:
получаем матрицу рисков:
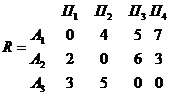 (4)
(4)
Независимо от вида матрицы выбирается такая стратегия игрока, которая была бы наиболее выгодной по сравнению с другими.
Методы оценки риска для принятия экономических решений формируются и обосновываются в рамках так называемой теории статистических решений. При этом в случае «доброкачественной или стохастической, неопределенности, когда состоянием природы поставлены в соответствие вероятности, заданные экспертно либо вычисленные, оценка риска (принятие решения) обычно принимается на основе критерия максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска (матрицы типа А либо R). Если для некоторой игры с природой, задаваемой платежной матрицей А=||aij||m стратегиям природы Пj соответствуют вероятности рj, то лучшей стратегией игрока 1 будет та, которая обеспечит ему максимальный средний выигрыш, т.е.
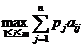 , (5)
, (5)
Применительно к матрице рисков (матрице упущенных выгод) лучшей будет та стратегия игрока, которая обеспечивает ему минимальный средний риск:
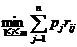 (6)
(6)
Математически установлено, что критерии (3), (4) эквивалентны в том смысле, что оптимальные значения для них обеспечивает одна и та же стратегия Ai игрока 1.
Например, для игры, задаваемой матрицей выигрышей или матрицей рисков, при условии, что p1=p2=p3=p4= 1/4, А3 - лучшая стратегия игрока 1 по критерию (4), поскольку
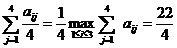 (7)
(7)
Эта же стратегия лучшая для игрока 1 относительно обеспечения минимального уровня риска:
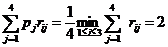 (8)
(8)
На практике целесообразно отдавать предпочтение матрице выигрышей или матрице рисков в зависимости от того, какая из них определяется с большей достоверностью, что особенно важно учитывать при экспертных оценках элементов матриц.
Максимум ожидаемого среднего значения может быть pacсчитан с использованием абсолютных значений стратегии ситуации и вероятности (частоты, удельного веса) каждой стратег (ситуации):
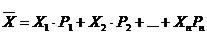 , (9)
, (9)
где 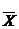 - среднее ожидаемое значение мероприятия (ситуации)
- среднее ожидаемое значение мероприятия (ситуации)
X — абсолютное значение мероприятия (ситуации);
Р — вероятность (частота, удельный вес) мероприятия (ситуации);
n — количество (число) случаев наблюдения, мероприятий (ситуаций).
В целом среднее значение не позволяет принять окончательное и объективное решение в пользу какой-либо стратегии (ситуации), так как представляет собой обобщенную количественную; характеристику. Дополнительно к этому критерию рассчитываются показатели среднего квадратического отклонения, дисперсии и вариации.
Среднее квадратическое отклонение характеризует колеблемость (изменчивость) возможного результата стратегии (ситуации) от средней величины. Дисперсия представляет собой среднее взвешенное из квадратов отклонений действительных результатов от средних ожидаемых:
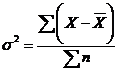 , (10)
, (10)
где 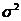 -дисперсия.
-дисперсия.
Среднее квадратическое отклонение определяется в тех же единицах, в каких изменяется варьирующий признак. Дисперсия и среднее квадратическое отклонение - меры абсолютной колеблемости:

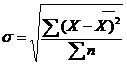 (11)
(11)
где σ - среднее квадратическое отклонение
Коэффициент вариации представляет собой отношение среднего квадратического отклонения к среднему ожидаемому значению и показывает степень отклонения получаемых результатов:
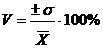 (12)
(12)
где
V - коэффициент вариации, %;
σ - среднее квадратическое отклонение;
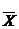 - среднее ожидаемое значение.
- среднее ожидаемое значение.
Так как коэффициент вариации - величина относительная, то на его размер не оказывают влияние абсолютные значения изучаемого показателя. С помощью коэффициента вариации можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется в пределах от 0 до 100%, при этом значение коэффициента прямо пропорционально силе колеблемости. Установлена следующая качественная оценка различных коэффициентов вариации:
до 10% - слабая колеблемость;
10-25 % - умеренная;
свыше 25% — высокая.
В качестве варианта может быть использован несколько упрощенный метод определения степени риска, Так как количественно риск характеризуется оценкой вероятной величины максимального и минимального результатов, то «чем больше диапазон между этими величинами при равной их вероятности, тем выше степень риска». Тогда для расчета дисперсии можно использовать следующую формулу:
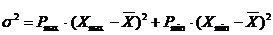 , (13)
, (13)
где
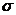 - дисперсия
- дисперсия
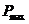 - вероятность получения максимального результата;
- вероятность получения максимального результата;
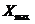 - максимальная величина результата;
- максимальная величина результата;
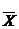 - средняя ожидаемая величина результата;
- средняя ожидаемая величина результата;
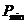 - вероятность получения минимального результата;
- вероятность получения минимального результата;
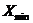 - минимальная величина результата.
- минимальная величина результата.
Полученные показатели следует учитывать в комплексе, так как использование отдельного критерия оценки риска не может служить основой принятия решения в пользу какой-либо стратегии.
В практике встречаются ситуации, когда отсутствует информация о вероятностях состояний среды, т.е. необходима оценка риска в условиях полной неопределенности. В таких случаях используются следующие критерии: максимакса, Вальда, Сэвиджа, Гурвица.
Критерий максимакса («все по максимуму») — критерий крайнего оптимизма (например, максимизация максимально возможной в определенных условиях прибыли предприятия). Выбирается та альтернатива, которая приведет к наилучшему результату в наиболее благоприятном случае.
Следует отметить, что ситуации, требующие применения такого критерия, в экономике, в общем, нередки, и пользуются им не только безоглядные оптимисты, но и игроки, поставленные в безвыходное положение, когда они вынуждены руководствоваться принципом «или пан, или пропал».
Критерий Вальда («рассчитывай на худшее») — критерий крайнего пессимизма — ориентирует лицо, принимающее решение, на решение, соответствующее выигрышу в наихудших условиях. Этот критерий еще называют правилом «наименьшего зла». В соответствии с критерием Вальда из всех самых неудачных результатов выбирается лучший. Это перестраховочная позиция, рассчитанная на худший случай. Такая стратегия приемлема, например, в случаях, когда игрок не столь заинтересован в крупной удаче, но хочет себя застраховать от неожиданных проигрышей. Выбор такой стратегии определяется отношением игрока к риску.
Критерий минимаксного риска Сэвиджа обеспечивает наименьшее значение максимальной величины риска. При этом минимизируются максимальные потери в результатах при принятии решений. Выбор стратегии аналогичен выбору стратегии по принципу Вальда с тем отличием, что игрок руководствуется не оценкой выигрышей, а оценкой рисков. В соответствии с критерием Сэвиджа выбирается минимально возможный из самых крупных рисков.
Критерий пессимизма-оптимизма Гурвица при выборе решения рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом.
Критерий Лапласа определяется средней величиной из возможных выигрышей и выбором решения, которому соответствует наибольшая средняя величина. Он представляет собой общую оценку всех событий, которые могут иметь хоть какое-то отношение к той или иной альтернативе.
Рассмотренные методы оценки риска по своей сути дают объективную оценку его вероятности и размеру возможного ущерба, но оперирование ими и полученными с их помощью характеристиками субъективно и зависит от восприятия риска и отношения к нему лица, принимающего решение.