КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
В РЭА несущими элементами конструкции часто являются пластины. Для расчета собственных (резонансных) колебаний необходимо привести к модели пластины элементы конструкций РЭА: стенки кожухов приборов, панели шасси, стенки экранов, печатные платы и т.д.
Пластиной является плоский элемент конструкции, длина и ширина которого во много раз больше толщины, а поверхность является плоскостью.
Из всех типов колебаний пластин наиболее вредны колебания в направлении минимальной жесткости. Печатная плата, закрепленная в приборе, в условиях вибрационных нагрузок (например, при транспортировке прибора автомобилем), обладает собственными частотами механических колебаний или конструктивными резонансами. Если частота вибрационных воздействий совпадает с собственной частотой печатной платы, она испытывает максимальные механические перегрузки, которые могут привести к ее разрушению, разрушению элементов, к отрыву контактных площадок, паяных контактов и проводов. Поэтому при проектировании РЭА возникает необходимость выполнения расчетов для определения вибрационной и ударной прочности конструкций, вычисления резонансных частот и нагрузок.
Для составления расчетных уравнений необходимо выбрать способ закрепления пластины в РЭА (граничные условия), в соответствии с Табл. 2., а затем, используя некоторые допущения и упрощения рассчитать требуемые параметры.
Существует три типа классических граничных условий:
· опертый край (обозначается на схеме пунктиром – – – –);
· защемленный край (обозначается на схеме штриховкой //////);
· свободный край (обозначается на схеме линией 
).
Практика показывает, что если край пластины задан с натягом, то такое закрепление считается защемленным. Кроме того, пластины могут быть закреплены в отдельных точках по периметру, например в четырех угловых точках. Пластина как система с распределенными параметрами, имеет бесконечное число резонансных частот. Наиболее опасен первый резонанс f0, так как он вызывает обычно максимальные перегрузки и амплитуды.
|
|
ОПРЕДЕЛНИЕ СОБСТВЕННОЙ ЧАСТОТЫКОЛЕБАНИЙ ПЕЧАТНОЙ ПЛАТЫ
Исходными данными для расчета собственной частоты колебаний печатной платы (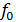
) являются:
a, b, h – геометрические размеры платы; a – большая сторона, м;
mP – масса платы, кг;
mЭ – масса элементов, установленных на плате, кг;
E – модуль упругости материала платы, Н/м2;
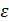– коэффициент Пуассона;
– плотность материала платы, кг/м3.
Для пластин с распределенной нагрузкой собственная частота колебаний вычисляется по формуле:
(1)
– коэффициент способа крепления пластины (см табл.2);
D – цилиндрическая жесткость пластины,
(2)
где Е – модуль упругости материала [Н/м2],
h – толщина пластины [м],
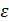– коэффициент Пуассона (Выбирается из Табл.1.).
m* – приведенная масса печатной платы.
(3)
где P – вес печатной платы [Н],
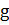– ускорение свободного падения ( 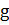= 9,81 м/с2);
mP – масса платы, кг;
mЭ – масса элементов, установленных на плате, кг;
Для пластин, закрепленных на втулках, с числом точек крепления n = 4,5,6; собственная частота колебаний определяется по формуле:
(4)
А – коэффициент, зависящий от количества точек крепления печатной платы:
при 
; 
при 
; 
при 
.
|
|