Лекция 15
Тема: Доверительный интервал. Доверительная вероятность
Цель: изучить понятие доверительного интервала, доверительной вероятности; научиться находить доверительный интервал с определенной надежностью на примере решения задачи.
План:
1. Понятие доверительного интервала, доверительной вероятности.
2. Построение доверительного интервала для генеральной средней и генеральной доли
3. Объем выборки
Литература: 1. Н.Ш. Кремер. Теория вероятностей и математическая статистика.
2. В.Е. Гмурман. Теория вероятностей и математическая статистика.
Понятие доверительного интервала, доверительной вероятности
Ранее мы рассматривали оценку параметров генеральной совокупности одним числом: т.е. 
- числом 
; р – числом w,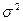 
- числом 
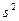или 
.Такие оценки называются точечными.
Однако в ряде задач требуется не только найти для параметра q подходящее численное значение, но и оценить его точность и надежность. Требуется знать — к каким ошибкам может привести замена параметра с его точечной оценкой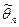 
и с какой степенью уверенности.ожидать, что эти ошибки не выйдут за известные пределы?
Такого рода задачи особенно актуальны при малом числе наблюдений, когда точечная оценка 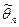в значительной мере случайна и приближенная замена q на 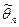может привести к серьезным ошибкам. Чтобы дать представление о точности и надежности оценки 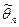, в математической статистике пользуются так называемыми доверительны ми интервалами и доверительными вероятностями.
Пусть для параметра q получена из опыта несмещенная оценка 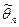. Оценим возможную при этом ошибку. Назначим некоторую достаточно большую вероятность γ (например, γ = 0,9, 0,98, 0,99) такую, что событие с вероятностьюγможно считать практически достоверным, и найдем такое числоe, для которого
;
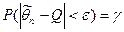
(1)
Равенство 1 означает, что с вероятностью γ неизвестное значение параметра q попадает в интервал 
, который называется доверительным, а вероятность γ- доверительной вероятностью.
При этом, ранее мы рассматривали вероятность попадания случайной величины в заданный неслучайный интервал. Здесь иначе: величина q - неслучайна, зато случаен доверительный интервал, его положение на оси абсцисс, случайна длина интервала 2e. Поэтому в данном случае говорят, что величина есть вероятность того, что случайный интервал покрывает точку q.
Наибольшее отклонение e оценки 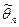от оцениваемого параметра q, которое возможно с заданной доверительной вероятностью γ, называется предельной ошибкой выборки.
Ошибки e называ ется ошибкой репрезентативности (представительства) выборки. Она возникает только вследствие того, что исследуется не вся совокупность, а лишь часть ее (выборка).
Построение доверительного интервала для генеральной средней и генеральной доли
Пусть случайная величина Х имеет нормальное распределение и известно ее среднее квадратическое отклонение 
. Требуется найти доверительный интервал, покрывающий математическое ожидание Мх ( 
) с надежностью γ, с учетом полученного значения.
Ранее было получено, что математическое ожидание выборочной средней равно 
; 
Будем считать, что вероятность попадания выборочного среднего в некоторую пока еще неизвестную e-окрестность математического ожидания и равна γ:
Как известно, для нормально распределенной случайной величины Х
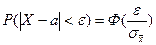- функция Лапласа в точке 
.
Учитывая то, что выборочное среднее, как среднее арифметическое нормально распределенных случайных величин Х1, Х2,….Хn распределено нормально, можно использовать данную формулу, только вместо 
взять среднее квадратическое отклонение выборочного среднего . Получаем:
, где 
(*)
Откуда 
Подставим данное выражение в левую часть формулы *
Получаем 
Или 
Доверительный интервал 
покрывает неизвестное генеральное среднее (мат. ожидание) с надежностью γ при известной дисперсии.
Пример: Случайная величина Х имеет нормальное распределение с известным средним квадратическим отклонением 
=3. Найти доверительный интервал для оценки неизвестного математического ожидания по выборочному среднему 
, если объем выборки n=36, а надежность оценки γ = 0,95.
Решение: Найдем сначала t: Ф(t) =0,95. по таблице функции Лапласа t= 1,96. Определим e: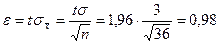 
Доверительный интервал запишется в виде: 
.
Доверительный интервал для математического ожидания при неизвестной дисперсии (и объема выборки меньше 30):
где s – «исправленное» выборочное среднее квадратическое отклонение, 
находится по распределению Стьюдента (по таблице по заданным n и γ).
Аналогично находится доверительный интервал для генеральной доли:
, где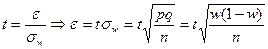 
Получаем 
Или 
Доверительный интервал 
покрывает неизвестную долю с надежностью γ.
Объем выборки
Для проведения выборочного наблюдения важным является установление объема выборки n, который в значительной степени определяет необходимые при этом временные, трудовые и стоимостные затраты. Для определения объема выборки необходимо задать надежность (доверительную вероятность) оценкиγи точность (предельную ошибку выборки) e.
, где s - дисперсия признака.
Отсюда
Выборка повторная Выборка бесповторная
Генеральная средняя 
Генеральная доля 
Если найден объем повторной выборки, то объем соответствующей бесповторной выборки
