Министерство науки и высшего образования
ФГОУ ВПО ПГУ
Политехнический институт
Факультет вычислительной техники
Кафедра: «Высшая и прикладная математика»
Реферат по теме «Теорема Бернулли»
по специальности «Теория вероятности и математическая статистика»
Выполнил: студент гр. 18ВБ1
Игумнова В.В.
Проверил: доцент, к.ф.-м.н.
Бойкова А. И.
Пенза, 2020
Закон больших чисел. Теорема Бернулли.
Возникновение теории вероятностей как науки относится к средним векам и первым попыткам математического анализа азартных игр, таких как кости и рулетка. Как показывает практика нельзя заранее предугадать, какое из допустимых значений примет случайная величина. Необходимо отметить, что о любой случайной величине мы располагаем определенными знаниями, но бывает очень тяжело найти закономерности в ее поведении.
Анализ соответствующей литературы показал, что при отдельных условиях суммарное поведение достаточно значительного числа случайных величин почти целиком теряет случайный характер и при этом делается закономерным.
На практике при изучении закономерностей массовых случайных явлений, зависящих от большого числа случайных факторов, мы используем так называемые предельные теоремы. К ним относятся теоремы Чебышева, Пуассона, Бернулли и т. д.
Предельные теоремы делятся на две группы. К первой группе относятся теоремы, объединенные под общим названием «закон больших чисел». В них ставятся условия, при которых среднее арифметическое случайных величин приближается к некоторым детерминированным (неслучайным) величинам.
Важный вклад в теорию «больших чисел» внёс Якоб Бернулли. Заслуга его заключается в том, что он дал доказательство закона больших чисел в простейшем случае независимых испытаний.
Необходимо отметить, что, заложенные Якобом Бернулли основы применения теории вероятностей в различных сферах жизни общества, в том числе и экономике, имели огромное значение. В его труде «Искусство предположений» ученый доказывает теорему о больших числах, выводит понятие доверительного интервала. Существует два вопроса, связанных с теорией вероятностей. Первый вопрос заключается в следующем: как будут соотноситься результаты, полученные на практике, с теоретическими? Второй вопрос состоит в решении обратной задачи: можно ли определить теоретическую вероятность по результатам испытаний?
Якоб Бернулли посвятил несколько десятилетий изучению этой задачи и математически доказал, что при бросании игрального кубика большое число раз доля случаев, когда выпадет четыре очка, будет приближаться к 1/6. Математик назвал свое открытие золотой теоремой, однако в современной формулировке она известна как закон больших чисел.
В 1713 году Бернулли изложил правила подсчёта вероятности для сложных событий и дал первый вариант «закона больших чисел», разъясняющего, почему частота события в серии испытаний не меняется хаотично, а в некотором смысле стремится к своему предельному теоретическому значению (то есть вероятности).
Закон больших чисел важен, поскольку он гарантирует устойчивость для средних значений некоторых случайных событий при достаточно длинной серии экспериментов.
Важно помнить, что закон применим только тогда, когда рассматривается большое количество испытаний.
Формулировка теоремы Бернулли:
Пусть производится п независимых испытаний, в каждом из которых вероятность появления события А равна р.
Теорема: Если в каждом из п независимых испытаний вероятность р появления события А постоянна, то как угодно близка к единице вероятность того, что отклонение относительной частоты от вероятности р по абсолютной величине будет сколь угодно малым, если число испытаний достаточно велико.
Другими словами, если ε - сколь угодно малое положительное число, то при соблюдении условий теоремы имеет место равенство:
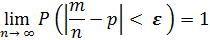
Теорема Бернулли состоит из двух частей, первая из которых говорит о том, что заданной точности можно достичь при конечном числе экспериментов. Вторая часть теоремы позволяет рассчитать количество экспериментов, которое потребуется для достижения желаемой точности.
Например, при проведении выборов в краевую государственную думу можно установить допустимое значение ошибки и определить число бюллетеней, которые должны будут заполнить избиратели, чтобы получить результат с заданной точностью.
Доказательство: Простое доказательство дано П.Л. Чебышевым как следствие из его же теоремы.
Обозначим через 
дискретную случайную величину — число появлений события в первом испытании, через 
— во втором, 
— в n -м испытании. Ясно, что каждая из величин может принять лишь два значения: 1 (событие A наступило) с вероятностью р и 0 (событие не появилось) с вероятностью 1 - p = q.
К рассматриваемым величинам можно применить теорему Чебышева, так как случайные величины попарно независимы и дисперсии их ограничены. Действительно, попарная независимость величин 
следует из того, что испытания независимы. Дисперсия любой величины 
(i = 1, 2,..., п) равна произведению pq; так как р + q = 1, то произведение pq не превышает 
и, следовательно, дисперсии всех величин ограничены, например, числом C = .
Применяя теорему Чебышева (частный случай) к рассматриваемым величинам, имеем:
Приняв во внимание, что математическое ожидание а каждой из величин 
(т.е. математическое ожидание числа появлений события в одном испытании) равно вероятности р наступления события, получим
Остается показать, что дробь 
равна относительной частоте т/п появлений события А в испытаниях. Действительно, каждая из величин 
при появлении события в соответствующем испытании принимает значение, равное единице; следовательно, сумма 
равна числу т появлений события в п испытаниях, а значит
Учитывая это равенство окончательно получим
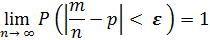
Замечание: Было бы неправильным на основании теоремы Бернулли сделать вывод, что с ростом числа испытаний относительная частота неуклонно стремится к вероятности р; другими словами, из теоремы Бернулли не вытекает равенство 
. В теореме речь идет лишьо вероятности того, что при достаточно большом числе испытаний относительная частота будет как угодно мало отличаться от постоянной вероятности появления события в каждом испытании.
Таким образом, сходимость относительной частоты m/n к вероятности р отличается от сходимости в смысле обычного анализа. Для того чтобы подчеркнуть это различие, вводят понятие «сходимости по вероятности». Точнее, различие между указанными видами сходимости состоит в следующем: если m/n стремится при 
к р как пределу в смысле обычного анализа, то начиная с некоторого n = N и для всех последующих значений n неуклонно выполняется неравенство |m/n – p|< 
; если же m/n стремится по вероятности к р при , то для отдельных значений n неравенство может не выполняться.
Итак, теорема Бернулли утверждает, что при относительная частота стремится по вероятности к р.
При доказательстве теоремы Бернулли получаем оценку:
Примеры:
Например, рассмотрим бросок шестигранной игральной кости, на которой с равной вероятностью может выпасть одно из чисел 1, 2, 3, 4, 5 или 6. Следовательно, математическое ожидание одного броска равно
{\displaystyle {\frac {1+2+3+4+5+6}{6}}=3{,}5}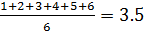 
Согласно закону больших чисел при большом количестве бросков их среднее значение, вероятно, будет близким к 3,5, при этом точность будет возрастать по мере увеличения числа бросков.
Из закона больших чисел следует, что эмпирическая вероятность успеха в серии испытаний Бернулли сходится к теоретической вероятности. Для случайной величины Бернулли математическое ожидание представляет собой теоретическую вероятность успеха, а среднее значение {\displaystyle n}n таких переменных (если они независимы и одинаково распределены) является относительной частотой.
Например, бросок правильной монеты — это испытание Бернулли. При одном броске теоретическая вероятность выпадения «орла» равна 1/2{\displaystyle 1/2}. Поэтому, согласно закону больших чисел, доля «орлов» при большом количестве испытаний «должна быть» примерно 1/2 {\displaystyle 1/2}. В частности, доля «орлов» после n {\displaystyle n} бросков сходится к 1/2{\displaystyle 1/2}, при {\displaystyle n\rightarrow \infty }.
Хотя доля орлов (и решек) стремится к {\displaystyle 1/2}1/2, почти наверное модуль разности количества орлов и решек станет большим, когда число бросков будет неограниченно возрастать. То есть при увеличении числа бросков вероятность того, что модуль разницы будет невелик, идет к нулю, а отношение модуля разницы к общему числу бросков почти наверное стремится к нулю.