Теоретический блок
Задание 1. В правом столбце таблицы представлены графики основных элементарных функций:  .
.
Заполните левый столбец таблицы соответствующими функциями.
Выполнение.
| Функции | Графики функций |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

| |

|
 Задание 2. Пользуясь графиком функции
Задание 2. Пользуясь графиком функции  , заполните таблицу:
, заполните таблицу:
Выполнение.

| |

| |
Пересечение с осью 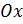
| |
Пересечение с осью 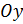
| |
| Промежутки убывания | |
| Промежутки возрастания | |

| |

|
Задание 3. Ниже представлены правила преобразований графиков. Рассмотрим функцию  Продолжите фразу:
Продолжите фразу:
Выполнение.
1. Чтобы построить график функции  , нужно график
, нужно график  сдвинуть вдоль оси __________ на ________ единиц ____________.
сдвинуть вдоль оси __________ на ________ единиц ____________.
2. Чтобы построить график функции 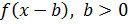 , нужно график
, нужно график  сдвинуть вдоль оси __________ на ________ единиц ____________.
сдвинуть вдоль оси __________ на ________ единиц ____________.
3. Чтобы построить график функции  , нужно график
, нужно график  сдвинуть вдоль оси __________ на ________ единиц ____________.
сдвинуть вдоль оси __________ на ________ единиц ____________.
4. Чтобы построить график функции  , нужно график
, нужно график  сдвинуть вдоль оси __________ на ________ единиц ____________.
сдвинуть вдоль оси __________ на ________ единиц ____________.
5. Чтобы построить график функции  , нужно график функции
, нужно график функции  сжать к оси _______ в
сжать к оси _______ в  раз.
раз.
6. Чтобы построить график функции  , нужно график функции
, нужно график функции  растянуть от оси _______ в
растянуть от оси _______ в  раз.
раз.
7. Чтобы построить график функции  , нужно график
, нужно график  отобразитьсимметрично относительно оси ___________.
отобразитьсимметрично относительно оси ___________.
8. Чтобы построить график функции  , нужно график
, нужно график  отобразитьсимметрично относительно оси ___________.
отобразитьсимметрично относительно оси ___________.
9. Чтобы построить график функции  , нужно график функции
, нужно график функции  растянуть вдоль оси ___________ в
растянуть вдоль оси ___________ в  раз.
раз.
10. Чтобы построить график функции  , нужно график функции
, нужно график функции  сжать вдоль оси _________ в
сжать вдоль оси _________ в  раз.
раз.
11. Чтобы построить график функции  , нужно построить график функции
, нужно построить график функции  , затем часть графика при
, затем часть графика при  сохранить, а при
сохранить, а при 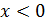 «сохранённую часть» графика ото бразить симметрично относительно оси ________.
«сохранённую часть» графика ото бразить симметрично относительно оси ________.
Практический блок
Задание 4. Начертите график какой-нибудь функции  , для которой:
, для которой:
а) 
б) 
в) 
Решение.
а)
б)
в)
Задание 5. Используя правила преобразования графиков, постройте в одной и той же системе координат графики следующих функций:
а)  ;
;
б)  ;
;
в)  ;
;
г)  .
.
Решение.
а)  ;
;
1. Графиком функции  является гипербола, ветви которой расположены в первой и третьей четвертях.
является гипербола, ветви которой расположены в первой и третьей четвертях.
2. Для того чтобы построить график функции  , необходимо сдвинуть вдоль оси
, необходимо сдвинуть вдоль оси 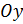 график
график  на 3 единицы вверх.
на 3 единицы вверх.
3. Для того чтобы построить график функции 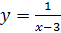 , необходимо сдвинуть вдоль оси
, необходимо сдвинуть вдоль оси 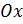 график
график  на 3 единицы вправо.
на 3 единицы вправо.

б)  .
.
1. Графиком функции  является парабола, с вершиной в начале координат и ветви которой опущены вниз.
является парабола, с вершиной в начале координат и ветви которой опущены вниз.
2. Для того чтобы построить график функции  , необходимо сдвинуть вдоль оси
, необходимо сдвинуть вдоль оси 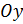 график
график  на 2 единицы вверх.
на 2 единицы вверх.
3. Для того чтобы построить график функции  , необходимо________________________________________________
, необходимо________________________________________________

в)  .
.
г)  .
.
Задание 6. Используя правила преобразования графиков, постройте графики следующих функций:
а)  ;
б) ;
б)  ;
в) ;
в) 
| г)  ;
д) ;
д)  . .
|
Решение.
а)  .
.
Для того чтобы построить график данной функции, необходимо:
1. Построить график гиперболы  .
.
2. Сдвинуть  на 4 единицы влево по оси
на 4 единицы влево по оси 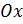 , получим график
, получим график 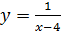 .
.
3. Растянуть график 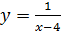 вдоль оси
вдоль оси 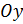 в 3 раза, в результате получим искомый график функции
в 3 раза, в результате получим искомый график функции  .
.

б)  .
.
в)  .
.
г) 
Задание 7. Построить график следующих функций:
а)  ;
б) ;
б)  ;
в) ;
в)  ; ;
| г)  ;
д) ;
д)  ;
е) ;
е) 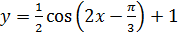 . .
|
Решение.
Общая схема построения графика функции с помощью геометрических преобразований.
Для построения некоторых функций необходимо применить комбинацию приемов, рассмотренных в примерах №5-6. В этом случае необходимо последовательно применять преобразования графика, так что построение графика исходной функции свелось к построению одной из простейших элементарных функций. Очевидно, что если функция будет иметь вид  , то это поможет определить вид преобразования, что упростит построение. Именно поэтому, перед построением графика функции, ее целесообразно привести к виду
, то это поможет определить вид преобразования, что упростит построение. Именно поэтому, перед построением графика функции, ее целесообразно привести к виду 
а) 
На первом шаге необходимо представить исходную функцию в виде  . Для этого применим метод выделения полного квадрата.
. Для этого применим метод выделения полного квадрата.
1. Коэффициенты при  вынесем за скобку:
вынесем за скобку:  .
.
2. Выделим в скобке квадрат суммы 

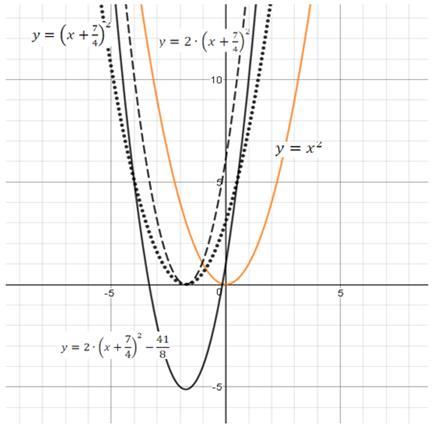
3. Строим параболу  , которую:
, которую:
Сдвигаем  вдоль оси
вдоль оси 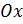 на
на  единиц влево, получим график
единиц влево, получим график  .
.
Растягиваем график  вдоль оси
вдоль оси 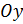 в 2 раза, получим график
в 2 раза, получим график  .
.
Сдвигаем  вдоль оси
вдоль оси 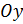 на
на 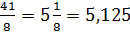 единиц вниз, получим график исходной функции
единиц вниз, получим график исходной функции 
б)  .
.
в)  .
.
1. На первом шаге необходимо представить исходную функцию в виде  .
.
 .
.
2. Строим график функции  .
.
Сдвигаем 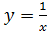 влево на 1 единицу вдоль оси
влево на 1 единицу вдоль оси 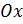 , получаем
, получаем  .
.
Растянуть график  вдоль оси
вдоль оси 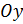 в 4 раза, таким образом, получим график функции
в 4 раза, таким образом, получим график функции  .
.
Отобразим  симметрично относительно оси абсцисс, получим
симметрично относительно оси абсцисс, получим  .
.
Сдвигаем  вдоль оси
вдоль оси 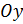 на 6 единиц вверх, получим график исходной функции
на 6 единиц вверх, получим график исходной функции  .
.
3. Построим график:
г)  .
.
д)  .
.
1. Представить исходную функцию в виде  .
.

2. Строим 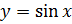 .
.
е) 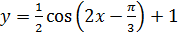 .
.