Схема и формула Бернулли.

Сложение и умножение событий.

Суммой 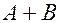двух событий и называется событие, состоящее в появлении или события , или события , или обоих вместе. Суммой нескольких событий называется событие, которое состоит в появлении хотя бы одного из этих событий.

Теорема сложения вероятностей для несовместных событий:

Если события и несовместны, то . Эта теорема обобщается на любое конечное число событий:

Если события попарно несовместны, то

.

Произведением двух событий и называется событие, состоящее в совместном появлении этих событий.

Теорема умножения вероятностей:

где - условная вероятность события , вычисленная в предположении, что событие уже наступило. Условную вероятность еще обозначают P (A/B).

Для независимых событий

Теорема сложения вероятностей для произвольных событий:

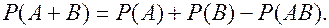
Задача 7.

Два стрелка стреляют по мишени. Вероятности попадания в мишень для первого и второго стрелка соответственно равны 0,7 и 0,5. Найти вероятность того, что:

1) оба стрелка попадут в мишень;

Хотя бы один из стрелков попадет в мишень.

Решение. Введем события:

- первый стрелок попал в мишень;

- второй стрелок попал в мишень.

По условию

- оба стрелка попали в мишень;

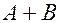- хотя бы один стрелок попал в мишень.

События и , очевидно, независимы. Поэтому

По теореме сложения вероятностей:

Задача 8. Известно, что в некоторой местности в июле 2006 г. наблюдалось шесть пасмурных дней. Найти вероятность того, что первого и второго июля была ясная погода.

Решение. Введем обозначения событий:

- первого июля был ясный день;

- второго июля был ясный день.

В июле 31 день. Число ясных дней в указанной местности в июле 2006 г.

Вероятность того, что второго июля был ясный день, при условии, что первого был ясный день, т. е. условная вероятность события :

Искомая вероятность того, что оба дня были ясными, по теореме умножения вероятностей равна:

Формула полной вероятности.

Пусть событию А предшествует одно из событий H ₁, H ₂ , …, H_n (n ³ 2), которые образуют полную группу.

Тогда верна формула полной вероятности:

События H ₁, H ₂ , …, H_n называются гипотезами, и событие А может произойти только с одной из гипотез.

Задача 9.

В магазин поступили однотипные телевизоры с 1-го завода 10 шт., со 2-го завода 15 шт. Вероятность изготовить бракованный телевизор на 1-м заводе равна 0,1, на 2-м – 0,2. Случайно отобрали один из поступивших телевизоров. Какова вероятность того, что он бракованный?

Решение.

Введем события:

А – «Выбранный телевизор оказался бракованным»,

Н ₁– «Выбранный телевизор изготовлен на 1-м заводе»,

Н ₂– «Выбранный телевизор изготовлен на 2-м заводе»,

Гипотезы Н ₁, Н ₂ несовместны и событие А может произойти только с одним из них. Значит можно применить формулу полной вероятности.

P(Н ₁)=10/25 = 2/5=0,4; P(A/ Н ₁) = 0,1;

P(Н ₂)=15/25 = 3/5=0,6; P(A/ Н ₂) = 0,2.

Формула Байеса.

При выполнении для гипотез H ₁, H ₂ , …, H_n и события А п. 6. верна формула Байеса:

, i = 1, …, n.

По этим формулам вычисляются так называемые апостериорные вероятности гипотез, то есть вероятности гипотез после того как событие А произошло. Безусловные вероятности гипотез Р (Н_i) называются априорными.

Задача 10.

При условиях задачи 9 найти вероятность гипотез Н ₁, Н ₂ ,если известно, что отобранный телевизор оказался бракованным.

Решение.

Используя результаты вычислений из решения задачи 9, по формуле Байеса имеем:

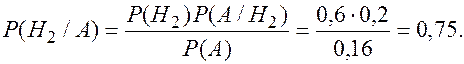
Как видим, апостериорная вероятность гипотезы Н ₁ уменьшилась по сравнению априорной вероятностью. Объяснение простое: поскольку на первом заводе брака делается в два раза меньше, чем на втором, а выбранный телевизор оказался бракованным, то, естественно, вероятность того, что он из 1-го завода уменьшится.

Схема и формула Бернулли.