Окружность — геометрическая фигура на плоскости, все точки которой равноудалены от данной точки (центра окружности). 
Радиус окружности — расстояние от центра окружности до любой из её точек. Также радиусом окружности называется отрезок, соединяющий центр окружности с одной из точек окружности.
Диаметр окружности — отрезок, соединяющий две точки окружности и проходящий через её центр. Также диаметром называется длина этого отрезка. Величина диаметра окружности равна удвоенной величине её радиуса.
Хорда — отрезок, соединяющий две точки окружности.
- Серединный перпендикуляр к хорде проходит через центр окружности.
- Радиус, перпендикулярный хорде, делит её пополам.
- Равные хорды стягивают равные дуги.
Дуга окружности. Любые две несовпадающие точки окружности делят её на две части, каждая из которых называется дугой окружности. Данные точки называются концами этих дуг.
Если отрезок, соединяющий концы дуги является диаметром, то такая дуга называется полуокружностью.

Центральный угол — угол с вершиной в центре окружности.
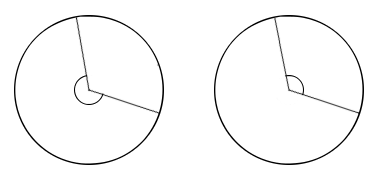
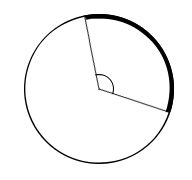
Угловая мера дуги АВ (градусная или радианная), лежащей внутри центрального угла АОВ равна угловой мере (градусной или радианной) центрального угла АОВ.
Вписанный угол — угол, вершина которого лежит на окружности, а стороны пересекают окружность.
- Угловая мера вписанного угла равна половине угловой меры дуги окружности, на которую он опирается.
- Угловая мера вписанного угла равна половине угловой меры центрального угла, опирающегося на ту же дугу.
- Вписанные углы, опирающиеся на одну и ту же дугу, равны.
- Вписанный угол, опирающийся на полуокружность, прямой.
Секущая — прямая, проходящая через две различные точки окружности.
Касательная — прямая, имеющая с окружностью ровно одну общую точку. Эта точка называется точкой касания.
- Касательная к окружности перпендикулярна к радиусу, проведённому в точку касания.
- Отрезки касательных к окружности, проведённые из одной точки, равны.
Вписанная в многоугольник окружность — окружность, лежащая внутри многоугольника и касающаяся всех его сторон.
Многоугольник в этом случае называется описанным около окружности.
Центр вписанной окружности — точка пересечения биссектрис углов многоугольника.
· В любой треугольник можно вписать окружность.
· В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
· В любой правильный многоугольник можно вписать окружность.
Описанная около многоугольника окружность — окружность, содержащая все вершины многоугольника.
Центр описанной окружности — точка пересечения серединных перпендикуляров к сторонам многоугольника.
· Около любого треугольника можно описать окружность.
· Около четырехугольника можно описать окружность тогда и только тогда, когда сумма его противоположных углов равна 180o.
· Около параллелограмма можно описать окружность тогда и только тогда, когда он является прямоугольником.
· Около трапеции можно описать окружность тогда и только тогда, когда трапеция равнобедренная.
· Около любого правильного многоугольника можно описать окружность.