1. На рисунке изображён график функции y = f (x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику функции или её производной.
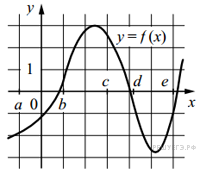
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ | |
| А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) | 1) производная отрицательна на всём интервале 2) производная положительна на всем интервале 3) функция отрицательна на всем интервале 4) функция положительна на всём интервале |
2. На рисунке точками изображено число родившихся мальчиков и девочек за каждый календарный месяц 2013 года в городском роддоме. По горизонтали указываются месяцы, по вертикали — количество родившихся мальчиков и девочек (по отдельности). Для наглядности точки соединены линиями.
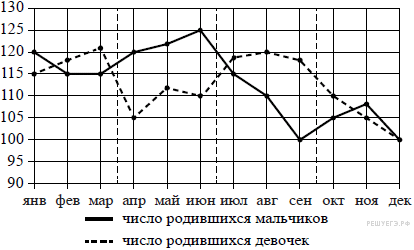
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику рождаемости в этот период.
| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ РОЖДАЕМОСТИ | |
| А) 1-й квартал года Б) 2-й квартал года В) 3-й квартал года Г) 4-й квартал года | 1) рождаемость мальчиков в течение 2-го и 3-го месяцев периода была одинаковой 2) рождаемость девочек снижалась 3) в каждом месяце девочек рождалось больше, чем мальчиков 4) каждом месяце мальчиков рождалось больше, чем девочек |
3. На диаграмме изображён среднемесячный курс евро в период с октября 2013 года по сентябрь 2014 года. По горизонтали указываются месяц и год, по вертикали — курс евро в рублях.
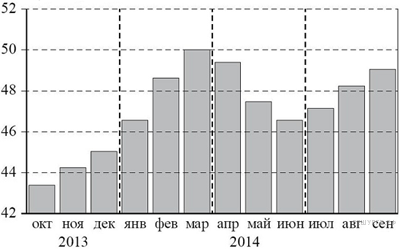
| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ КУРСА ЕВРО | |
| А) октябрь−декабрь 2013г. Б) январь–март 2014г. В) апрель–июнь 2014г. Г) июль–сентябрь 2014. | 1) содержит месяц с наибольшим курсом евро за период с октября 2013 года по сентябрь 2014 года 2) содержит месяц с наименьшим курсом евро за период с октября 2013 года по сентябрь 2014 года 3) среднемесячный курс евро падал все месяцы периода 4) в последний месяц периода средний курс евро был больше 48 рублей и меньше 50 рублей за 1 евро |
4. Больному прописано лекарство, которое нужно принимать по 0,5 г 2 раза в день в течение 7 дней. В одной упаковке 10 таблеток по 0,25г. Какого наименьшего количества упаковок хватит на весь курс лечения?
5. На графике изображена зависимость скорости движения рейсового автобуса на маршруте между двумя городами от времени. На вертикальной оси отмечена скорость в км/ч, на горизонтальной — время в часах, прошедшее с начала движения автобуса.
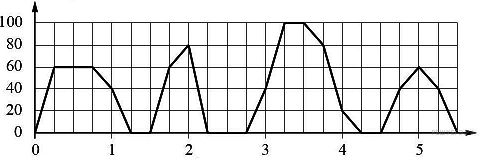
Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику движения автобуса на этом интервале.
| ИНТЕРВАЛЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ ДВИЖЕНИЯ | |
| А) первый час пути Б) второй час пути В) третий час пути Г) четвертый час пути | 1) была остановка длительностью 30 минут 2) скорость автобуса не опускалась ниже 20 км/ч 3) скорость автобуса не превышала 60 км/ч 4) была остановка длительностью 15 минут |
6. На графике показана зависимость крутящего момента автомобильного двигателя от числа его оборотов в минуту. На оси абсцисс откладывается число оборотов в минуту. На оси ординат — крутящий момент в H · м.
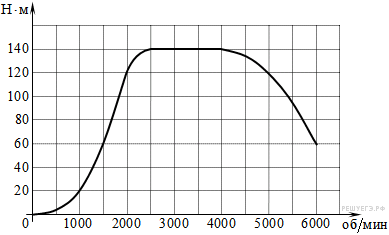
Пользуясь графиком, поставьте в соответствие каждому интервалу количества оборотов двигателя характеристику зависимости крутящего момента двигателя на этом интервале.
| ХАРАКТЕРИСТИКИ ПРОЦЕССА | ИНТЕРВАЛЫОБОРОТОВ | |
| А) крутящий момент не менялся Б) крутящий момент падал В) крутящий момент рос быстрее всего Г) крутящий момент не превышал 60 H · м | 1) 0 − 1500 об/мин. 2) 1500 − 2000 об/мин. 3) 2500 − 4000 об/мин. 4) 4000 − 6000 об/мин. |
7. На рисунке изображён график функции y = f (x). Числа a, b, c, d и e задают на оси x четыре интервала. Пользуясь графиком, поставьте в cоответствие каждому интервалу характеристику функции или её производной.
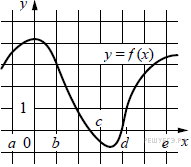
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | ЗНАЧЕНИЯ ПРОИЗВОДНОЙ | |
| А) (a; b) Б) (b; c) В) (c; d) Г) (d; e) | 1) производная отрицательна на всём интервале 2) производная положительна в начале интервала и отрицательна в конце интервала 3) функция отрицательна в начале интервала и положительна в конце интервала 4) производная положительна на всём интервале |
8. На рисунке точками показаны объёмы месячных продаж обогревателей в магазине бытовой техники. По горизонтали указываются месяцы, по вертикали — количество проданных обогревателей. Для наглядности точки соединены линией.
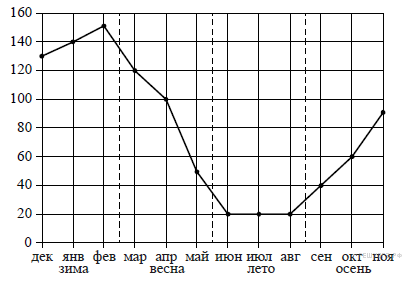
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику продаж обогревателей.
| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ | |
| А) зима Б) весна В) лето Г) осень | 1) Ежемесячный объём продаж рос, но был меньше 100 штук. 2) Ежемесячный объём продаж падал. 3) Ежемесячный объём продаж рос и был больше 120 штук. 4) Ежемесячный объём продаж не менялся в течение всего периода. |
9. На рисунке точками показано атмосферное давление в городе N на протяжении трёх суток с 4 по 6 апреля 2013 года. В течение суток давление измеряется 4 раза: в 0:00, в 6:00, в 12:00 и в 18:00. По горизонтали указывается время суток и дата, по вертикали — давление в миллиметрах ртутного столба. Для наглядности точки соединены линиями.
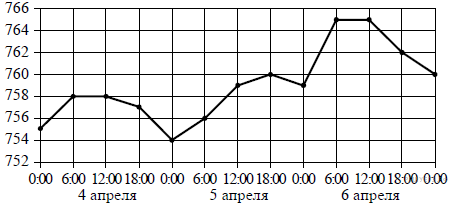
Пользуясь рисунком, поставьте в соответствие каждому из указанных периодов времени характеристику атмосферного давления в городе N в течение этого периода.
| ПЕРИОДЫВРЕМЕНИ | ХАРАКТЕРИСТИКИ | |
| А) вечер 4 апреля (с 18 до 0 часов) Б) день 5 апреля (с 12 до 18 часов) В) ночь 6 апреля (с 0 до 6 часов) Г) утро 6 апреля (с 6 до 12 часов) | 1) давление не изменилось 2) наибольший рост давления 3) давление росло, но не превышало 760 мм рт. ст. 4) давление падало |
10. На рисунке изображён график функции y = f (x) и отмечены точки K, L, M и N на оси x. Пользуясь графиком, поставьте в соответствие каждой точке характеристику функции и её производной.
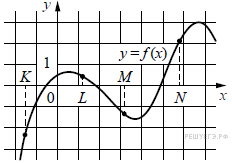
Ниже указаны значения производной в данных точках. Пользуясь графиком, поставьте в соответствие каждой точке значение производной в ней.
| ТОЧКИ | ХАРАКТЕРИСТИКИ ФУНКЦИИ ИЛИ ПРОИЗВОДНОЙ | |
| А) K Б) L В) M Г) N | 1) Функция положительна, производная отрицательна. 2) Функция отрицательна, производная отрицательна. 3) Функция отрицательна, производная положительна. 4) Функция положительна, производная положительна. |
Задание №15. Задачи по планиметрии.
1. Гипотенуза прямоугольного треугольника равна 26. Один из его катетов равен 10. Найдите другой катет.
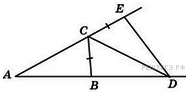
2. В треугольнике 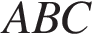 угол
угол  равен
равен  , угол
, угол 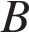 равен
равен  ,
, 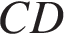 – биссектриса внешнего угла при вершине
– биссектриса внешнего угла при вершине 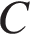 , причем точка
, причем точка 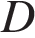 лежит на прямой
лежит на прямой 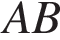 . На продолжении стороны
. На продолжении стороны 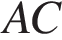 за точку
за точку 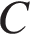 выбрана такая точка
выбрана такая точка 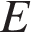 , что
, что  . Найдите угол
. Найдите угол  . Ответ дайте в градусах
. Ответ дайте в градусах
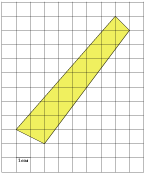
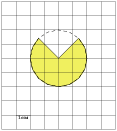
3. Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки
1 см  1 см (см. рис.). В ответе запишите
1 см (см. рис.). В ответе запишите  .
.
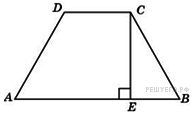
4. Основания равнобедренной трапеции равны 7 и 51. Тангенс острого угла равен  . Найдите высоту трапеции.
. Найдите высоту трапеции.
5. Найдите тупой угол параллелограмма, если его острый угол равен  . Ответ дайте в градусах.
. Ответ дайте в градусах.
6. В треугольнике 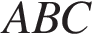 угол
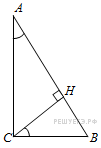
угол  равен 90°, высота
равен 90°, высота  равна 4,
равна 4,  . Найдите
. Найдите  .
. 
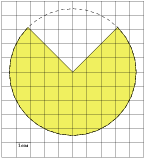
7. Найдите (в см2) площадь S закрашенной фигуры, изображенной на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). В ответе запишите
1 см (см. рис.). В ответе запишите  .
.
8. В треугольнике  угол
угол 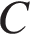 равен 90°, косинус внешнего угла при вершине
равен 90°, косинус внешнего угла при вершине  равен
равен 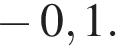 Найдите
Найдите  .
.
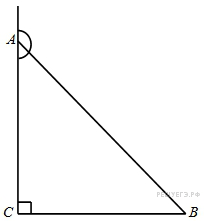
9. В треугольнике 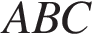 угол
угол 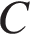 равен 90°, синус внешнего угла при вершине
равен 90°, синус внешнего угла при вершине  равен
равен 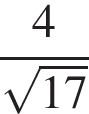 . Найдите
. Найдите 

10. Найдите площадь четырехугольника, изображенного на клетчатой бумаге с размером клетки 1 см  1 см (см. рис.). Ответ дайте в квадратных сантиметрах.
1 см (см. рис.). Ответ дайте в квадратных сантиметрах.