Интегральное и дифференциальное исчисление

Министерство Российской Федерации

По делам гражданской обороны, чрезвычайным ситуациям

И ликвидации последствий стихийных бедствий

Академия гражданской защиты

Кафедра системного анализа и управления

Гальченко В. Т., Бахтиярова О.Н.

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

ПО ИЗУЧЕНИЮ ДИСЦИПЛИНЫ

«ВЫСШАЯ МАТЕМАТИКА»

Химки - 2018

УДК 517.91

ББК 22. 161.6

Г 17

Авторы: Гальченко В. Т., Бахтиярова О.Н,.

Гальченко В.Т. Методические указания по изучению дисциплины «Математика» В.Т. Гальченко, О.Н. Бахтиярова. – Химки: АГЗ МЧС России, 2018 – 88 с.

Настоящие методические указания разработаны в соответствии с учебной программой дисциплины «Математика» и предназначены для студентов заочного факультета, обучающихся по специальности «Пожарная безопасность».

В методических указаниях даны рекомендации по научной организации самостоятельной работы обучающихся при изучении дисциплины, изложены основные цели изучения дисциплины, требования к студентам по её изучению, тематический план и содержание учебных занятий, задания домашней контрольной работы, вопросы для подготовки к экзамену, основная и дополнительная литература для изучения дисциплины.

Компьютерный набор: Гальченко В. Т., Бахтиярова О.Н.

© АГЗ МЧС России, 2018

ВВЕДЕНИЕ

Общей задачей дисциплины является приобретение студентами знаний об основных понятиях и методах высшей математики; формирование современного математического мышления; выработка приемов и навыков решения конкретных задач высшей математики; формирование навыков математического исследования аналитического, численного и прикладного характеров; освоение методов математической формализации различных процессов и явлений; обучению анализу полученных решений.

Главная задача обучения состоит в освоении дисциплины студентами заочного факультета по специальности «Пожарная безопасность» на уровне, позволяющем достаточно квалифицированно выполнять работы в области математического обеспечения, моделирования, прогнозирования и оптимального управления применительно к конкретным задачам инженерной и научной практики поисково-спасательных служб и сил РСЧС.

В результате изучения дисциплины студенты должны:

знать:

_ основные положения теории высшей математики;

. _. аналитические подходы и математические методы решения базовых

задач;

- математические методы решения прикладных задач и научно

исследовательских задач.

уметь:

- использовать в своей практической деятельности возможности

вычислительной техники, современные математические методы;

- выбирать наиболее подходящие математические методы к анализу

задач, возникающих в практике МЧС.

- формулировать и ставить задачи теоретического и прикладного

характера;

При изучении дисциплины особое внимание уделяется выработке навыков в использовании полученных знаний при решении прикладных задач и научно-исследовательских задач

владеть:

- навыками решения задач по следующим разделам:

а) элементы линейной алгебры;

б) элементы векторной алгебры;

в) аналитической геометрии;

г) пределы и производная функции;

д) исследование функций с помощью производной;

е) комплексные числа и многочлены;

ж) неопределенный интеграл;

з) определенный интеграл;

и) функции многих переменных;

к) кратные и криволинейные интегралы;

математическим аппаратом в исследовательской, расчётно-конструкторской и оперативно-тактической практике специалиста в различных чрезвычайных ситуациях мирного и военного времени.

IV. ЗАДАНИЯ ДОМАШНЕЙ КОНТРОЛЬНОЙ РАБОТЫ

Примечание. Номер варианта N заданий домашней контрольной работы соответствует номеру по порядку студента в классном журнале учёта успеваемости.

Линейная алгебра и аналитическая геометрия

Вариант № 1

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ).

1. Найти матрицу С = - 3В, где А = ; В =

2. Найти решение матричного уравнения ХА=В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,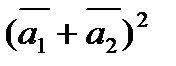

где = 3; = 4; угол между векторами и

4. Даны векторы (4; 2; -4) и (6; -3;2).

Вычислить

а) ;

б) .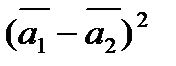

5. Даны векторы (3; -1; 2) и (1; 2;-1).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (4;5) и В (-1; 7).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 2

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = - 3В, где А = ; В =

2. Найти решение матричного уравнения XА = В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,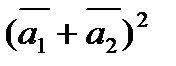

где = 3; = 4; угол между векторами и

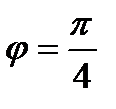
4. Даны векторы (4; 2; -4) и (6; -3;2).

Вычислить

а) ;

б) .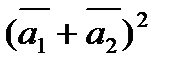

5. Даны векторы (3; -4; 2) и (0; 2;-1).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (5;-9) и В (3; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 3

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = А - 4 , где А = ; В =

2.Найти решение матричного уравнения ХА=В, имеющего вид:

Х 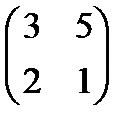= и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 3; = 4; угол между векторами и

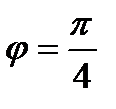
4. Даны векторы (4; 2; -4) и (6; -3;2).

Вычислить

а) ;

б) .

5. Даны векторы (1; -4; 1) и (7; 2;-8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (2;-6) и В (7; 0).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 4

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = А - 4 , где А = ; В =

2.Найти решение матричного уравнения АХ=В, имеющего вид:

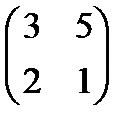Х = и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 2; = 4; угол между векторами и

4. Даны векторы (4; 2; -4) и (6; -3;0).

Вычислить

а) ;

б) .

5. Даны векторы (1; -1; 1) и (5; 2;-8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (-3;-3) и В (1; 2).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 5

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2. Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,

где = 2; = 4; угол между векторами и

4. Даны векторы (4; 2; -4) и (4; -3;2).

Вычислить

а) ;

б) .

5. Даны векторы (1; -1; 4) и (5; -2;8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В (2; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 6

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2.Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 3; = 4; угол между векторами и

4. Даны векторы (4; 0; -4) и (6; -3;5).

Вычислить

а) ;

б) .

5. Даны векторы (1; -4; 1) и (5; 2;-8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (8;-7) и В (4; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 7

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2.Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 2; = 4; угол между векторами и

4. Даны векторы (4; 2; -4) и (6; -3;0).

Вычислить

а) ;

б) .

5. Даны векторы (1; -1; 1) и (5; 2;-8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-8) и В (5; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 8

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2. Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 2; = 4; угол между векторами и

4. Даны векторы (4; 2; -4) и (6; -3;0).

Вычислить

а) ;

б) .

5. Даны векторы (1; -1; 1) и (4; 1;-3).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (3;-6) и В (6; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 9

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ). Множества

1. Найти матрицу С = – 4В, где А = ; В =

2. Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,

где = 2; = 4; угол между векторами и

4. Даны векторы (4; 2; -4) и (6; -3;0).

Вычислить

а) ;

б) .

5. Даны векторы (1; -1; 1) и (4; 1;-3).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (3;-8) и В (-2; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

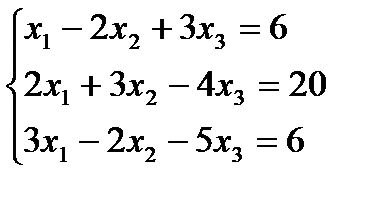
Вариант № 10

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = А - 4 , где А = ; В =

2.Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,

где = 2; = 5; угол между векторами и

4. Даны векторы (4; 2; -4) и (6; -3;2).

Вычислить

а) ;

б) .

5. Даны векторы (1; -4; 1) и (7; 2;-8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (-5;-5) и В (8; 1).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 11

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ).

1. Найти матрицу С = - 3В, где А = ; В =

2. Найти решение матричного уравнения ХА=В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,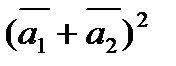

где = 4; = 4; угол между векторами и

4. Даны векторы (5; 2; -5) и (3; -3;2).

Вычислить

а) ;

б) .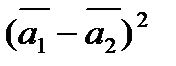

5. Даны векторы (0; -1; -2) и (1; 2;-4).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (4;3) и В (-1; 1).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 12

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = - 3В, где А = ; В =

2. Найти решение матричного уравнения XА = В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,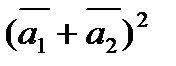

где = 5; = 4; угол между векторами и

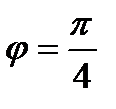
4. Даны векторы (3; 2; -3) и (2; -3;2).

Вычислить

а) ;

б) .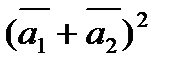

5. Даны векторы (3; 0; 2) и (0; 2;-2).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (3;-4) и В (3; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант №1 3

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = А - 4 , где А = ; В =

2.Найти решение матричного уравнения ХА=В, имеющего вид:

Х 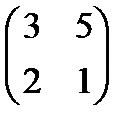= и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 2; = 4; угол между векторами и

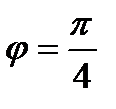
4. Даны векторы (5; 2; -1) и (6; -1;2).

Вычислить

а) ;

б) .

5. Даны векторы (1; -4; 1) и (6; -2;-1).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (2;-2) и В (5; 0).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 1 4

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = А - 4 , где А = ; В =

2.Найти решение матричного уравнения АХ=В, имеющего вид:

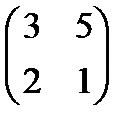Х = и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 1; = 4; угол между векторами и

4. Даны векторы (4; 2; -4) и (6; -3;1).

Вычислить

а) ;

б) .

5. Даны векторы (2; -1; 2) и (5; 2;-0).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (-3;-1) и В (2; 2).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 1 5

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2. Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3. Вычислить:

а) ;

б) ,

где = 1; = 6; угол между векторами и

4. Даны векторы (3; 2; -3) и (1; -3;1).

Вычислить

а) ;

б) .

5. Даны векторы (1; -1; 2) и (5; -3;8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (3;-2) и В (2; -3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 16

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2.Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 3; = 4; угол между векторами и

4. Даны векторы (2; 1; -2) и (5; -3;5).

Вычислить

а) ;

б) .

5. Даны векторы (1; -1; 1) и (5; 2;-0).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (8;-7) и В (4; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 17

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2.Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3.Вычислить:

а) ;

б) ,

где = 2; = 4; угол между векторами и

4. Даны векторы (4; 2; -2) и (6; -3;1).

Вычислить

а) ;

б) .

5. Даны векторы (1; -2; 1) и (5; 0;-8).

Вычислить векторное произведение:

а) ;

б) .

в) найти модуль векторного произведения

6. Составить и построить уравнения прямой, проходящей через две точки А (-2;-2) и В (5; 3).

7. Решить систему линейных алгебраических уравнений методом Гаусса, правилом Крамера, с помощью обратной матрицы.

Вариант № 18

Матрицы. Определители. Векторная алгебра. Системы линейных алгебраических уравнений (СЛАУ)).

1. Найти матрицу С = – 4В, где А = ; В =

2. Найти решение матричного уравнения АХ=В, имеющего вид:

Х = и сделать проверку.

3.Вычислить:

а) ;

б)

Поиск по сайту: