Первый закон термодинамики, которой отображает обмен энергией между системой и окружающей средой в форме работы и теплоты. Это одни из видов законов сохранения энергии.
Закон Гесса для химических реакций говорит о том, что: величина теплового эффекта изобарных или изохорных процессов зависит только от начального и конечного состояний системы и не зависит от хода процесса.
Закон Гесса применяют для вычисления тепловых эффектов химических реакций.
Закон Гесса имеет полезные следствия:
1. Энтальпия химической реакции при стандартных условиях равна разности алгебраической суммы энтальпий возникновения продуктов реакции, и суммы энтальпий образования исходных веществ.
2. Теплота, которая выделяется при горении вещества в кислороде в количестве 1 моль до образования высших оксидов при стандартных условиях, называется стандартной теплотой сгорания вещества. Энтальпия реакции горения равна разности суммы энтальпий (с учетом знаков) сгорания исходных веществ и суммы энтальпий горения продуктов реакции при учете их стехиометрических коэффициентов. По закону Гесса количество выделяемой теплоты при окислении не зависит от того как и где происходит процесс горения, если продукты реакции не изменяются.
3. При разложении вещества расходуется (требуется) такое же по модулю количество теплоты как при образовании данного вещества. Это закон Лавуазье – Лапласа.
4. Если повести две реакции, которые приводят из разных начальных состояний к одним конечным состояниям, то разница в тепловых эффектах составит количество теплоты перехода из первого начального состояния во второе.
5. При проведении двух реакций из одних начальных состояний в различные конечные состояния разница в тепловых эффектах составит тепловой эффект перехода от первого конечного состояния во второе.
Второй закон термодинамики говорит о направлении протекания процессов. Все самопроизвольные процессы происходят так, что система стремится к минимуму энергии, при этом энтропия системы увеличивается.
38 Внутренняя энергия
Энергия представляет собой общую меру различных форм движения материи. Соответственно формам движения материи различают и виды энергии – механическую, электрическую, химическую и т.д. Всякая термодинамическая система в любом состоянии обладает некоторым запасом энергии, существование которой было доказано Р.Клаузиусом (1850) и получило название внутренней энергии.
Внутренняя энергия (U) – это энергия всех видов движения микрочастиц, составляющих систему, и энергия их взаимодействия между собой.
Внутренняя энергия складывается из энергии поступательного, вращательного и колебательного движения частиц, энергии межмолекулярного и внутримолекулярного, внутриатомного и внутриядерного взаимодействий и др.
Энергию внутримолекулярного взаимодействия, т.е. энергию взаимодействия атомов в молекуле, часто называют химической энергией. Изменение этой энергии имеет место при химических превращениях.
Для термодинамического анализа нет необходимости знать из каких форм движения материи складывается внутренняя энергия.
Запас внутренней энергии зависит только от состояния системы. Следовательно, внутреннюю энергию можно рассматривать как одну их характеристик этого состояния наравне с такими величинами, как, давление, температура.
Каждому состоянию системы соответствует строго определенное значение каждого из его свойств.
Если гомогенная система в начальном состоянии имеет объем V1, давление P1, температуру T1, внутреннюю энергию U1, удельную электропроводностьæ1и т.д., а в конечном состоянии эти свойства соответственно равны V2, P2, T2, U2, æ2и т.д., то изменение каждого свойства при переходе системы из начального состояния в конечное будет одним и тем же, независимо от того, каким путем переходит система из одного состояния в другое: первым, вторым или третьим (рис. 1.4).
Рис. 1.4 Независимость свойств системы от пути ее перехода
из обычного состояния в другое
Т.е. (U2 - U1)I = (U2 - U1)II = (U2 - U1)III (1.4)
Где цифры I, II, III и т.д. указывают пути процесса. Следовательно, если система из начального состояния (1) в конечное (2) перейдет по одному пути, а из конечного в начале – по другому пути, т.е. совершится круговой процесс (цикл), то изменение каждого свойства системы будет равно нулю.
Таким образом, изменение функции состояния системы не зависит от пути процесса, а зависит лишь от начального и конечного состояний системы. Бесконечно малое изменение свойств системы обозначается обычно знаком дифференциала d. Например, dU– бесконечное малое изменение внутренней энергии и т.д.
Формы обмена энергией
В соответствии с различными формами движения материи и различными видами энергии существуют различные формы обмена энергией (передача энергии) – формы взаимодействия. В термодинамике рассматриваются две формы обмена энергии между системой и окружающей средой. Это работа и теплота.
Работа. Наиболее наглядной формой обмена энергией является механическая работа, соответствующая механической форме движения материи. Она производится при перемещении тела под действием механической силы. В соответствии с другими формами движения материи различают и другие виды работы: электрическую, химическую и т.д. Работа является формой передачи упорядоченного, организованного движения, так как при совершении работы частицы тела движутся организованно в одном направлении. Например, совершение работы при расширении газа. Молекулы газа, находящегося в цилиндре под поршнем, находятся в хаотическом, неупорядоченном движении. Когда же газ начнет перемещать поршень, то есть совершать механическую работу, на беспорядочное движение молекул газа будет накладываться организованное движение: все молекулы получают некоторое смещение в направлении движения поршня. Электрическая работа так же связана с организованным движением в определенном направлении заряженных частиц материи.
Поскольку, работа является мерой передаваемой энергии, количество ее измеряется в тех же единицах, что и энергия.
Теплота. Форму обмена энергией, соответствующую хаотическому движению микрочастиц, составляющих систему, называют теплообменом, а количество энергии, переданное при теплообмене, называют теплотой.
Теплообмен не связан с изменением положения тел, составляющих термодинамическую систему, и состоит в непосредственной передаче энергии молекулами одного тела молекулам другого при их контакте.
П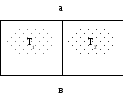 
редставим себе изолированный сосуд (систему) разделенную на две части теплопроводной перегородкой ав (рис. 1.5). Допустим, что в обеих частях сосуда находится газ.
Т1
Рис. 1.5. К понятию о теплоте
В левой половине сосуда температура газа Т1, а в правой Т2. Если Т1> Т2, то средняя кинетическая энергия (
) молекул газа в левой части сосуда, будет больше средней кинетической энергии (
) в правой половине сосуда.
В результате непрерывных соударений молекул о перегородку в левой половине сосуда часть энергии их передается молекулам перегородки. Молекулы же газа, находящегося в правой половине сосуда, сталкиваясь с перегородкой, приобретут какую-то часть энергии от ее молекул.
В результате этих столкновений кинетическая энергия молекул в левой половине сосуда будет уменьшаться, а в правой – увеличиваться; температуры Т1и Т2будут выравниваться.
Поскольку теплота является метой энергии, ее количество измеряется в тех же единицах, что энергия. Таким образом, теплообмен и работа являются формами обмена энергией, а количество теплоты и количество работы - мерами передаваемой энергии. Различие между ними состоит в том, что теплота – это форма передачи микрофизического, неупорядоченного движения частиц (и, соответственно, энергии этого движения), а работа представляет собой форму передачи энергии упорядоченного, организованного движения материи.
Иногда говорят: теплота (или работа) подводится или отводится от системы, при этом следует понимать, что подводиться и отводится не теплота и работа, а энергия, поэтому следует не употреблять такого рода выражений как «запас теплоты» или «теплота содержится».
Являясь формами обмена энергией (формами взаимодействия) системы с окружающей средой, теплота и работа не могут быть связаны с каким-либо определенным состоянием системы, не могут являться ее свойствами, а, следовательно, и функциями ее состояния. Это означает, что если система проходит из начального состояния (1) в конечное (2) различными путями, то теплота и работа будут иметь разные значения для разных путей перехода (рис. 1.6)
Рис. 1. 6
Конечное количество теплоты и работы обозначают Q и A, а бесконечно малые значения соответственно через δQ и δA. Величины δQ и δA в отличие от dU не являются полным дифференциалом, т.к. Q и A не являются функциями состояния.
Когда же путь процесса буде предопределен, работа и теплота приобретут свойства функций состояния системы, т.е. их численные значения будут определяться только начальным и конечным состояниями системы.
39.Энтальпия.Энтальпия образования химических соединений
Для расчетов тепловых эффектов используют величину, называемую энтальпией.
Энтальпией (теплотой) образования химического соединения ∆ HT называется изменение энтальпии в процессе получения 1 моля этого соединения из простых веществ (элементов) при постоянном давлении.
Так, например, энтальпией образования этилового спирта C2H5OH называется изменение энтальпии при реакции углерода, кислорода и водорода при постоянном давлении
2C + 3H2 + 1/2 O2→ CH3 - CH2 - OH
И наоборот, реакции
CH2 = CH2+H2O→CH3 - CH2 - OH
CH3 - CHO+H2→CH3 - CH2 – OH
не являются реакциями ”образования” спирта, хотя и приводят к синтезу этилового спирта.
Важным термодинамическим представлением является понятие о стандартном состоянии вещества, под которым понимается его реальное состояние при 298 К и атмосферном давлении (или p = 101 кПа).
Стандартной энтальпией (теплотой) образования химического соединения 
называется изменение энтальпии в процессе образования 1 моля этого соединения, находящегося в стандартном состоянии, из простых веществ, также находящихся в стандартных состояниях и термодинамически устойчивых при данной температуре фазах и модификациях.
Стандартные энтальпии образования простых веществ принимают равными нулю, если их агрегатные состояния и модификации устойчивы при стандартных условиях.
Стандартная энтальпия образования соединения – мера его термодинамической устойчивости, прочности, количественное выражение энергетических свойств соединения. Если стандартная энтальпия образования отрицательна, то соединение более устойчиво, чем элементы, из которых оно состоит, или наоборот, если она положительна, то соединение менее устойчиво. Из различных молекул более устойчивы те, энтальпии, образования которых меньше.
Например, этан (∆ H298 = - 24,82 ккал/моль) более устойчив, чем этилен 
Термохимические расчеты. Значения энтальпий образования позволяет определить изменения энтальпии, сопровождающие реакции, не прибегая к прямым измерениям.
В основе большинства термохимических расчетов лежит следствие из закона Гесса:
Тепловой эффект химической реакции равен сумме теплот (энтальпий) образования продуктов реакции за вычетом суммы теплот (энтальпий) образования исходных веществ.
Так, для уравнения вида
aA + bB +…= dD + eE +…
Тепловой эффект ∆ H определяется равенством
=
При этом следует иметь в виду, что при алгебраическом суммировании следует учитывать стехиометрические коэффициенты в уравнении реакции (а, в, d, e).
Приведенное уравнение позволяет определять как тепловой эффект реакции по известным энтальпиям образования веществ, участвующих в реакции, так и одну из энтальпий образования, если известны тепловой эффект реакции и все остальные энтальпии образования.
В настоящее время энтальпии образования известны примерно для четырех тысяч веществ, и это позволяет расчётным путем установить тепловые эффекты самых разнообразных реакций.
Пример 1. Расчет теплового эффекта реакции по стандартным энтальпиям образования веществ.
Al2O3 (к) +3SO3 (г) = Al2(SO4)3 (к)
=-1675 кДж/моль; 
=-395, 2 кДж/моль
=-3434 кДж/моль
Тепловой эффект реакции 
определяется по уравнению:
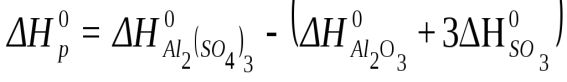
После подстановки значений стандартных энтальпий
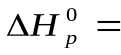-3434-(-1675-3.395, 2)=-599 кДж/моль
Видно, что 
< 0, т.е. это реакция экзотермическая.
Пример 2. Расчет энтальпии образования химического соединения по известному тепловому эффекту реакции.
Определить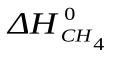 
в реакции:
CH4 (г) + 2 H2O (г) = CO2 (г) + 4 H2 (г)
=-241,82 кДж/моль; 
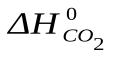=-393,51 кДж/моль; 
= +164,98 кДж
Стандартный тепловой эффект реакции равен:
, откуда
После подстановки стандартных энтальпий образования веществ:
(-1 моль∙ 393,51 кДж/моль + 2 моль ∙ - 241,82 кДж/моль – 164,98 кДж) / 1 моль = - 74,85 кДж/моль
Видно, что реакция образования метана является экзотермической.
Пример 3. Расчет теплового эффекта реакции, который экспериментально определить невозможно.
Реакция 1) C + O2 = CO2, 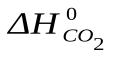= -396 кДж/моль
может быть также осуществлена в две стадии
2) C + 1/2 O2 = CO, 
= -110, 5 кДж/моль
3) CO + 1/2 O2 = CO2
Тепловой эффект реакции 2) можно провести экспериментально и определить = -110, 5 кДж/моль.
А вот тепловой эффект реакции 3) экспериментально осуществить и определить невозможно, поэтому 
реакции 3) получают расчетным путем, используя закон Гесса
- 396 - (-110, 5) = - 285,5 кДж/моль
С помощью термохимических расчетов можно определить энергию химических связей, энергии кристаллических решеток, теплоты растворения и гидратации, тепловые эффекты фазовых превращений и т.д.
Энтальпия есть возрастающая функция температуры, непрерывная во всей области изменения последней, когда существует данная фаза. Для расчета теплового эффекта при температурах, более высоких, чем стандартные, используют уравнение Кирхгофа:
где 
- стандартный тепловой эффект реакции при T = 298 К;
- стандартный тепловой эффект реакции при T.
разность молярных изобарных теплоемкостей всех продуктов реакции и молярных изобарных теплоемкостей всех исходных веществ, т.е.
Расчеты по уравнению Кирхгофа показывают, что в том интервале температур, который может иметь практическое значение, изменение величины теплового эффекта реакции невелико.
Так, например, тепловой эффект процесса 1/2 N2 + 1/2 O2 = NO (г) при повышении температуры от 298 до 4000К изменяется всего лишь на 2,0 кДж/моль. Еще меньше влияние давления на тепловой эффект реакции. Так, для реакции синтеза аммиака из азота и водорода различие между величинами 
при p = 101 кПа и p = 50 МПа не превышает 5 %.
40.Энтропия
Термодинамическая энтропия S, часто просто именуемая энтропия, в химии и термодинамике является функцией состояния термодинамической системы.
Понятие энтропии было впервые введено в 1865 году Рудольфом Клаузиусом. Он определил изменение энтропии термодинамической системы при обратимом процессе как отношение общего количества тепла 
к величинеабсолютной температуры 
:
.
Например, при температуре 0 °C, вода может находиться в жидком состоянии и при незначительном внешнем воздействии начинает быстро превращаться в лед, выделяя при этом некоторое количество теплоты. При этом температура вещества так и остается 0 °C. Изменяется состояние вещества, сопровождающееся выделением тепла, вследствие изменения структуры.
Рудольф Клаузиус дал величине 
имя «энтропия», происходящее от греческого слова τρoπή, «изменение» (изменение, превращение, преобразование). Данное равенство относится к изменению энтропии, не определяя полностью саму энтропию.
Эта формула применима только для изотермического процесса (происходящего при постоянной температуре). Её обобщение на случай произвольногоквазистатического процесса выглядит так:
,
где 
— приращение (дифференциал) энтропии некоторой системы, а 
— бесконечно малое количество теплоты, полученное этой системой.
Необходимо обратить внимание на то, что рассматриваемое термодинамическое определение применимо только к квазистатическим процессам (состоящим из непрерывно следующих друг за другом состояний равновесия).
Поскольку энтропия является функцией состояния, в левой части равенства стоит её полный дифференциал. Напротив, количество теплоты является функцией процесса, в котором эта теплота была передана, поэтому считать полным дифференциалом нельзя.
Энтропия, таким образом, согласно вышеописанному, определена вплоть до произвольной аддитивной постоянной. Третье начало термодинамики позволяет определить её точнее: предел величины энтропии равновесной системы при стремлении температуры к абсолютному нулю полагают равным нулю.
Существует мнение, что мы можем смотреть на S и как на меру беспорядка в системе. В определённом смысле это может быть оправдано, потому что мы думаем об «упорядоченных» системах как о системах, имеющих очень малую возможность конфигурирования, а о «беспорядочных» системах как об имеющих очень много возможных состояний. Собственно, это просто переформулированное определение энтропии как числа микросостояний на данное макросостояние.
Рассмотрим, например, распределение молекул идеального газа. В случае идеального газа наиболее вероятным состоянием, соответствующим максимуму энтропии, будет равномерное распределение молекул. При этом реализуется и максимальный «беспорядок», так как при этом будут максимальные возможности конфигурирования.